前回の弱形式編の記事では、下記の初期配置における幾何学的非線形問題の弱形式を導出しました。この記事では先にこの弱形式問題の非線形性が生じる場所について確認します。
$$
\boxed{
\begin{gathered}
\text { Find } \boldsymbol{u} \in \mathcal{V}_{0}, \quad \mathcal{V}_{0}=\left\{\boldsymbol{u} \mid \boldsymbol{u} \in H^{1}\left(\Omega_{0}\right), \boldsymbol{\nabla} \boldsymbol{u} \in L^{\infty}\left(\Omega_{0}\right), \boldsymbol{u}(\boldsymbol{X}, t)=\overline{\boldsymbol{u}}(\boldsymbol{X}, t) \text { for } t \in\left[t_{0}, t_{1}\right], \boldsymbol{X} \in \partial \Omega_{\mathbf{u}}^{0}\right\} \\
0=\int_{\Omega_{0}} \boldsymbol{S}: \delta \boldsymbol{E} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \mathbf{f}_{\boldsymbol{A}}^{0} \cdot \boldsymbol{\eta}^{0} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \quad\left(\forall \boldsymbol{\eta}^{0} \in \mathcal{W}_{0}\right) \\
\mathcal{W}_{0}=\left\{\boldsymbol{\eta}^{0} \mid \boldsymbol{\eta}^{0} \in H^{1}\left(\Omega_{0}\right), \boldsymbol{\eta}^{0}(\boldsymbol{X})=\mathbf{0} \text { for } \boldsymbol{X} \in \partial \Omega_{\mathbf{u}}^{0}\right\} \
\end{gathered}
}
$$

ここで、 $\boldsymbol{S}$ は第 2 Piola－Kirchhoff 応カテンソル、 $\boldsymbol{E}$ は Green－Lagrange ひずみテンソルです。
$$
\boldsymbol{E}=\frac{1}{2}\left(\boldsymbol{F}^{T} \boldsymbol{F}-\boldsymbol{I}\right)
$$

仮想ひずみテンソル $\delta \boldsymbol{E}$ は $\boldsymbol{E}$ の変分となります。
$$
\begin{aligned}
\delta \boldsymbol{E} & =\frac{1}{2}\left(\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)^{T} \boldsymbol{F}+\boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)\right) \\
& =\operatorname{sym}\left(\boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)\right)
\end{aligned}
$$

ここで、 $\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0} \equiv \boldsymbol{\eta}^{0} \otimes \boldsymbol{\nabla}_{0}$ としました。外力は死荷重（変位に追従しない荷重）を仮定すると、非線形性については、内力項の影響のみ考慮すれば良いことになります。そして、材料非線形の影響を除くように$\boldsymbol{S}=\mathbb{C}: \boldsymbol{E}$ を仮定すると、内力項は以下のように書くことができます。
$$
\begin{aligned}
& \int_{\Omega_{0}} \boldsymbol{S}(\boldsymbol{u}): \delta \boldsymbol{E}(\boldsymbol{u}) d V \\
& =\int_{\Omega_{0}}(\mathbb{C}: \boldsymbol{E}(\boldsymbol{u})): \delta \boldsymbol{E}(\boldsymbol{u}) d V \\
& =\int_{\Omega_{0}}\left(\mathbb{C}: \frac{1}{2}\left(\boldsymbol{F}(\boldsymbol{u})^{T} \boldsymbol{F}(\boldsymbol{u})-\boldsymbol{I}\right)\right): \operatorname{sym}\left(\boldsymbol{F}(\boldsymbol{u})^{T}\left(\nabla_{0} \boldsymbol{\eta}^{0}\right)\right) d V
\end{aligned}
$$
$\boldsymbol{F}$ が変位 $\boldsymbol{u}$ の関数であるため、この内力の弱形式が変位 $\boldsymbol{u}$ の非線形関数となることがわかります。この非線形の弱形式問題を解くためには、線形化の手法がよく使用されます。残差が $R=0$ を満たすように次の線形化手順を繰り返すことになります。
$$
\begin{gathered}
R=\int_{\Omega_{0}} \boldsymbol{S}: \delta \boldsymbol{E} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \mathbf{f}_{A}^{0} \cdot \boldsymbol{\eta}^{0} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V=0 \\ R\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)+\mathrm{DR}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]=0 \quad\left(\forall \boldsymbol{\eta}^{0} \in \mathcal{W}_{0}\right) \\
\boldsymbol{u}_{\text {new }}=\boldsymbol{u}+\Delta \mathbf{u}
\end{gathered}
$$

ここで、 $\mathrm{D} R\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]$ はガト—微分（Gâteaux 微分）
$$
\mathrm{D} R\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]=\left.\frac{\mathrm{d}}{\mathrm{~d} \varepsilon} R\left(\boldsymbol{u}+\varepsilon \Delta \boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)\right|_{\varepsilon=0}
$$

を使用しました（ $\mathrm{DR}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)$ は十分な連続性と有界性を満たすものとします）。この問題の外力は変位の関数ではない（死荷重）ため、 $\mathrm{D} \boldsymbol{R}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]$ を計算するときに外力項を計算しなくても問題ありません。
$$
\begin{aligned}
\mathrm{D} R\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}] & =\mathrm{D}\left(\int_{\Omega_{0}} \boldsymbol{S}(\boldsymbol{u}): \delta \boldsymbol{E}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right) d V\right)[\Delta \mathbf{u}] \\
& =\int_{\Omega_{0}} \mathrm{D} \boldsymbol{S}(\boldsymbol{u})[\Delta \mathbf{u}]: \delta \boldsymbol{E}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right) d V+\int_{\Omega_{0}} \boldsymbol{S}: \mathrm{D} \delta \boldsymbol{E}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}] d V \\
& =\int_{\Omega_{0}}(\mathbb{C}: \mathrm{D} \boldsymbol{E}(\boldsymbol{u})[\Delta \mathbf{u}]): \delta \boldsymbol{E}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right) d V+\int_{\Omega_{0}} \boldsymbol{S}: \mathrm{D}\left(\operatorname{sym}\left(\boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)\right)\right)\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}] d V \\ & =\int_{\Omega_{0}}(\mathbb{C}: \mathrm{D} \boldsymbol{E}(\boldsymbol{u})[\Delta \mathbf{u}]): \operatorname{sym}\left(\boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)\right) d V+\int_{\Omega_{0}} \boldsymbol{S}: \operatorname{sym}\left(\mathrm{D} \boldsymbol{F}^{T}(\boldsymbol{u})[\Delta \mathbf{u}]\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)\right) d V
\end{aligned}
$$

それで、 $\mathrm{D} \boldsymbol{F}(\boldsymbol{u})[\Delta \mathbf{u}]$ と $\mathrm{D} \boldsymbol{E}(\boldsymbol{u})[\Delta \mathbf{u}]$ についてそれぞれ計算すると、
$$
\begin{aligned}
& \mathrm{D} \boldsymbol{F}(\boldsymbol{u})[\Delta \mathbf{u}]=\Delta \mathbf{u} \otimes \nabla_{0} \equiv \nabla_{0} \Delta \mathbf{u} \\
\mathrm{D} \boldsymbol{E}(\boldsymbol{u})[\Delta \mathbf{u}] & =\mathrm{D}\left(\frac{1}{2}\left(\boldsymbol{F}^{T} \boldsymbol{F}-\boldsymbol{I}\right)\right)(\boldsymbol{u})[\Delta \mathbf{u}] \\
& =\frac{1}{2}\left(\mathrm{D}\left(\boldsymbol{F}^{T} \boldsymbol{F}\right)(\boldsymbol{u})[\Delta \mathbf{u}]\right) \\
& =\frac{1}{2}\left(\left(\mathrm{D} \boldsymbol{F}^{T}(\boldsymbol{u})[\Delta \mathbf{u}]\right) \boldsymbol{F}\right)+\frac{1}{2}\left(\boldsymbol{F}^{T} \mathrm{D} \boldsymbol{F}(\boldsymbol{u})[\Delta \mathbf{u}]\right) \\
& =\frac{1}{2}\left(\left(\nabla_{0} \Delta \mathbf{u}\right)^{T} \boldsymbol{F}\right)+\frac{1}{2}\left(\boldsymbol{F}^{T} \nabla_{0} \Delta \mathbf{u}\right) \\
& =\operatorname{sym}\left(\left(\nabla_{0} \Delta \mathbf{u}\right)^{T} \boldsymbol{F}\right)
\end{aligned}
$$

の関係が得られ、これをもとの式に代入すると、$\mathrm{D} \boldsymbol{R}$$(\left.\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]$ が以下のようになります。
$$
\begin{aligned}
\mathrm{DR}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}] & =\int_{\Omega_{0}}\left(\mathbb{C}: \operatorname{sym}\left(\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right)^{T} \boldsymbol{F}\right)\right): \operatorname{sym}\left(\boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)\right) d V+\int_{\Omega_{0}} \boldsymbol{S}: \operatorname{sym}\left(\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)^{T}\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right)\right) d V \\
& =\int_{\Omega_{0}}\left\{\mathbb{C}:\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right)^{T} \boldsymbol{F}\right\}: \boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right) d V+\int_{\Omega_{0}} \boldsymbol{S}:\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)^{T}\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right) d V \\
& =\int_{\Omega_{0}} \boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right):\left\{\mathbb{C}:\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right)^{T} \boldsymbol{F}\right\} d V+\int_{\Omega_{0}} \boldsymbol{S}:\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)^{T}\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right) d V \\
& =\int_{\Omega_{0}}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)^{T} \boldsymbol{F}: \mathbb{C}: \boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right) d V+\int_{\Omega_{0}} \boldsymbol{S}:\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)^{T}\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right) d V \\
& =\int_{\Omega_{0}}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)^{T} \boldsymbol{F}: \mathbb{C}: \boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right) d V+\int_{\Omega_{0}}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right) \boldsymbol{S}:\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right) d V
\end{aligned}
$$

　上式では $\mathbb{C}$ のマイナー対称性 $\left((\mathbb{C})_{i j k l}=(\mathbb{C})_{j i k l}=(\mathbb{C})_{j i l k}=(\mathbb{C})_{i j l k}\right)$ と、$\boldsymbol{S}$ の対称性を利用したため、 $\operatorname{sym}(\cdot)$ を省略することができました。また、 $\boldsymbol{A}:(\boldsymbol{B} \boldsymbol{C})=\operatorname{tr}\left(\boldsymbol{A}^{\boldsymbol{T}} \boldsymbol{B} \boldsymbol{C}\right)=\boldsymbol{B}^{\boldsymbol{T}} \boldsymbol{A}: \boldsymbol{C}$ の関係を使って内積の順序を入れ替え（ $\boldsymbol{A}$ 、 $\boldsymbol{B}$ 、 $\boldsymbol{C}$ が 2 階テンソル）、すこし見やすくなるように変形しました。最終的に、線形化の結果は次の形になりました。
$$
\begin{gathered}
R\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)+\mathrm{D} R\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]=0 \\[2ex]
\\
\begin{aligned}
\mathrm{D} R\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}] &= \int_{\Omega_{0}}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)^{T}(\boldsymbol{F}(\boldsymbol{u})): \mathbb{C}:(\boldsymbol{F}(\boldsymbol{u}))^{T}\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right) d V+\int_{\Omega_{0}}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right) \boldsymbol{S}(\boldsymbol{u}):\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right) d V \\
&= \mathrm{D} R_{\text {Material }}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]+\mathrm{D} R_{\text {Geometry }}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]
\end{aligned} \\[2ex]
\\
\boldsymbol{u}_{\text {new }} = \boldsymbol{u}+\Delta \mathbf{u}
\end{gathered}
$$
$\boldsymbol{u}_{\text {new }}$ が毎回の線形化より得られた変位関数となります。有限要素法を持いた非線形計算では形状関数を用いて離散化した上でこの線形化のプロセスを行うため、実際に計算された結果は全体座標系における各節点上の変位成分となります。つまり、
$$
\left\{\boldsymbol{u}_{\text {new }}\right\}=\left\{{\boldsymbol{u}}\right\}+\left\{{\Delta \mathbf{u}}\right\}
$$

の計算となります。このとき、 $\mathrm{D} R_{\text {Material }}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]$ と $\mathrm{D} R_{\text {Geometry }}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]$ はそれぞれ「材料剛性マトリックス」と「幾何剛性マトリックス」に対応します。幾何剛性 $\mathrm{D} R_{\text {Geometry }}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]$ に応力 $\boldsymbol{S}(\boldsymbol{u})$ が含まれているため、「幾何剛性マトリックス」を評価するため解析中に応力を逐次計算する必要 があります。

　一方、幾何学的非線形を考慮しない微小変形の線形弾性問題を線形化すると、違いがもっと見やすくなります。前回の弱形式編の記事に説明したように、微小変形の弱形式は次のようになります。
$$
\boxed{
\begin{gathered}
\text { Find } \boldsymbol{u} \in \mathcal{V}, \quad \mathcal{V}=\left\{\boldsymbol{u} \mid \boldsymbol{u} \in H^{1}(\Omega), \boldsymbol{u}(\boldsymbol{x}, t)=\overline{\boldsymbol{u}}(\boldsymbol{x}, t) \text { for } t \in\left[t_{0}, t_{1}\right], \boldsymbol{x} \in \partial \Omega_{\mathbf{u}}\right\} \\
\qquad \begin{array}{c}
\displaystyle %
0=\int_{\Omega} \boldsymbol{\sigma}: \boldsymbol{\nabla}^{s} \boldsymbol{\eta} d V-\int_{\partial \Omega_{\mathrm{a}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d S-\int_{\Omega} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d V \quad(\forall \boldsymbol{\eta} \in \mathcal{W}) \\ \mathcal{W}=\left\{\boldsymbol{\eta} \mid \boldsymbol{\eta} \in H^{1}(\Omega), \boldsymbol{\eta}(\boldsymbol{x})=\mathbf{0} \text { for } \boldsymbol{x} \in \partial \Omega_{\mathbf{u}}\right\}
\end{array}
\end{gathered}
}
$$

この弱形式を線形化してみると（ $\boldsymbol{\nabla} \boldsymbol{\eta} \equiv \boldsymbol{\eta} \otimes \boldsymbol{\nabla}$ とします）、
$$
R(\boldsymbol{u} ; \boldsymbol{\eta})+\mathrm{D} R(\boldsymbol{u} ; \boldsymbol{\eta})[\Delta \mathbf{u}]=\mathbf{0}
$$
$$
\begin{aligned}
\mathrm{D} R(\boldsymbol{u} ; \boldsymbol{\eta})[\Delta \mathbf{u}] & =\mathrm{D}\left(\int_{\Omega} \boldsymbol{\sigma}: \boldsymbol{\nabla}^{s} \boldsymbol{\eta} d V-\int_{\partial \Omega_{\mathrm{a}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d S-\int_{\Omega} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d V\right)(\boldsymbol{u} ; \boldsymbol{\eta})[\Delta \mathbf{u}] \\ & =\mathrm{D}\left(\int_{\Omega}(\mathbb{C}: \boldsymbol{\varepsilon}): \boldsymbol{\nabla}^{s} \boldsymbol{\eta} d V\right)(\boldsymbol{u} ; \boldsymbol{\eta})[\Delta \mathbf{u}] \\
& =\int_{\Omega}(\mathbb{C}: \operatorname{sym}(\mathrm{D} \boldsymbol{\nabla} \boldsymbol{u}(\boldsymbol{u} ; \boldsymbol{\eta})[\Delta \mathbf{u}])): \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}) d V \\
& =\int_{\Omega}(\mathbb{C}: \operatorname{sym}(\boldsymbol{\nabla} \Delta \boldsymbol{u})): \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}) d V \\
& =\int_{\Omega} \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}): \mathbb{C}: \operatorname{sym}(\boldsymbol{\nabla} \Delta \boldsymbol{u}) d V \\
& =\mathrm{D} R_{\text {Material }}(\boldsymbol{u} ; \boldsymbol{\eta})[\Delta \mathbf{u}]
\end{aligned}
$$

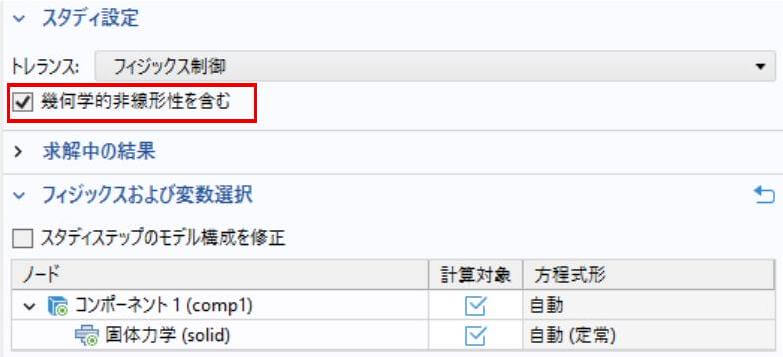
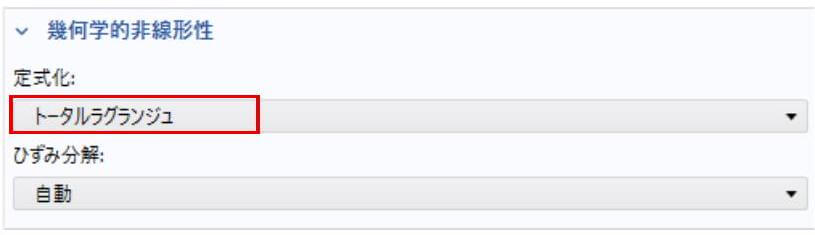
となりました。当然のことですが、この幾何学的線形問題では、幾何剛性が現れない $\mathrm{D} R_{\text {Geometry }}(\boldsymbol{u} ; \boldsymbol{\eta})[\Delta \mathbf{u}]=0$ ことがわかりました。したがって、COMSOL Multiphysics ${ }^{\circledR}$ では図 1 の「幾何学的非線形性を含む」または図 2 の「トータルラグランジアン」を有効にすると、微小変形の場合と比べて、各要素の各積分点において、幾何剛性行列を作成するプロセスが増えるようになります。

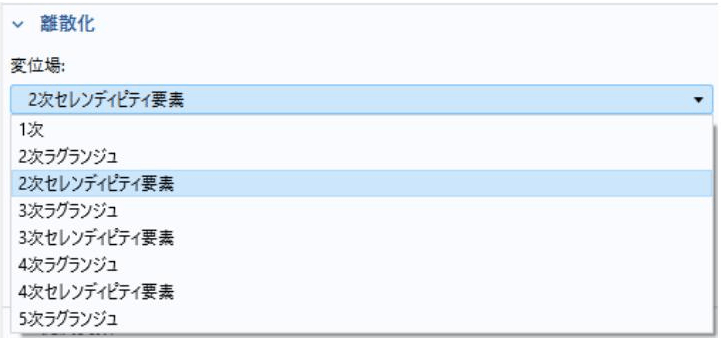
　各積分点で行われる処理は、主に各反復（iteration）の求解計算の準備段階と、変位 $\mathbf{u}$ が得られた後に状態変数を更新する段階で行います。要素数が多いほど、また次数が高いほど、必要なメモリと計算時間は増えます。例えば、図 3 に示すような六面体の 1 次、 2 次、 3 次、 4 次、 5 次ラグランジュ要素は通常それぞれ 8 、 27 、 64 、 125 、 216 個の積分点を持ちます（完全積分を想定する場合）。つまり、要素数が 10 万個前後のモデルに、仮に 5 次ラグランジュ要素を選んだ場合、各反復計算中に要素剛性マトリックスを組み立てるたびに、 $21,600,000$ 個の積分点における離散化された「幾何剛性マトリックス」を評価する必要があります。

　よくある考えとして、幾何学的非線形問題は幾何学的線形問題を含むはずでしょう。または、線形有限要素解析は非線形解析の特例とみなせるでしょう。実際もその通りとなり、例えは幾何学的非線形問題で現れる材料剛性項 $\mathrm{D} R_{\text {Material }}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}]$ を、配置の区別をしないようにする（すなわち $\Omega_{0}= \Omega \Rightarrow \boldsymbol{F}=\boldsymbol{I}$ とみなす）と、幾何学的線形問題に退化することが確認できます。
$$
\begin{aligned}
\mathrm{D} R_{\text {Material }}\left(\boldsymbol{u} ; \boldsymbol{\eta}^{0}\right)[\Delta \mathbf{u}] & =\int_{\Omega_{0}}\left(\boldsymbol{\nabla}_{0} \boldsymbol{\eta}^{0}\right)^{T} \boldsymbol{F}: \mathbb{C}: \boldsymbol{F}^{T}\left(\boldsymbol{\nabla}_{0} \Delta \mathbf{u}\right) d V \\
& =\int_{\Omega}(\boldsymbol{\nabla} \boldsymbol{\eta})^{T} \boldsymbol{I}: \mathbb{C}: \boldsymbol{I}(\boldsymbol{\nabla} \Delta \boldsymbol{u}) d V \\
& =\int_{\Omega} \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}): \mathbb{C}: \operatorname{sym}(\boldsymbol{\nabla} \Delta \boldsymbol{u}) d V \\
& =\mathrm{D} R_{\text {Material }}(\boldsymbol{u} ; \boldsymbol{\eta})[\Delta \mathbf{u}]
\end{aligned}
$$
$R(\boldsymbol{u} ; \boldsymbol{\eta})$ の線形化を完成すると、
$$
\begin{aligned}
0 & =R(\boldsymbol{u} ; \boldsymbol{\eta})+\mathrm{D} R(\boldsymbol{u} ; \boldsymbol{\eta})[\Delta \mathbf{u}] \\
& =\int_{\Omega} \boldsymbol{\sigma}: \boldsymbol{\nabla}^{s} \boldsymbol{\eta} d V-\int_{\partial \Omega_{\mathrm{a}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d S-\int_{\Omega} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d V+\int_{\Omega} \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}): \mathbb{C}: \operatorname{sym}(\boldsymbol{\nabla} \Delta \boldsymbol{u}) d V \\
& =\int_{\Omega}(\mathbb{C}: \boldsymbol{\varepsilon}): \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}) d V-\int_{\partial \Omega_{\mathrm{a}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d S-\int_{\Omega} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d V+\int_{\Omega} \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}): \mathbb{C}: \operatorname{sym}(\boldsymbol{\nabla} \Delta \boldsymbol{u}) d V \\
& =\int_{\Omega} \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}): \mathbb{C}: \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{u}) d V-\int_{\partial \Omega_{\mathrm{a}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d S-\int_{\Omega} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d V+\int_{\Omega} \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}): \mathbb{C}: \operatorname{sym}(\boldsymbol{\nabla} \Delta \boldsymbol{u}) d V \\
& =\int_{\Omega} \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}): \mathbb{C}: \operatorname{sym}(\boldsymbol{\nabla}(\boldsymbol{u}+\Delta \boldsymbol{u})) d V-\int_{\partial \Omega_{\mathrm{a}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d S-\int_{\Omega} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d V
\end{aligned}
$$

となりました。微小変形の弱形式を線形化しても、元と同じ形の弱形式が得られました。つまり、変位 $\boldsymbol{u}$ の大きさに関係なく、 1 回の計算で必要な $\boldsymbol{u}_{n e w}$ を直接求めことができることを意味します。当たり前のことですが、線形解析ではNewton 反復が不要となります。
$$
0=\int_{\Omega} \operatorname{sym}(\boldsymbol{\nabla} \boldsymbol{\eta}): \mathbb{C}: \operatorname{sym}\left(\boldsymbol{\nabla} \boldsymbol{u}_{\text {new }}\right) d V-\int_{\partial \Omega_{\mathrm{a}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d S-\int_{\Omega} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d V
$$

　これまでの内容をまとめると、線形問題と比べ、幾何学的非線形性を考慮した場合に主に増えた計算コストは、Newton 反復、剛性行列の更新と応力計算のことでした：

\begin{gathered} \text{表 1．各種問題の計算コストの比較} \\ \begin{array}{|l|l|l|l|} \hline & \text{幾何学的線形} & \text{幾何学的非線形} & \text{幾何学的線形} \\ & \text{材料線形} & \text{材料線形} & \text{材料非線形} \\ \hline \text{Newton 反復} & \text{不要} & \text{必要} & \text{必要} \\ \hline \text{剛性行列の更新} & \text{不要} & \text{必要} & \text{必要} \\ \hline \text{幾何剛性の計算} & \text{不要} & \text{必要} & \text{不要} \\ \hline \text{応力の保存・更新} & \text{不要} & \text{必要} & \text{必要に応じて} \\ \hline \end{array} \end{gathered}

　幾何学的非線形を考慮しない限り、幾何剛性に関する項が現れることはありません。幾何学的非線形を考慮すると、材料が線形であっても、「材料剛性マトリックス」も変位の関数となります。そして、「幾何剛性マトリックス」を評価するために計算中の応力テンソルの値も必要になります。一方、材料非線形について、仮に材料が弾塑性（材料非線形）を仮定する場合、幾何学的非線形を考慮しなくても、応カ・ひずみ関係が非線形となるため、「材料剛性マトリックス」の更新が発生します。また、応力や内部状態変数の更新も必要となります。幾何学非線形性と材料非線形性の両方を考慮しなければならない計算（例えば、超弾性や超弾塑性）では、計算コストがさらに増えることは容易に想像できます。

著者

張広志 Ph.D.
計測エンジニアリングシステム株式会社 技術部
非線形性固体力学•非線形有限要素法ならびに、COMSOL Multiphysics® への技術サポートに従事
計算力学技術者 固体力学分野1級 振動分野1級