
2 設計プロセスと不確かさの定量化
2.1 設計プロセスと確率モデル
設計プロセスの究極の目的をシンプルに「求められる性能・機能を実現する最適な設計条件を探索すること」と位置付けることができる。設計対象が一つの部品である場合、複数の部品から構成されるユニット、さらには多くのユニットから構成される複雑なシステムというすべての階層において数値化した性能・機能の定量的な評価が求められる。
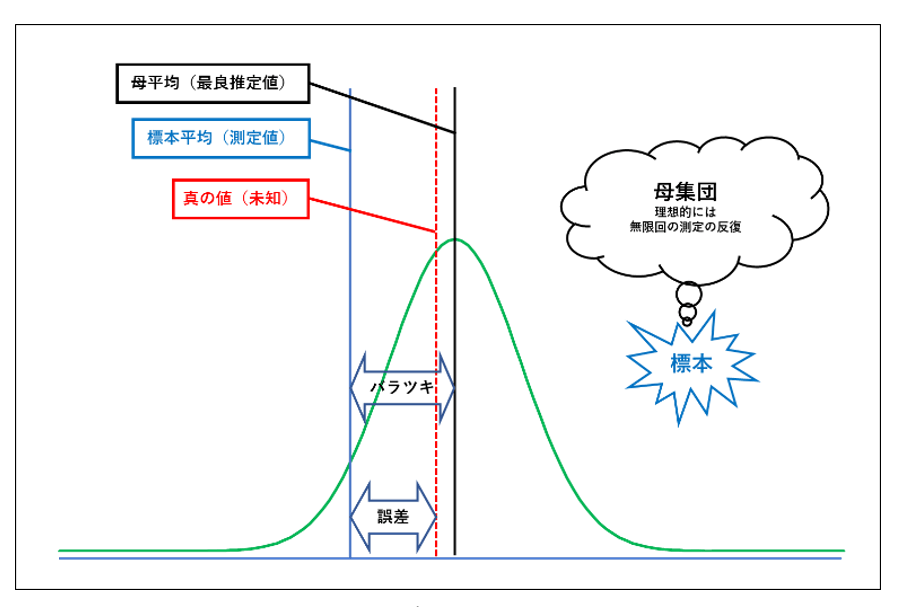
そこで、設計条件に含まれる複数の要因・パラメータと数値化された性能・機能である設計目標との間の因果関係を確率モデルによって表現することを考える(図 2.1参照)。そのためには、設計目標のバラツキの評価に必要となる理想的には無限個の要素から構成される母集団を求める必要があり、以下に説明する対照的な2つのアプローチがある。
2.2 2つのアプローチと確率モデル
実験計画法(Design of Experiments, DOEと略記)によって生成した設計条件に従って試作モデルや縮尺モデルを作成し、その特性を評価することは、モノづくりの分野において従来から行われてきたアプローチである。主成分分析や感度分析などの統計手法を活用することで、設計条件を絞り込む(設計空間を絞り込む)作業を要求される性能・機能が満たされるまで繰り返していた。しかし、設計条件のパラメータが多い場合や試作モデル作成のコスト・時間の制約から、このアプローチには限界があった。
近年のコンピュータの発展に伴い、試作モデルの作成・評価をCAEツールによる仮想実験に置き換えることが可能になり、コスト・時間のハードルは低くなった。しかし、異なる設計条件を網羅的に仮想実験して最適設計条件を求めるようとする、あるいは最適設計条件に対する不確かさ(材料、製造プロセスなどのバラツキ、CAEツールに含まれないパラメータなど)を精査しようとすると、CAEツールのパフォーマンスが新たなハードルとなる。
このハードルを克服するための解決法が以下に説明する代理モデルである。試作モデルや数理モデルから実験結果を得る「演繹」ではなく、実験結果から確率モデルを「帰納」するアプローチである。
2.3 代理モデル
代理モデル(Emulator)とは設計対象の振舞いを表現するモデルであり、設計対象への入力である設計条件 \({\bf X}\) と出力である数値化された性能・機能 \(Y\) との関係を関数 \(Y=f({\bf X})\) として表現するモデルである。CAEツールを活用して代理モデルを生成するプロセスを簡潔に述べると以下の3ステップとなる(図 2.2参照)。
| ステップ1: | DOEにより設計条件の組合せ \({\bf X}\) を生成する |
| ステップ2: | 設計条件ごとにCAEによる仮想実験を繰り返し性能・機能 \(Y\) を評価する |
| ステップ3: | ステップ2で得られた結果を教師データとして学習し、 確率モデルとして最適な入出力関係 \(Y=f({\bf X})\) を求める |
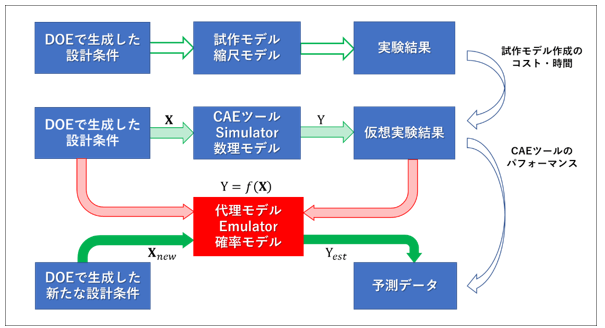
代理モデルの計算負荷は、CAEツールに比べはるかに軽く、新たな設計条件、あるいはより詳細の設計条件である \({\bf X}_{new}\) に対する予測データ \(Y_{est}\) を高速に求めることができる。さらに、予測データは確率モデルから求められるので、より柔軟な設計条件の最適化、感度分析、性能の歩留まりなどを確率的に定量化すること、すなわち不確かさの定量化が可能になる。
設計条件は一般的には高次元のデータであるが、予測データの特性を可視化するために1次元データの場合の例を図 2.3に示す。CAEツールで求めた50組の教師データ(x印)を学習して得られた確率モデルによって求めた予測データの平均値、信頼区間(例えば95%)があたかも連続値のように密に求められている。また、教師データのない区間(グラフの左端および右端)では、信頼区間が大きくなる(バラツキが大きい)ことを読み取ることができる。
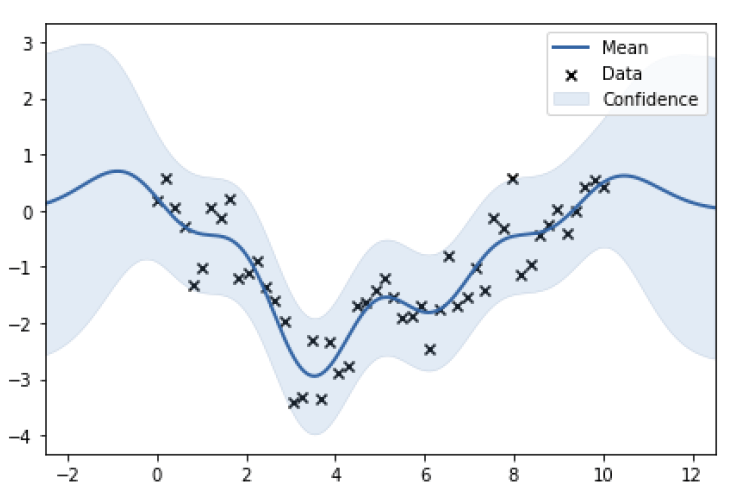
平均値(実線)と信頼区間(網掛け)
次回以降は、確率モデルとして表現される代理モデルを実現するための数学的背景を紹介する。
●モノづくりと不確かさの定量化(第1回)
https://kesco.co.jp/blog/539/