8 ガウス過程回帰のハイパーパラメータ推定

　前回、ガウス過程回帰によって観測値から自由度が高く柔軟な関数の確率モデルが導かれ、複数のテスト入力に対する回帰値とバラツキを表す分散が推定できることを紹介した。
　ガウス過程回帰は、カーネル行列を共分散行列とするガウス分布が主役を務めていることも紹介した。そして、カーネル行列を構成するカーネル関数は、ハイパーパラメータをもつ関数でもあった。前回までは、固定したハイパーパラメータによって推定したが、より良い推定を行うためのハイパーパラメータをチューニングすることが求められる。このチューニングをハイパーパラメータ推定という。ここでは、動径基底関数を例に、最適なハイパーパラメータを推定する方法を紹介する。

8.1 尤度関数の最大化

　次式で表すように、３つのハイパーパラメータをまとめて$\mathit{\vartheta }=({\theta }_1,{\theta }_2,{\theta }_3)$とおくと、カーネル関数は$\mathit{\vartheta }$に依存するので、明示的に 　 $$\begin{array}{}\text{(8.1)}& k(\mathbf{x},{\mathbf{x}}^{\prime }|\mathit{\vartheta })={\theta }_1\exp \left(–\frac{|\mathbf{x}-{\mathbf{x}}^{\prime }{|}^2}{{\theta }_2}\right)+{\theta }_3\delta (\mathbf{x},{\mathbf{x}}^{\prime })\end{array}$$ と表すことができる。さらに、このカーネルから計算されるカーネル行列も$\mathit{\vartheta }$に依存することになるので$K_{\mathit{\vartheta }}$と表すこととする。 観測データ$\mathcal{D}=(X,\mathbf{y})$が与えられたときの出力ベクトルの尤度関数は、 $$\begin{array}{rcl}p(\mathbf{y}|X,\mathit{\vartheta })& =& \mathcal{N}(\mathbf{y}|\mathbf{0},K_{\mathit{\vartheta }})\\ \text{(8.2)}& & =& \frac{1}{(2\pi {)}^{N/2}}\frac{1}{|K_{\mathit{\vartheta }}{|}^{1/2}}\exp (-\frac{1}{2}{\mathbf{y}}^{⊺}{K}_{\mathit{\vartheta }}^{-1}\mathbf{y})\end{array}$$ となる。最適なハイパーパラメータ推定は、この尤度関数を最大化する$\mathit{\vartheta }$を求めることと等価であるので、式 (8.2) の対数を取った対数尤度関数$L$の最大化問題を考えることとする。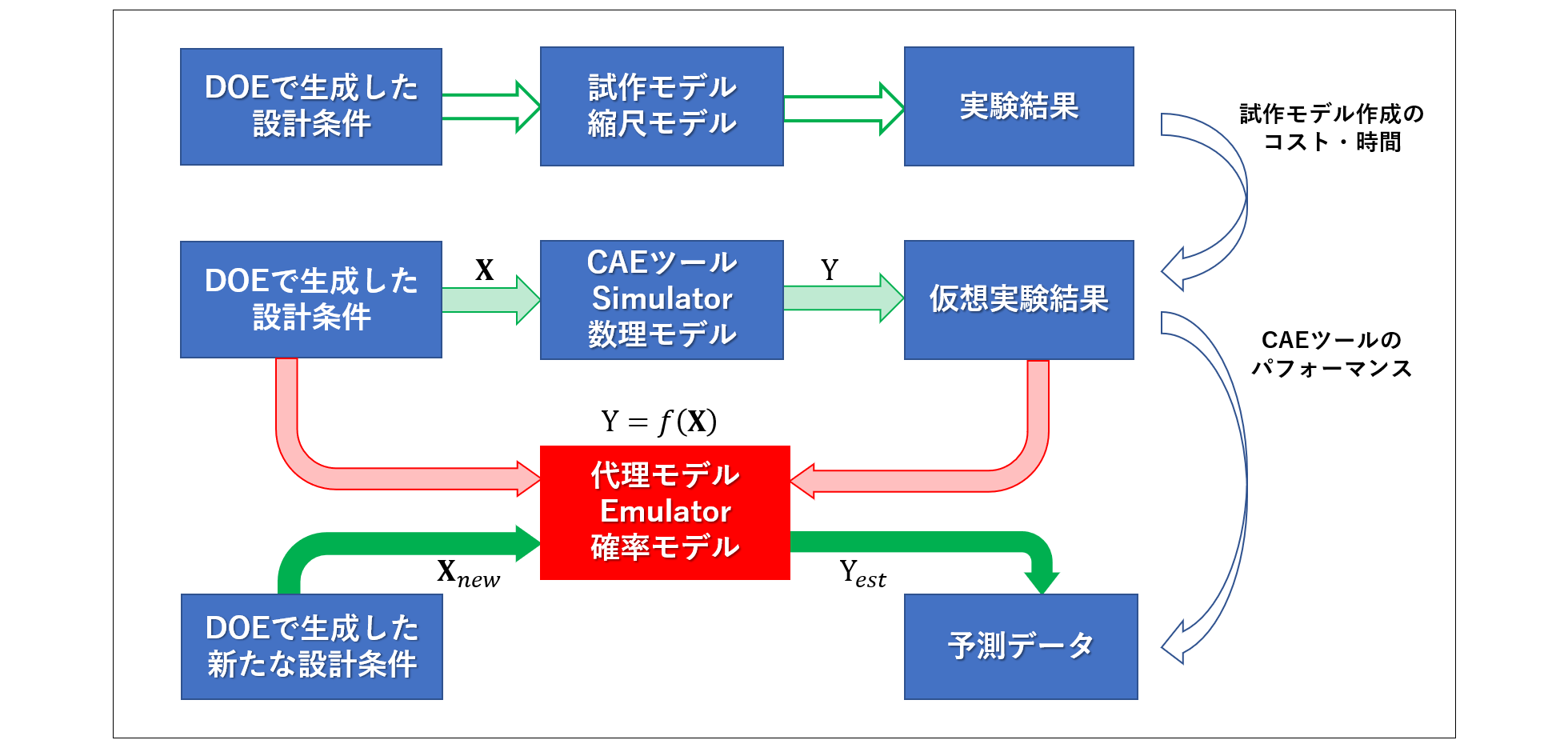　 $$\begin{array}{}\text{(8.3)}& L=\log p(\mathbf{y}|X,\mathit{\vartheta })=-\frac{N}{2}\log (2\pi )-\frac{1}{2}\log |K_{\mathit{\vartheta }}|-\frac{1}{2}{\mathbf{y}}^{⊺}{K}_{\mathit{\vartheta }}^{-1}\mathbf{y}\end{array}$$ 　$\mathcal{D}=\{(-3.5,0.7),(-1.5,1.8),(0,1.6),(0.5,2.3),(3.0,1.0)\}$の5個の観測値が与えられたとき、式 (8.1) のカーネル関数で定義されるガウス過程回帰モデルを考えることとする。ハイパーパラメータを固定した場合と、３つのハイパーパラメータの対数を等間隔$0.025$のグリッド上に配置し、式 (8.3) を直接計算して$L$が最大になるグリッドを推定した場合を比較する。ハイパーパラメータの推定結果は、$\log {\mathit{\vartheta }}_{opt}=(0.400,3.225,-1.950)$で、$L_{max}=-5.9189$であった。図 8.1（左上）に$\log {\theta }_1=0.4$としたときの対数尤度を２次元平面上に等高線図としてプロットした。また、図 8.1（右下）には$\mathit{\vartheta }=(1,1,0.01)$と固定した場合、図 8.1（左下）には${\mathit{\vartheta }}_{opt}$の場合に推定したガウス回帰過程を示した。対数尤度で$3.236$の差（尤度ではおよそ25倍に相当）があることが示された。参考までに、固定したハイパーパラメータ近傍の対数尤度を図 8.1（右上）に示す。

• MCMC法（Markov chain Monte Carlo method, マルコフ連鎖モンテカルロ法）
• SCG法やL-BFGS法などの勾配法（gradient method）

8.2 勾配法

　勾配法は、図 8.1(右上）の青色+を出発点とし、最良推定値である図 8.1（左上）の赤色+である頂上へ辿り着く過程に例えることができる。定性的で直感的ではあるが、出発点における勾配の方向へ進み、峠に到達したら改めて勾配を評価することを繰り返すことで頂上に到達することができる。
　そこで、式 (8.3) で定義する対数尤度の勾配をハイパーパラメータによる微分で評価することを考える。式 (8.3) の係数と定数項を省略した次式を微分する。 　 $$\begin{array}{}\text{(8.4)}& \mathcal{L}=2L=-\log |K_{\mathit{\vartheta }}|-{\mathbf{y}}^{⊺}{K}_{\mathit{\vartheta }}^{-1}\mathbf{y}\end{array}$$ 　式 (8.4) に以下の公式を適用することで、$\mathcal{L}$の$\mathit{\vartheta }$の成分$\theta \in \mathit{\vartheta }$による微分は、

8.3 ガウス過程回帰のまとめ

　ハイパーパラメータ推定については概要のみの紹介となったが、カーネル関数を異なるカーネルの線形結合として定義することもできる。たとえば、線形カーネルとガウスカーネルによって、長期間にわたる気温変動をモデル化することもできる。 $$k(\mathbf{x},{\mathbf{x}}^{\prime }|\mathit{\vartheta })={\theta }_1+{\theta }_2{\mathbf{x}}^{⊺}{\mathbf{x}}^{\prime }+{\theta }_3\exp (-\frac{|\mathbf{x}-{\mathbf{x}}^{\prime }{|}^2}{{\theta }_4})+{\theta }_5\delta (\mathbf{x},{\mathbf{x}}^{\prime })$$ 　これまで線形回帰モデルから出発してガウス過程回帰を紹介してきたが、ガウス過程回帰は「観測値集合から柔軟な回帰モデルの関数$y=f(\mathbf{x})$を推定する確率モデル」と位置付けることができる。
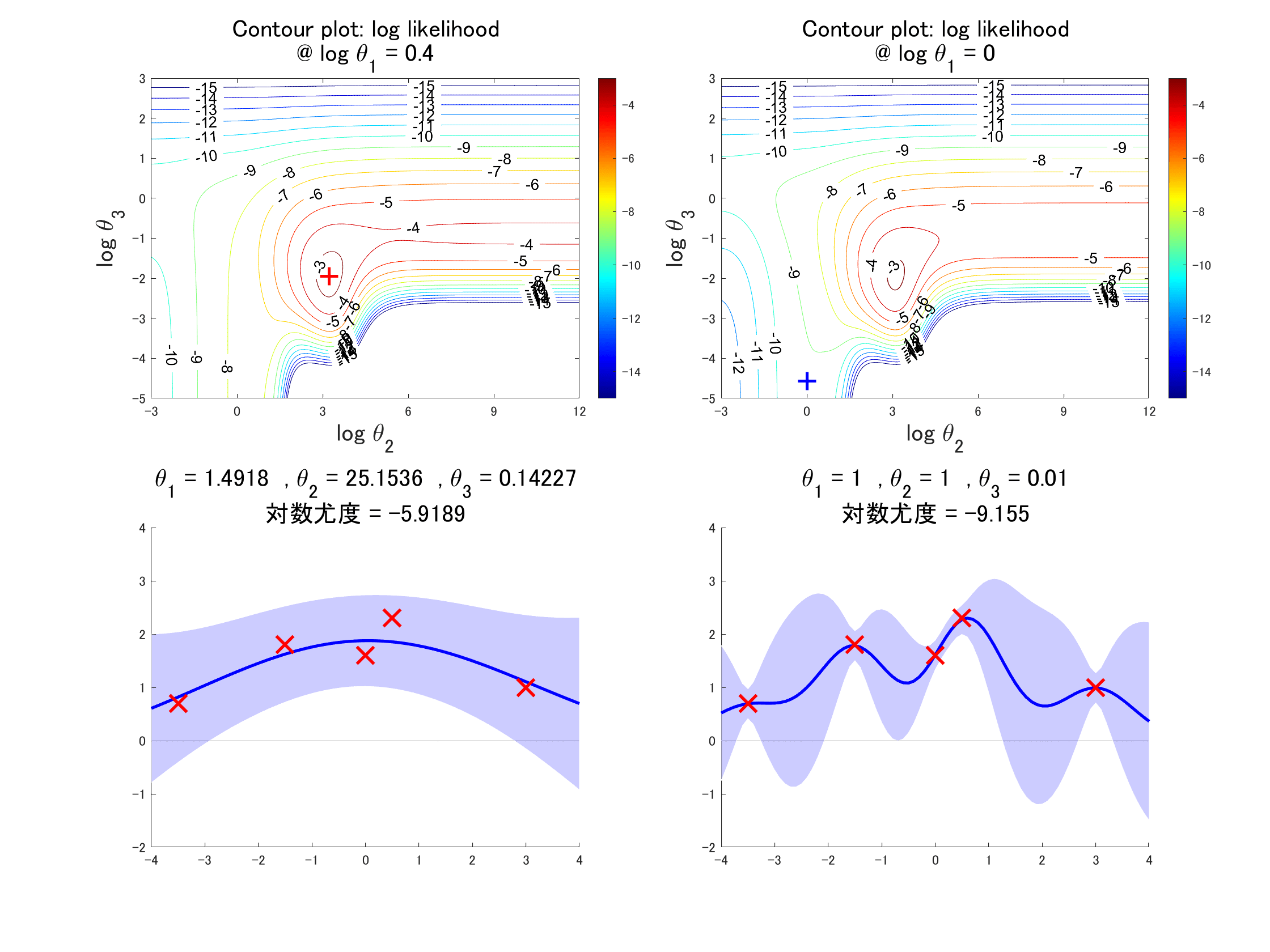
　モノづくりのライフサイクルにおいて、設計プロセスは「性能・品質・コスト」を決定する重要なプロセスである。図 8.2 に示すようにCAEツールと連携することで、部品・アセンブリ・システムそれぞれの階層において試作モデルを作成することなく、「性能・品質・コスト」のバラツキを予測することができる強力なツールを入手したことになる。
　ガウス過程回帰を実装した代理モデル（Emulator）をより効果的に運用するためには、以下の課題が残されている。

• 設計空間が３次元を超える場合のバラツキを可視化するツール
• 効率的な設計条件を探索する実験計画法（design of experiments, DOE）