
1 はじめに
1.1 誤差とバラツキ
モノづくりのプロセスを俯瞰すると、最も単純な部品であれ、多数の部品で構成される複雑なシステムであれ、設計プロセスにおいて「モノ」の仕様である公差(tolerance)が定められる。例えば、鉄の棒の長さは「100.0±0.1cm」のように規定される。一方、生産プロセスでは公差情報に基づいてモノづくりを行い、鉄の棒の長さを測定すると、真の値との差である誤差(error)が発生する。あるいは、鉄の棒の長さにはバラツキ(variation, dispersion)が発生しているとも考えることができる。それでは、誤差とバラツキは違う概念なのでしょうか? さらには、以下に紹介する測定の不確かさ(uncertainty)とは、どのような概念なのでしょうか?
1.2 測定の不確かさとは
2006年に制定されたJIS Z 8404-1では、不確かさを以下のように定めている。
| 3.12 不確かさ(Uncertainty) 測定結果に付随した,合理的に測定対象量に結び付けられ得る値のばらつきを特徴付けるパラメータ (注記1) このパラメータは,例えば,標準偏差(又はそのある倍数)であっても、又は信頼の水準を明示した区間の半分の値であってもよい。 (注記2) 測定の不確かさは一般に多くの成分を含む。これらの成分の一部は一連の測定結果の統計分布によって推定することができ、また、実験標準偏差によって特徴付けられる。その他の成分は,それらもまた標準偏差によって特徴付けられるが、経験又は他の情報に基づいて確率分布を想定して評価する。 (注記3) 測定結果は測定対象量の値の最良推定値であること、並びに補正及び参照標準に付随する成分のような系統効果によって生じる成分も含めた全ての不確かさの成分は、ばらつきに寄与することを考えている |
この定義により、測定結果(測定対象量)は確率モデルで表現されること、明示はされてはいないものの、真の値は未知(あるいは測定により正確に求めることができない)であることが示唆される。
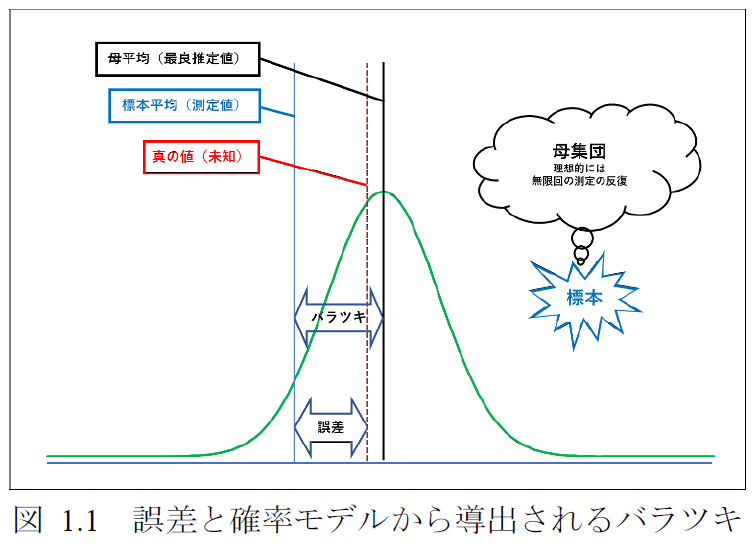
図 1.1に示すように、理想的には無限回の測定の反復で得られる測定結果を要素とする母集団から有限個の標本を抽出することが測定に対応する。母集団の母平均を真の値の最良推定値と考え、母平均と標本平均の差(バラツキ)が不確かさと定義される。前述のJISの引用(注記2)で述べられているように、測定の不確かさは確率変数と見做せる複数の要因(成分)から計算によって合成することができる(詳細は省略)。
1.3 不確かさの定量化
それでは、不確かさの定量化(Uncertainty Quantification, UQと略記)とはどのような概念でしょうか? 前節で述べたように、不確かさは、確率変数と見做せる複数の要因から計算によって合成することができるとした。すなわち、図 1.1の母集団を生成する確率モデルが存在することを示唆している。UQとは、この確率モデルを構成する要因の特性を推定することである。観察した結果から法則や事実を推論する帰納モデル(inductive model)と位置付けられる。
具体的な適用事例として、生産プロセスにおいては、不確かさを生成する要因の特性を定量的に評価し、公差要求を満足することのできない不適合事象を合理的に(不具合ゼロではない)削減することがある。それでは、設計プロセスにおいては、UQがプロセスの効率化、ひいてはモノづくりの効率化にどのように役立つのでしょうか? 次回以降、設計プロセスに焦点をあてて、UQの意義とそれを実現するための確率モデルについて紹介する。