10 ガウス過程の計算パッケージ
ガウス過程は、回帰問題のみならず分類問題や機械学習など多くの分野への応用が可能であり、個別の問題に対応するために、有償あるいは無償の各種計算パッケージの利用が可能になっている。代表的な有償のパッケージは、Mathworks社のMATLAB用のStatistics and Machine Learning Toolboxである。ここでは、無償のパッケージとしてMATLAB用に開発されたGPMLとPythonベースのGPyを紹介する。プログラムの例として第8回のブログで採用した動径基底関数に観測ノイズが重畳した以下のガウス過程回帰モデルのハイパーパラメータの最適化問題を取り上げる。
10.1 ガウス過程回帰モデルのハイパーパラメータの最適化問題
5点の観測データ $$\mathcal{D}=\{(-3.5,0.7),(-1.5,1.8),(0,1.6),(0.5,2.3),(3.0,1.0)\}$$ が与えられたとき、次式で表される回帰モデルの対数尤度関数 $L$ を最大化するハイパーパラメータを推定することを考える。 $$ k\left(\mathbf{x}, \mathbf{x}^{\prime} \mid \boldsymbol{\vartheta}\right)=\theta_{1} \exp \left(-\frac{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|^{2}}{\theta_{2}}\right)+\theta_{3} \delta\left(\mathbf{x}, \mathbf{x}^{\prime}\right) $$ \[\tag{10.1}\] \begin{gathered} L=\log p(\mathbf{y} \mid X, \boldsymbol{\vartheta})=-\frac{N}{2} \log (2 \pi)-\frac{1}{2} \log \left|K_{\vartheta}\right|-\frac{1}{2} \mathbf{y}^{\top} K_{\vartheta}^{-1} \mathbf{y} \end{gathered} \[\tag{10.2}\] 第8回のブログでは、3次元のハイパーパラメータ空間内にグリッドを生成し、各グリッドにおける対数尤度を評価し、最大値 $L_{\text {max }}$ を与えるグリッドから最適なハイパーパラメータ $\vartheta_{o p t}$ を求めた。その結果は $$\vartheta_{o p t}=(1.4918,25.1536,0.14227) 、 L_{\text {max }}=-5.9189$$ であった。この結果から推定した事後分布の信頼区間95%に相当する ${\mu \pm 2 \sigma}$ の領域を図 10.1 (左)に示し、 $\boldsymbol{\vartheta}=(1,1,0.01)$ のときの信頼区間を図 10.1 (右)示す。
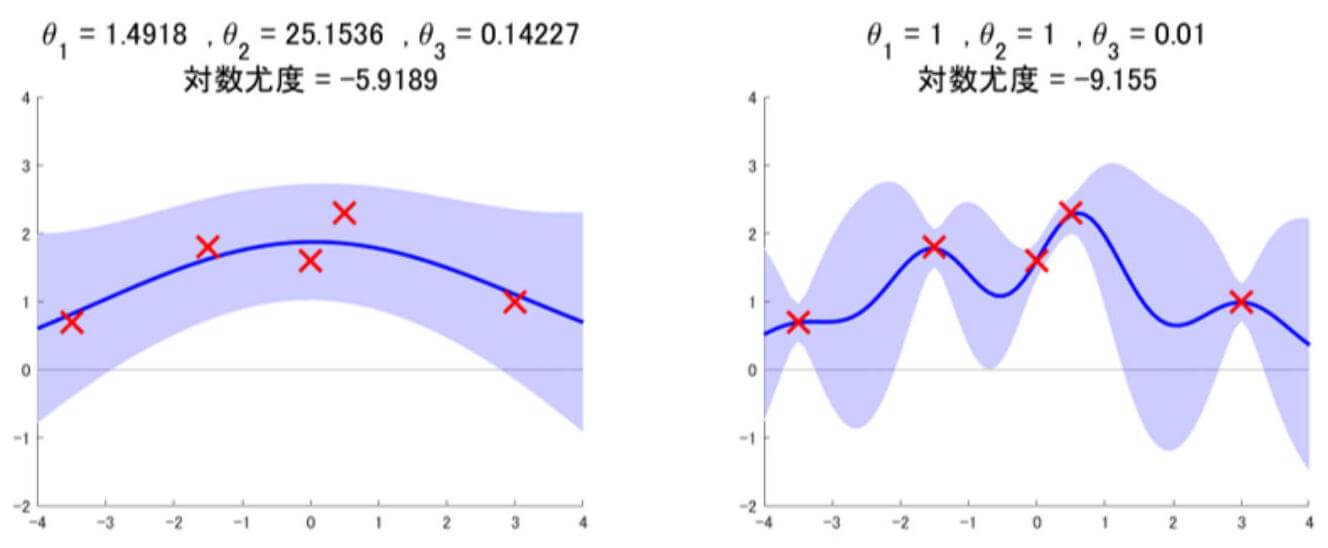
以下、式 (10.1) のハイパーパラメータを、RBFについては信号の分散 $\sigma_{f}^{2}$ と特性長スケールと、ガウスノイズについては分散 $\sigma_{n}^{2}$ としてGPMLとGPyを紹介する。
$$ k\left(\mathbf{x}, \mathbf{x}^{\prime} \mid \boldsymbol{\vartheta}\right)=\sigma_{f}^{2} \exp \left(-\frac{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|^{2}}{2 \ell^{2}}\right)+\sigma_{n}^{2} \delta\left(\mathbf{x}, \mathbf{x}^{\prime}\right) $$ \[\tag{10.3}\]10.2 GPML
Rasmussen C.E.とWiliams C.K.I.による名著「Gaussian Process for Machine Learning」に従つて開発されたMATLAB用の計算パッケージである(無償のOctaveでも利用できるとされている)。ドキュメントを含む計算パッケージはこちらからダウンロードすることができる。 10.1 で設定した回帰問題を解くための主役は、gp関数とminimize関数、そして回帰モデルを定義するための4つの関数オブジェクトと1つのメソッドである。

10.2.1 ガウス過程モデルの定義
ガウス過程を特徴付ける平均値関数と共分散関数そして尤度関数によってガウス過程のモデルが定義される。これらの関数のハイパーパラメータは構造体配列(struct)によって自由に設定することができる。図 10.2 のスクリプトの例では、
- 5行目 : 3つの関数を選択している。具体的には、
・平均値関数は使用しないので空ベクトルを指定
・共分散関数はパッケージで用意されている関数群から式 (10.1) に現れるRBF関数
・尤度関数はやはり用意されている関数群からガウシアン尤度関数
をそれぞれ選択している。 - 6行目 : ハイパーパラメータ $\ell , \sigma_{f} , \sigma_{n}$ の対数を構造体配列 hyp として定義している。
10.2.2 gp関数
10.2.1 で定義されたガウス過程と観測値データ集合から事後分布の推論を行うための関数が gp である。引数として推論メソッドをパッケージで用意されているメソッドから選択するが、図 10.2 では infGaussLik メソッドによってガウス過程回帰による推論を行う。
- 8行目:3つの関数、1つのメソッド、ハイパーパラメータに加え、観測値データ x と y を 引数としている場合には、関数の出力として式 (10.2) の符号を反転した負の対数尤度 (negative log likelihood, NLL) が求められる。
- 9行目:8行目の例に加え、テスト入力が引数として指定されている場合には、関数の出力としてテスト入力点におけるガウス過程モデルの平均値と分散が求められる。
10.2.3 minimize関数
ガウス過程モデルと観測データ集合から負の対数尤度を最小化する最適なハイパーパラメータを共役勾配法(conjugate gradient method)によって推定する。
- 12行目 : 第3引数によって最大反復回数を指定する(この例では100回)。最適化されたハイパーパラメータの構造体配列が関数の出力として求められる。
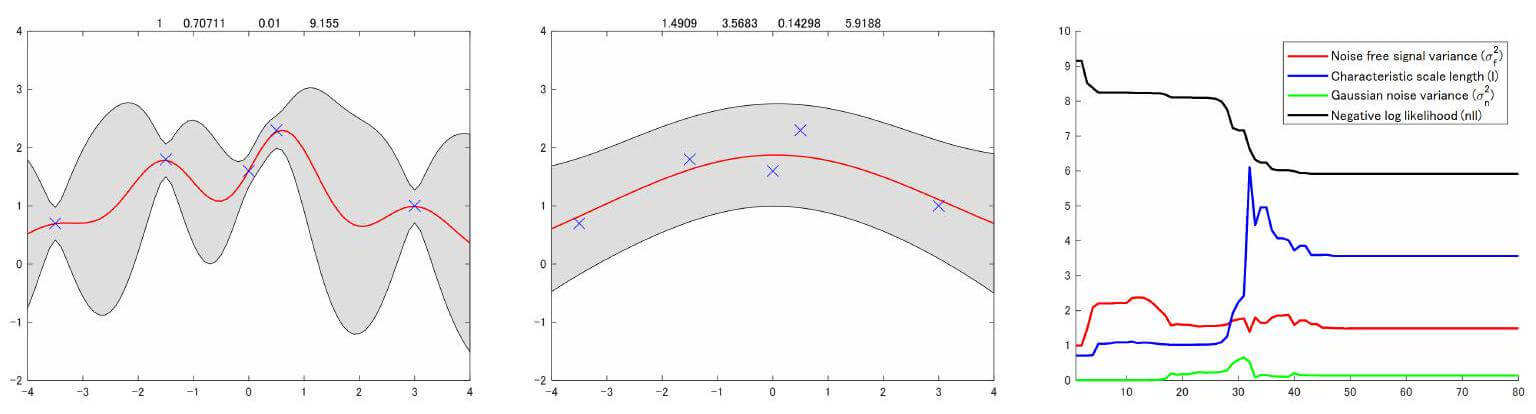
10.2.4 GPMLと直接法との比較
図 10.1 と図 10.3 を比較すると、最適化前はよく一致しているが、最適化後では直接法の区間の両端で信頼区間がわずかに大きくなっていることが分かる。この差は、2つの方法よって推定した $\sigma_{f}^{2}$ のわずかな差(1.4918と1.4909)に起因している。
10.2.5 GPMLのその他の利用方法
GPMLは、ガウス過程モデルに関する各種に問題に対して利用することができ、カーネル関数を定義する平均値関数と共分散関数の選択にも自由度がある。また、回帰モデルのみならず分類モデルに適用でき、尤度関数と推論メソッドの組み合わせによってモデルの事後モデルの解析することができる。例えば、likErf 関数と infEP メソッドの組み合わせによって2クラスのガウス回帰分類モデルを構成することができる。詳細の情報はマニュアルに具体的に示されている。
10.3 GPy
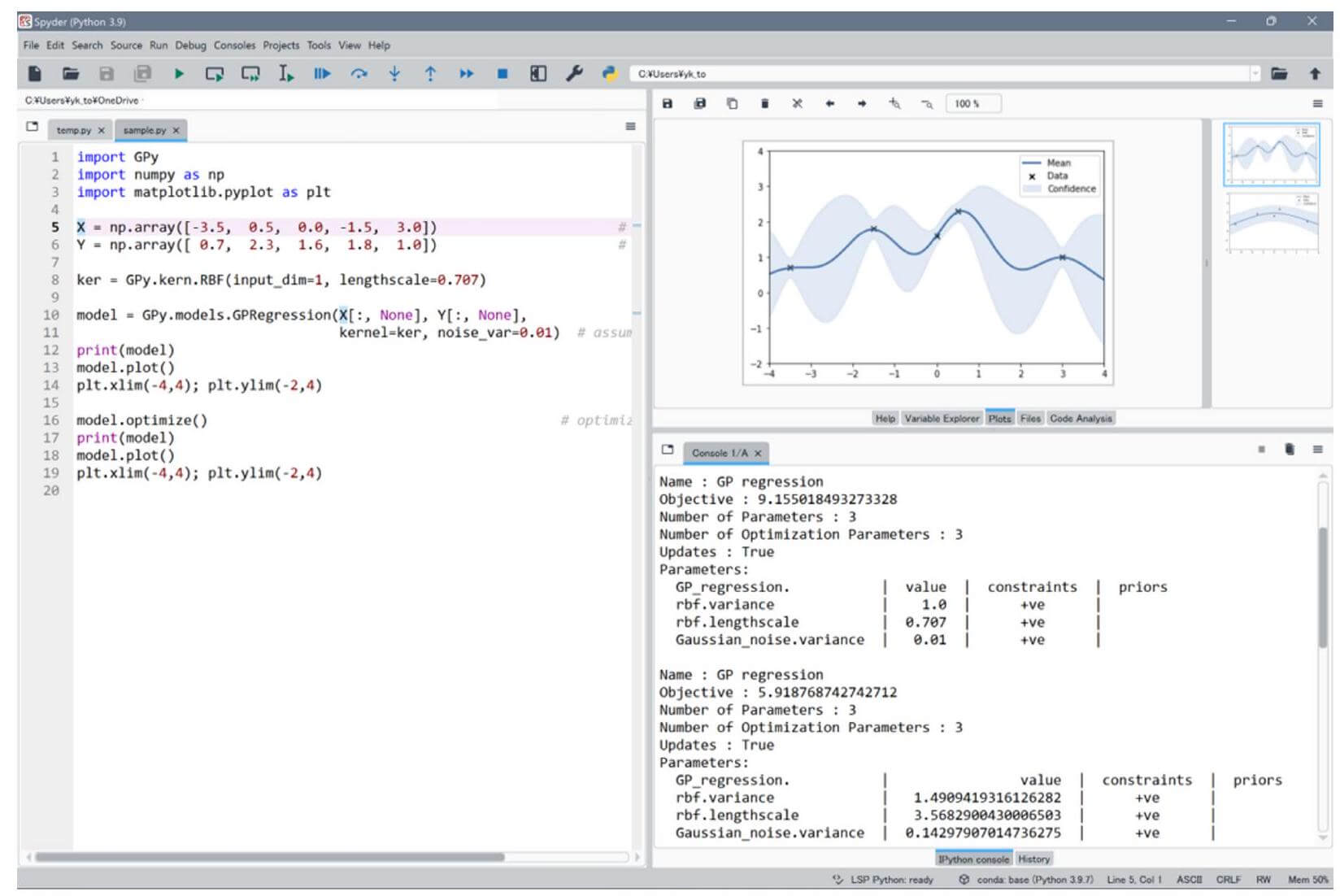
科学計算パッケージPythonの無料ディストリビューションであるAnacondaを使用して 10.1 の問題を解くためのスクリプトを紹介する。Anacondaには、Spyderとよばれる統合開発環境(図 10.4)が同梱されていてインタラクティブなスクリプトの編集・実行ができる。
また、ガウス過程に関する代表的なフレームワークであるGPyは、こちらからダウンロードすることができる。
10.3.1 GPyの構造
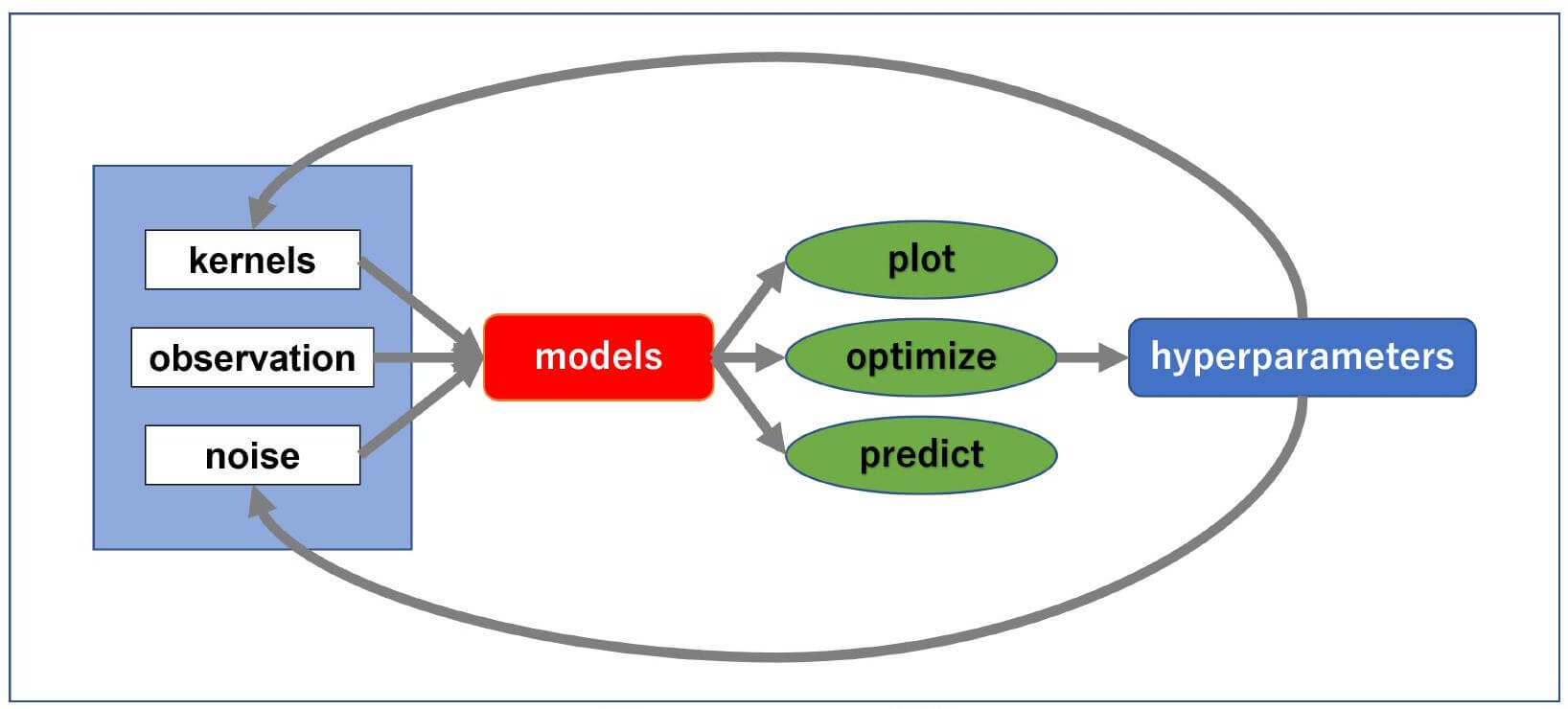
ガウス過程モデルを利用するユーザの視点から見たGPyの構造を図 10.5 に示す。中核となるのが赤色で示すガウス過程モデルであり、カーネル関数、観測値、観測値に重畳するノイズがガウス過程モデルへの入力となっている。GPMLでは中心となる唯一のgp関数の引数として推論メソッドや尤度関数などを関数として明示的に記述していた。一方、GPyではこれらの関数をラップした目的別の関数がそれぞれ用意されいる。また、カーネル関数、観測値、ノイズとガウス過程モデルから定義されたオブジェクトに対するメソッドとして、緑色で示すグラフ作成、ハイパーパラメータの最適化、事後分布の推定などが実装されている。
10.3.2 GPyによるガウス過程回帰モデルのハイパーパラメータ最適化
10.1で示した最適化問題を解くGPyのスクリプトを図 10.6 に示す。
- 8行目 : カーネル関数としてRBF関数を指定すると共に、その引数によつて観測値の次元が1次元、特性長スクール $\ell=\sqrt{1 / 2}$ を指定している。
- 10,11行目 : 観測値データ、8行目で定義したカーネルおよびノイズの分散 $\sigma_{n}^{2}=0.01$ を指定してガウス過程回帰モデルのオブジェクトmodelを定義している。
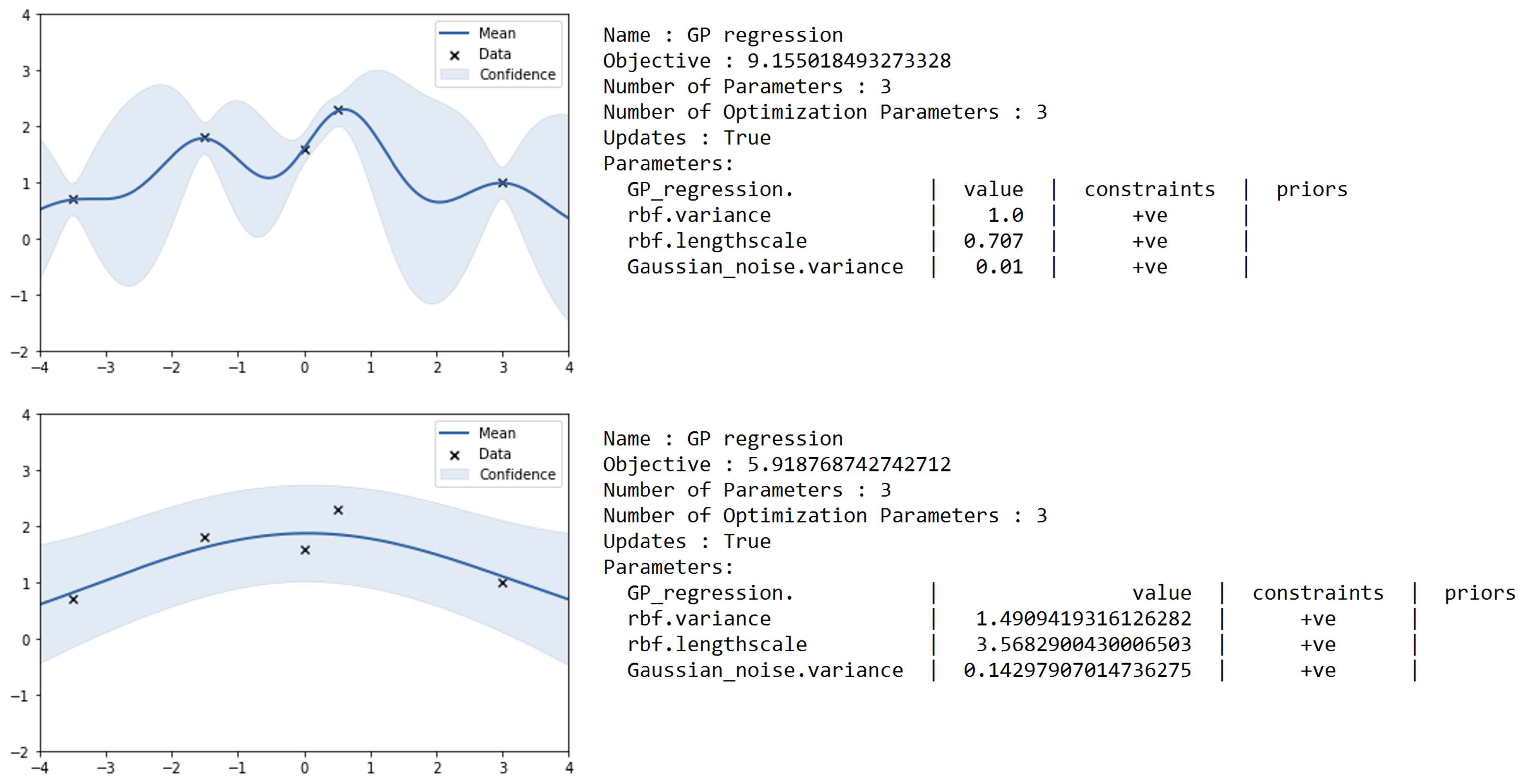
- 12行目 : 定義されたオブジェクトmodelのパラメータをSpiderのConsoleに表示する(図 10.7 の右上)。NLLがパラメータObjectiveとして求められていると共に、信号の分散 $\sigma_{f}^{2}=1$ が選択(8行目の定義の際のデフォルト処理)されていることが分かる。また、制約条件が ‘+ve’ と表示されているのは、パラメータは正の実数であることを示している。
- 13行目 : modelの事後分布の平均値と信頼区間(95%)の領域を表示(図 10.7 の左 上)。
- 16-18行目 : modelを構成する3つのハイパーパラメータを最適化する。その結果は、図 10.7 の下に示す。

10.3.3 GPyの特徴
図 10.6 のスクリプトは、図 10.3 (GPMLによる最適化) と図 10.7 (GPyによる最適化) を比 較するために示したものである。GPyによってガウス過程回帰モデルの事後分布を推定するだけ であれば、図 10.8 のスクリプトの7行目と9行目で十分であり、図 10.7 と同じ結果を得ること ができる。
7行目では、観測値のみを引数として指定しているが、デフォルト値として、
- カーネル関数をRBF関数 (1次元データで信号振幅 $\sigma_{f}^{2}=1$ 、特性長スケール $\ell=1$ )
- ノイズの分散 $\sigma_{n}^{2}=1$
同様に、あらゆる関数には引数が指定されない場合、最大公約数的なデフォルト値が定められていて、ラッパーによる関数の実装と相まって上記の例のように簡潔なスクリプト記述が可能となっている。例えば、 plot()関数にもresolution=200、lower=2.5、upper=97.5といつたデフォルト値が設定されているので、200点のテスト入カ点における信頼区間95%の領域がプロットされる。

10.4 まとめ
簡単なガウス過程回帰モデルを例に、計算パッケージGPMLとGPyの概要を紹介した。2つのパッケージ共に共通して以下のように広い応用範囲をサポートしている。
- 回帰モデルのみならず分類モデルへの適用
- 幅広いカーネル関数、尤度関数、推論メソッドのサポート
- 複雑なカーネル関数の定義。例えば、