現在、電気自動車やハイブリッド自動車において、動力源である二次電池としては高エネルギー密度の観点でリチウムイオン電池が最も応用されているが、電池の大型化、用途の多様化が進む流れの中で、高安全化技術の確立は重要な課題である ${ }^{(1)}$ 。リチウムイオン電池の熱虐待試験は業界標準ベンチマークである。新しく設計したセルや電極材料の安全性をテストするため、セルの小さなテストバッチを作成する必要があり、費用も時間もかかる。

リチウムイオン電池の熱暴走は発熱期、燃焼と噴射期、消滅期の3段階に大別される。リチウムイオン電池が熱暴走すると、副反応により大量の熱が発生し、内部材料が急速に分解して、電池の温度が上昇し続ける。副反応には主に次の4つの部分

1. 負極の固体電解質界面（SEI）の分解
2. 負極活物質の分解
3. 正極活物質の分解
4. 電解質の分解

がある。
この例題は、COMSOL MultiphysicsのPDE機能を用いてリチウムイオン電池の熱暴走現象をモデリングする方法を示す。構築したモデルによって、熱虐待試験における角型リチウムイオン電池の熱暴走挙動のシミュレーションを行い、リチウムイオン電池の熱暴走の発生は環境温度に依存することを検討する。

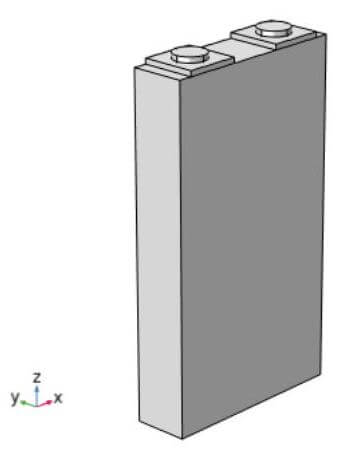
図1にリチウムイオン電池の熱暴走解析モデルを示す。 $3.5 \times 6.2 \times 1 \mathrm{~cm}$ とする角形セルである。正極を $\mathrm{LiCoO}{2}$ 、負極をグラファイトとする。ここでは、 $145 \sim 175^{\circ} \mathrm{C}$ のオーブン温度を扱う ${ }^{(2)}$ 。副反応として4つの分解反応の支配方程式は次式に示される ${ }^{(3)}$. 1）負極の固体電解質界面（SEI）の分解

$$
R{\mathrm{sei}}\left(T, c_{\mathrm{sei}}\right)=A_{\mathrm{sei}} c_{\mathrm{sei}} \exp \left[-\frac{E_{a, \mathrm{sei}}}{R T}\right] \tag{1}
$$
$$
\frac{d c_{\mathrm{sei}}}{d t}=-R_{\mathrm{sei}} \tag{2}
$$
$$
\begin{equation} Q_{\mathrm{sei}}=H_{\mathrm{sei}} W_{c} R_{\mathrm{sei}} \tag{3} \end{equation}
$$

ここで、 $c_{\mathrm{sei}}$ は SEI における Li を含める準安定種の無次元量、 $R_{\mathrm{sei}}、 A_{\mathrm{sei}}、 E_{a, \mathrm{sei}}$ は反応パラメー ター、 $H_{\mathrm{sei}}$ は反応熱、 $W_{c}$ は単位体積当たりの炭素含有量、 $Q_{\mathrm{sei}}$ は熱源である。
2）負極活物質の分解
$$
R_{\mathrm{ne}}\left(T, c_{\mathrm{ne}}, t_{\mathrm{sei}}\right)=A_{\mathrm{ne}} c_{\mathrm{ne}} \exp \left[-\frac{t_{\mathrm{sei}}}{t_{\mathrm{sei}, \mathrm{ref}}}-\frac{E_{a, \mathrm{ne}}}{R T}\right] \tag{4}
$$
$$
\frac{d c_{\mathrm{ne}}}{d t}=-R_{\mathrm{ne}} ; \quad \frac{d t_{\mathrm{sei}}}{d t}=R_{\mathrm{ne}} \tag{5}
$$
$$
Q_{\mathrm{ne}}=H_{\mathrm{ne}} W_{c} R_{\mathrm{ne}} \tag{6}
$$

ここで、 $c_{\mathrm{ne}}$ は炭素内に挿入されたリチウムの無次元量、 $t_{\mathrm{sei}}$ は無次元SEI層の厚さ、 $R_{\mathrm{ne}}, A_{\mathrm{ne}}$ 、 $E_{a, n e}$ は反応パラメーター、 $H_{\mathrm{ne}}$ は反応熱、 $Q_{\mathrm{ne}}$ は熱源である。
3）正極活物質の分解
$$
R_{\mathrm{pe}}(T, \alpha)=A_{\mathrm{pe}} \alpha(1-\alpha) \exp \left[-\frac{E_{a, \mathrm{pe}}}{R T}\right] \tag{7}
$$
$$
\frac{d \alpha}{d t}=R_{\mathrm{pe}} \tag{8}
$$
$$
Q_{\mathrm{pe}}=H_{\mathrm{pe}} W_{p} R_{\mathrm{pe}} \tag{9}
$$

ここで、 $\alpha$ は正極材料の転化率、 $R_{\mathrm{pe}}、 A_{\mathrm{pe}}、 E_{a, \mathrm{pe}}$ は反応パラメーター、 $H_{\mathrm{pe}}$ は反応熱、 $W_{p}$ は単位体積当たりの正極活物質含有量、 $Q_{\mathrm{pe}}$ は熱源である。
4）電解質の分解
$$
R_{\mathrm{e}}\left(T, c_{\mathrm{e}}\right)=A_{\mathrm{e}} c_{\mathrm{e}} \exp \left[-\frac{E_{a, \mathrm{e}}}{R T}\right] \tag{10}
$$
$$
\frac{d c_{\mathrm{e}}}{d t}=-R_{\mathrm{e}} \tag{11}
$$
$$
Q_{\mathrm{e}}=H_{\mathrm{e}} W_{e} R_{\mathrm{e}} \tag{12}
$$

ここで、 $c_{e}$ は無次元の電解質濃度、 $R_{e}, A_{e}, E_{a, e}$ は反応パ ラメーター、 $H_{\mathrm{e}}$ は反応熱、 $W_{e}$ は単位体積当たりの電解質含有量、 $Q_{\mathrm{e}}$ は熱源である。

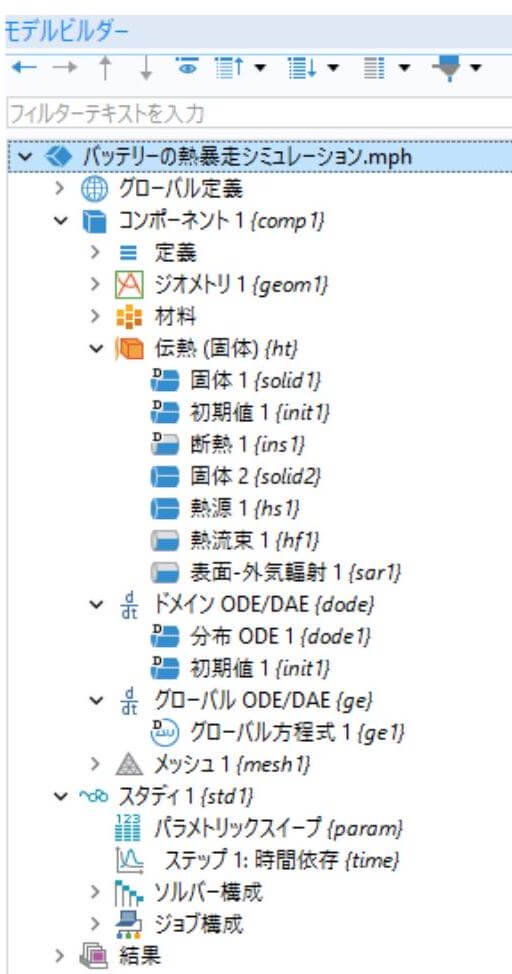
本書では、解析モデルおよび、2章以後に図3の解析結果 を作成する手順を示す。計算用のCOMSOL物理インター フェースを図2に示す。式(1)(2)(4)(5)(7)(8)(10)(11)をドメイ ンODE/DAEインターフェースで解く。熱源Qはグローバル ODE/DAEインターフェースで求められる。ドメイン ODE/DAEとグローバルODE/DAEインターフェースを伝熱 インターフェースと連成してバッテリーの熱暴走シミュレ ーションを行う。

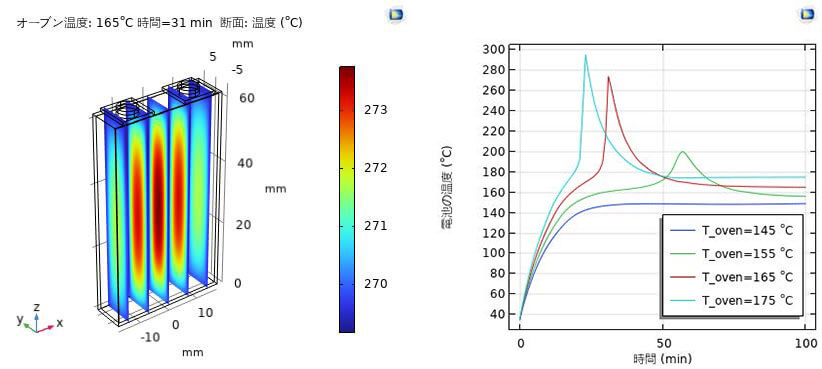
オーブン温度を $165^{\circ} \mathrm{C}$ とした角型リチウムイオン電池内の温度分布と、 $145^{\circ} \mathrm{C}$から$175^{\circ} \mathrm{C}$までのオーブン温度に対して電池セルのコア部の温度は図3に示されている。環境温度$145^{\circ} \mathrm{C}$でのバッテリーは熱暴走しないが、環境温度 $155^{\circ} \mathrm{C}$以上になると、熱暴走が発生することを示した。シミュレーション実験により、リチウムイオン電池は高温環境で使用すると熱暴走の危険性があることを検証した。提示したモデルによって、熱暴走の防止や制御についての研究を助けると期待される。

参考文献

1. 川井友博, 電池の安全性能解析におけるシミュレーション技術の応用, Electrochemistry, vol.78, no. 12, pp. 994-999, 2010.
2. T. D. Hatchard, D. D. MacNeil, A. Basu, and J. R. Dahn, Thermal Model of Cylindrical and Prismatic Lithium-Ion Cells, Journal of the Electrochemical Society, vol. 148, no. 7, pp. A755–A761, 2001.
3. G.H. Kim, A. Pesaran, and R. Spotnitz, A Three-Dimensional Thermal Abuse Model for Lithium-Ion Cells, Journal of Power Sources, vol.170, pp. 476–489, 2007.