現在、電気自動車やハイブリッド自動車において、動力源である二次電池としては高エネルギ一密度の観点でリチウムイオン電池が最も応用されているが、電池の大型化、用途の多様化が進 む流れの中で、高安全化技術の確立は重要な課題である ${ }^{(1)}$ 。リチウムイオン電池の熱虐待試験は業界標準ベンチマークである。新しく設計したセルや電極材料の安全性をテストするため、セル の小さなテストバッチを作成する必要があり、費用も時間もかかる。
サロゲートモデルは代理モデルとも呼ばれ、数値シミュレーション(CAE)の代わりにニュー ラルネットワークなどの機械学習を活用して現象を計算 $\cdot$ 予測する手法のことである。事前に計算したさまざまな条件に対する結果(教師データ)を学習させサロゲートモデルを構築すれば、 CAE計算の工程を省け、複雑なメッシング $\cdot$ 条件設定を一から実行する必要がなくなり、処理時間を短縮できる。
本例題では、18650型 $\mathrm{LiCoO}_{2}$ /グラファイト円筒電池の2Dモデルに基づいて、バッテリーの熱暴走解析のサロゲートモデルを構築する。COMSOLMultiphysics(以下、COMSOLと略称)に実装 された深層学習(DNN、ディープラーニング)手法により熱虐待試験における熱暴走の発生を含 むバッテリー温度の時間変化を予測する。予測結果とCAE計算結果を比較して、サロゲートモデ ルの有効性を検証する。
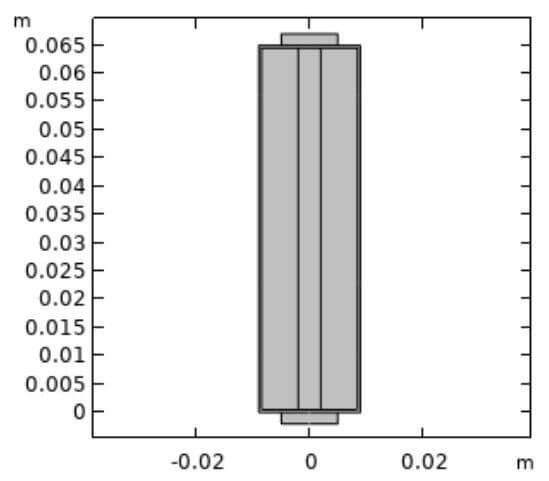
図 1 にバッテリーの熱暴走解析モデルを示す。 $1.8(\mathrm{D}) \times 6.5(\mathrm{H}) \mathrm{cm}$ とする円筒形セルである。正極を $\mathrm{LiCoO}_{2}$ 、負極をグラファイトとする。初期温度は $35^{\circ} \mathrm{C}$ である。バッテリーの熱暴走を引き起こす発熱モデルは以下に 4 つの分解反応によって定義される ${ }^{(2)(3)}$.
1)負極の固体電解質界面(SEI)の分解
$$
R_{\mathrm{sei}}\left(T, c_{\mathrm{sei}}\right)=A_{\mathrm{sei}} c_{\mathrm{sei}} \exp \left[-\frac{E_{a, \mathrm{sei}}}{R T}\right] \tag{1}\
$$
$$
\frac{d c_{\mathrm{sei}}}{d t}=-R_{\mathrm{sei}} \tag{2}
$$
$$
Q_{\mathrm{sei}}=H_{\mathrm{sei}} W_{c} R_{\mathrm{sei}} \tag{3}
$$
ここで、 $c_{\mathrm{sei}}$ は SEI における Li を含める準安定種の無次元量、 $R_{\mathrm{sei}}、 A_{\mathrm{sei}}、 E_{a, \mathrm{sei}}$ は反応パラメー ター、 $H_{\mathrm{sei}}$ は反応熱、 $W_{c}$ は単位体積当たりの炭素含有量、 $Q_{\mathrm{sei}}$ は熱源である。
2)負極活物質の分解
$$
R_{\mathrm{ne}}\left(T, c_{\mathrm{ne}}, t_{\mathrm{sei}}\right)=A_{\mathrm{ne}} c_{\mathrm{ne}} \exp \left[-\frac{t_{\mathrm{sei}}}{t_{\mathrm{sei}, \mathrm{ref}}}-\frac{E_{a, \mathrm{ne}}}{R T}\right] \tag{4}
$$
$$
\frac{d c_{\mathrm{ne}}}{d t}=-R_{\mathrm{ne}} ; \quad \frac{d t_{\mathrm{sei}}}{d t}=R_{\mathrm{ne}} \tag{5}
$$
$$
Q_{\mathrm{ne}}=H_{\mathrm{ne}} W_{c} R_{\mathrm{ne}} \tag{6}
$$
ここで、 $c_{\mathrm{ne}}$ は炭素内に挿入されたリチウムの無次元量、 $t_{\mathrm{sei}}$ は無次元 SEI 層の厚さ、 $R_{\mathrm{ne}}、 A_{\mathrm{ne}}$ 、 $E_{a, \mathrm{ne}}$ は反応パラメーター、 $H_{\mathrm{ne}}$ は反応熱、 $Q_{\mathrm{ne}}$ は熱源である。
3)正極活物質の分解
$$
R_{\mathrm{pe}}(T, \alpha)=A_{\mathrm{pe}} \alpha(1-\alpha) \exp \left[-\frac{E_{a, \mathrm{pe}}}{R T}\right] \tag{7}
$$
$$
\frac{d \alpha}{d t}=R_{\mathrm{pe}} \tag{8}
$$
$$
Q_{\mathrm{pe}}=H_{\mathrm{pe}} W_{p} R_{\mathrm{pe}} \tag{9}
$$
ここで、 $\alpha$ は正極材料の転化率、 $R_{\mathrm{pe}} 、 A_{\mathrm{pe}} 、 E_{a, \mathrm{pe}}$ は反応パラメーター、 $H_{\mathrm{pe}}$ は反応熱、 $W_{p}$ は単位体積当たりの正極活物質含有量、 $Q_{\mathrm{pe}}$ は熱源である。
4)電解質の分解
$$
R_{\mathrm{e}}\left(T, c_{\mathrm{e}}\right)=A_{\mathrm{e}} c_{\mathrm{e}} \exp \left[-\frac{E_{a, \mathrm{e}}}{R T}\right] \tag{10}
$$
$$
\frac{d c_{\mathrm{e}}}{d t}=-R_{\mathrm{e}} \tag{11}
$$
$$
Q_{\mathrm{e}}=H_{\mathrm{e}} W_{e} R_{\mathrm{e}} \tag{12}
$$
ここで、 $c_{e}$ は無次元の電解質濃度、 $R_{e}, A_{e}, E_{a, e}$ は反応パラメーター、 $H_{\mathrm{e}}$ は反応熱、 $W_{e}$ は単位体積当たりの電解質含有量、 $Q_{\mathrm{e}}$ は熱源である。
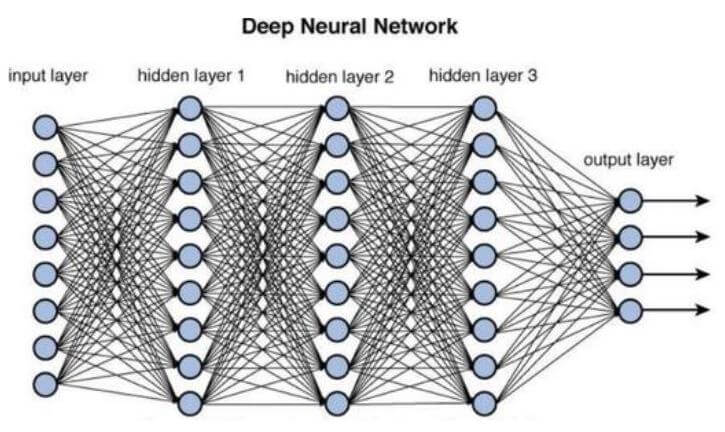
深層学習(DNN)モデルは、入力層、中間層(隠れ層)および出力層で構成される。各層は、多数のノード、つまりニューロンで構成される。図2に5層のニューラルネットワークを示す。
本例題のサロゲートモデルのトレーニングは、COMSOLのパラメトリックスイープを用いた CAE計算からの出力データに基づいている。このパラメトリックスイープを効率的にするには、「実験デザイン」法が使用されるCOMSOLの専用 のサロゲートモデルトレーニングスタディは過度のCAE計算を必要とせずに入力空間を均一に カバーするデータセットを生成するラテン超方格サンプリング(Latin hypercube sampling, LHS)法を採用する。
本書では、解析モデルおよび、解析結果を作成 する手順を示す。
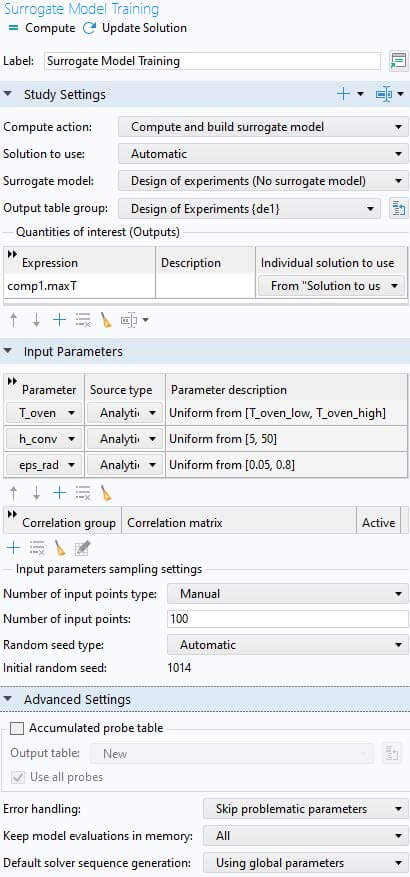
図3はCOMSOL の専用のサロゲートモデルト レーニングスタディの設定画面であり、その中で入力データは熱虐待試験のオーブン温度 (T_oven)、熱伝達率(h_conv)および表面放射率 (eps_rad)、 出力データはバッテリーの最大温度と する。
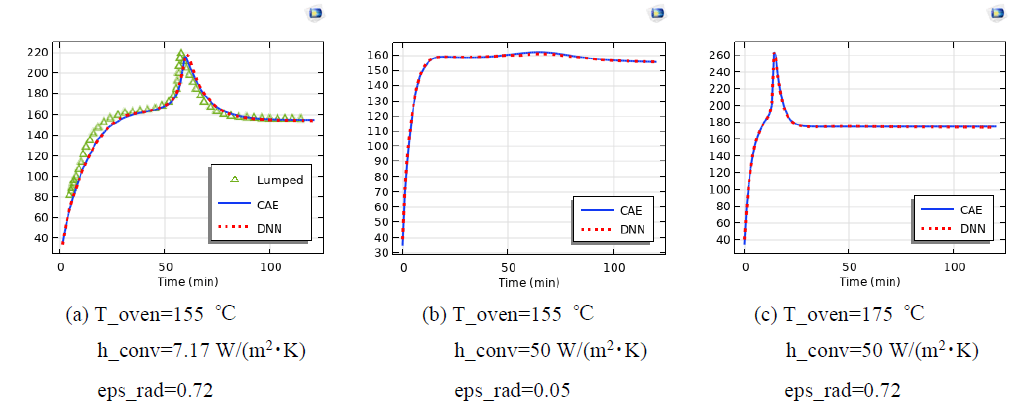
熱虐待試験に対して $145^{\circ} \mathrm{C}$ から $175^{\circ} \mathrm{C}$ までのオ ーブン温度とする教師データをトレーニングし た. $155^{\circ} \mathrm{C}$ と $175^{\circ} \mathrm{C}$ とした予測結果は図 4 に示され ている。 $155^{\circ} \mathrm{C}$ の結果には文献 ${ }^{(2)}$ の集中モデルの計算結果とも比較した。熱伝達率と表面放射率が熱暴走の発生タイミングへの影響を含むバッテリ一の温度は時間が経つにつれて変化することも、 サロゲートモデルによる予測結果がCAE解析結果とよく一致した。
サロゲートモデルによって予測結果を即時反映 することで、リチウムイオン電池が高温環境での応用検証について、サロゲートモデルの活用が期待される。
参考文献
- 川井友博, 電池の安全性能解析におけるシミュレーション技術の応用, Electrochemistry, vol.78, no. 12, pp. 994-999, 2010.
- G.H. Kim, A. Pesaran, and R. Spotnitz, A Three-Dimensional Thermal Abuse Model for Lithium-Ion Cells, Journal of Power Sources, vol.170, pp. 476–489, 2007.
- T. D. Hatchard, D. D. MacNeil, A. Basu, and J. R. Dahn, Thermal Model of Cylindrical and Prismatic Lithium-Ion Cells, Journal of the Electrochemical Society, vol. 148, no. 7, pp. A755–A761, 2001.