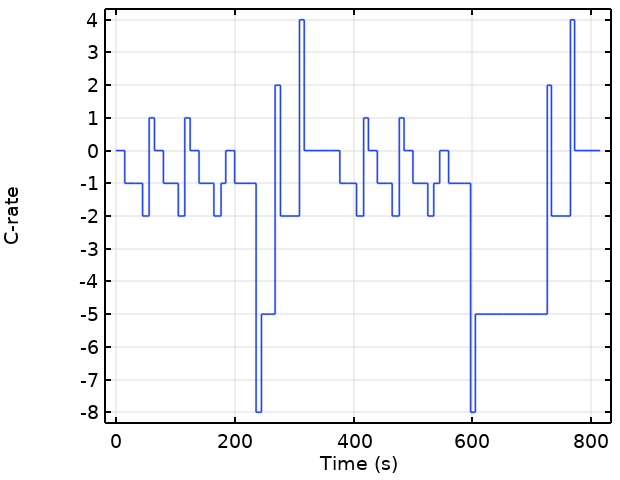
現在，電気自動車やハイブリッド自動車において，動力源である二次電池としては高エネルギー密度の観点でリチウムイオン電池が最も応用されているが，電池の大型化，用途の多様化が進む流れの中で，高安全化技術の確立は重要な課題である． リチウムイオン電池は，充放電を繰り返すことにより劣化（サイクル劣化）するほか，放置することによっても劣化（保存劣化）することから，実車両に搭載されている電池の状態はその使用履歴に依存し，電池寿命を客観的に評価することは困難である．そのため，サイクル劣化，保存劣化を個別に評価する手法が一般的である1)．ここでは，走行時の負荷変動や回生充電を含んだISOのサイクル寿命試験用の放電プロファイル2)を考慮する．図1に電力基準から電流基準に変更された放電プロファイルを示している．

この計算例は，角形リチウムイオン電池の熱分析の3Dモデルを構築する。電池セルにおける オーム抵抗と電荷移動および拡散プロセスに基づく電池のすべての電圧損失を取り扱える COMSOL Multiphysics ${ }^{\circledR}$ の集中電池モデル3）と，集電板，集電箈および端子における電流分布に より発生する熱源を伝熱解析モデルに導入する。図1に示した放電プロファイルに基づいて，自動車業界にとってより現実的なリチウムイオン電池の熱分析を検討する． 本書では解析モデルおよび，解析結果を作成する手順を示した。 計算ジオメトリは，図2に示すような，角形リチウムイオン電池の容量は25 Ahであり，正極 をNMC（ $\mathrm{LiNi}_{1 / 3} \mathrm{Mn}_{1 / 3} \mathrm{Co}_{1 / 3} \mathrm{O}_{2}$ ），負極をグラファイト，電解質を $\mathrm{LiPF}_{6}(\mathrm{EC}: \mathrm{EMC}=3: 7)$ とする ${ }^{2}$ ）. 電池の電圧 $E_{\text {cell }}$ は次式で定義される. $$ E_{\text {cell }}=E_{\text {eq,pos }}\left(\chi_{\text {pos }}, T\right)-E_{\text {eq,neg }}\left(\chi_{\text {neg, }}, T\right)+\eta_{\text {IR }}+\eta_{\text {act,pos }}-\eta_{\text {act,neg }}+\eta_{\text {conc,pos }}-\eta_{\text {conc,neg }} $$ ここで、 $E_{\mathrm{eq}}$ は電極の平衡電位，$\chi$ はリチウム化度，$T$ は温度，$\eta_{\mathrm{IR}}$ ，$\eta_{\mathrm{act}}$ および $\eta_{\mathrm{conc}}$ はそれぞれ抵抗分極，活性化分極および濃度分極である。下付き文字 pos と neg はそれぞれ正極と負極を意味する.

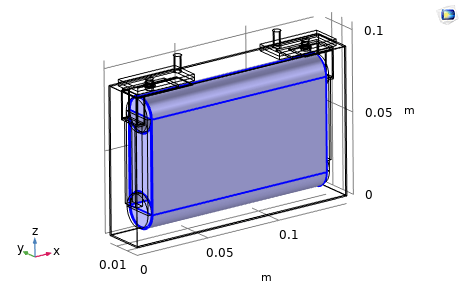
$\chi^{\text {は }} 1 \mathrm{D}$ での無次元変数 $X$ を用いて次の式により得られる. $$ \tau \frac{\partial \chi}{\partial t}=-\nabla \cdot(-\nabla \chi) $$ $\boldsymbol{\tau}$ は拡散時間定数，$t$ は時間である。境界条件は $$ \begin{aligned} & \left.\nabla \chi\right|_{X=0}=0 \\ & \left.\nabla \chi\right|_{X=1}=-\frac{\tau I_{\mathrm{pos} / \mathrm{neg}}}{3 Q_{\mathrm{host}}} \end{aligned} $$ となる．$X=0$ は粒子の中心，$X=1$ は粒子の表面と定義される。 $Q_{\text {host }}$ は電極ホスト容量である.
集電板，集電箔および端子における電流分布は次 の式で求められる. $$ \begin{aligned} & \nabla \cdot \mathbf{i}_{s}=Q_{\mathrm{s}} \\ & \mathbf{i}_{s}=-\sigma_{\mathrm{s}} \nabla \phi_{\mathrm{s}} \end{aligned} $$ ここで， $\mathbf{i}_{S}$ は電流密度，$\phi_{\mathrm{s}}$ は電位，$\sigma_{\mathrm{s}}$ は導電率，$Q_{\mathrm{s}}$ は電流源である.
伝熱解析は以下の熱伝導方程式で計算される. $$ \rho C_{p} \frac{\partial T}{\partial t}+\nabla \cdot \mathbf{q}=Q_{\mathrm{h}} $$ ここで、 $T$ は温度，$\rho$ は密度，$C_{p}$ は熱容量， $\mathbf{q}$ は熱流束，$Q_{\mathrm{h}}$ は熱源である $. \mathbf{q}=-k \nabla T$ と定義され，$k$ は熱伝導度である.
図1に示した放電プロファイルをCOMSOLのイベ ントインターフェースによって導入する．COMSOL の設定画面を図3に示す.

図 4 は放電後 726 s の時のリチウムイオン電池の温度分布および電極端子温度の時間変化である。初期温度は $20^{\circ} \mathrm{C}$ ，初期 SOC （充電状態）は 0.85 であり，電池ケース底部の温度を $20^{\circ} \mathrm{C}$ と設定した.放電において電池の SOC が 0.85 から 0.5 まで減少され，電池の温度は 726 s の時に最大 $27.6^{\circ} \mathrm{C}$ になった.電極端子温度の時間変化は試験結果 ${ }^{1)}$ とおおよそ一致したことが示された.

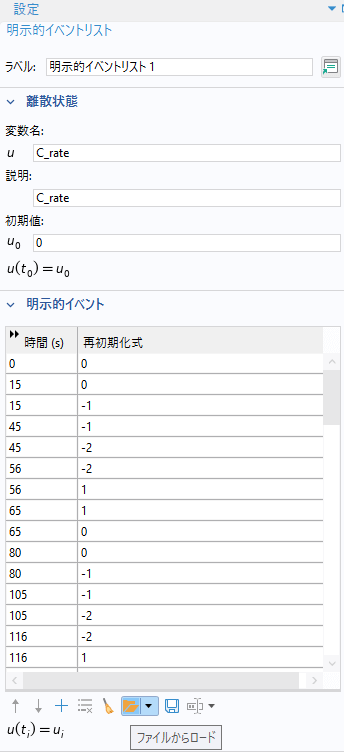
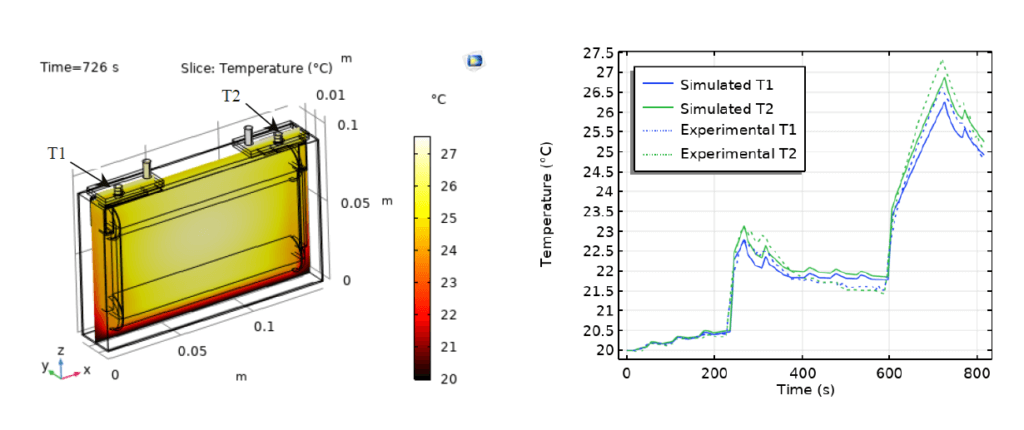
参考文献
1) 松田智行, 安藤慧佑, 明神正雄, 今村 大地, JARI Research Journal, 20171002 (2017).
2) H. Lundgren, P. Svens, H. Ekström, C. Tengstedt, J. Lindström, M. Behm, G. Lindbergh, J. Electrochem. Soc., Vol. 163, No. 2, A309–A317 (2016)
3) 佟立柱，福川真，計算工学 25(4)，4145-4150 (2020)．

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。