めっき,電着塗装などの表面処理は,装飾,防食,表面硬化などを用途として,多くの製品の製造に欠かせない工程である.めっきプロセスにおいて,できるだけ短時間に,しかも均一な膜厚を持つ製品および生産設備を設計することは重要な技術課題となっている.現在,CAE(Computer Aided Engineering:計算機支援工学)は産業界のものづくりの実際の現場に普及しており,また,製品の高機能・高性能化に伴い,試作実験そのものに高度な技術や技能が必要となっており,数値解析でしか評価できない場合も発生する.
近年のPCB 設計では,基板表面である高アスペクト比のスルーホール内部へのめっきの均一性向上のため,めっき溶液に様々な添加剤が使われている.これによって,添加剤が材料の配分を改善するが,展延性と導電性の両方を制限することがあり,従来の直流めっきが限界に達している.また,添加剤は生産コストの重要な部分を占めており,プロセス制御が難しく,廃液処理により環境負荷が高くなる問題がある1).この問題に対して,パルスめっきでは,添加剤を利用せず,高アスペクト比のスルーホールにも非常に優れた材料配分を実現できる.
本研究では,シリコン貫通電極(TSV:Through Silicon Via)の構造を支えるビアフィリング銅めっき技術をパルス電流でモデリングを行う. 図1に示した電流パルスを用いて高アスペクト比であるパルスめっきプロセスの解析を考慮する2).
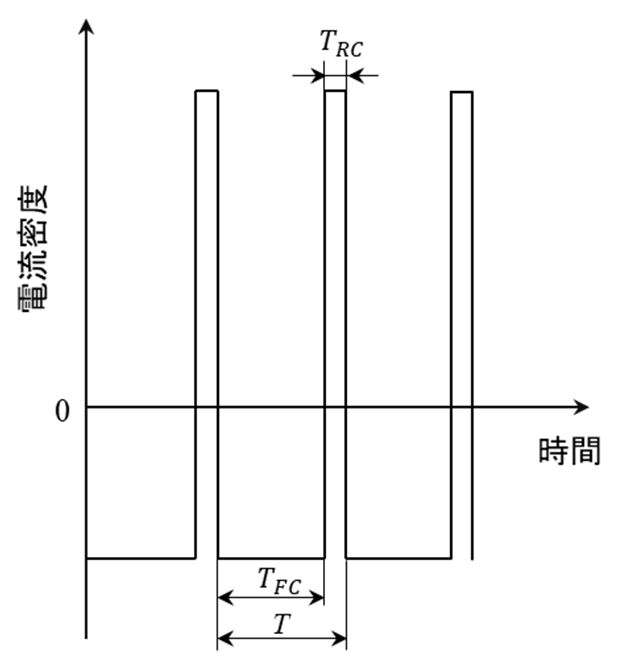
図1 に示すパルス電流密度を次式で示し,COMSOL のイベントインターフェースで実現させる.
$$
i_{\mathrm{PRC}}= \begin{cases}i_{\mathrm{PC}}, & n T \leq t<(n+1) T-T_{\mathrm{RC}} \tag{1}\ i_{\mathrm{RC}}, & (n+1) T-T_{\mathrm{RC}} \leq t<(n+1) T\end{cases}
$$
ここで、 $i_{\mathrm{PRC}}$ はパルス電流密度,$i_{\mathrm{PC}}$ は順方向のパルス電流密度,$i_{\mathrm{RC}}$ は逆方向のパルス電流密度, $T$ はパルスの周期,$T_{\mathrm{FC}}$ は 1 周期内における順方向の電流密度の印加時間,$T_{\mathrm{RC}}$ は 1 周期内におけ る逆方向の電流密度の印加時間,$T=T_{\mathrm{FC}}+T_{\mathrm{RC}}$ である.$n$ をパルス繰り返し数とする.
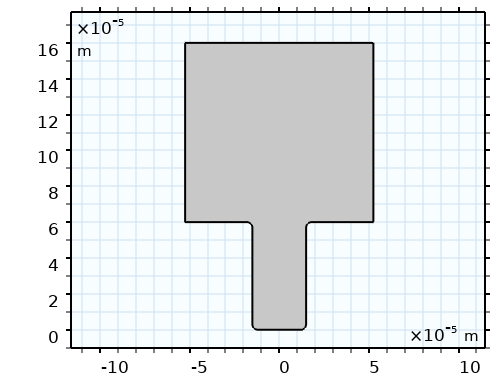
パルスめっきの解析モデル 3)を図 2 に示す。アスペクト比を 2 とする高さ $60 \mu \mathrm{~m}$ ,幅 $30 \mu \mathrm{~m}$ で ある TSV トレンチである.拡散層として $0.3 \mathrm{M} \mathrm{CuSO}_{4}$ 硫酸銅溶液の厚さを $100 \mu \mathrm{~m}$ とする。トレ ンチの上端,拡散層の境界電位を 0 にし,被めっき電極(カソード)にパルス電流を印加するこ とをモデル化する.計算領域を電解質領域とする.
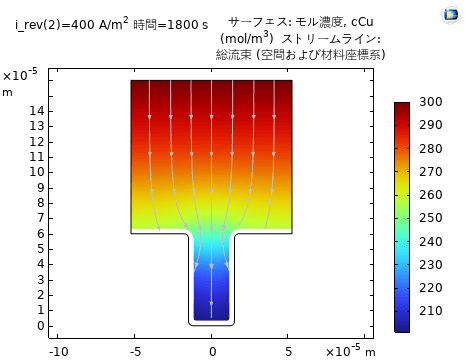
$\mathrm{Cu}^{2+}$ の濃度勾配はカソード反応に導入し, 3 次電流分布を計算する。めっき液における電流分布は以下の式で求められる。 $$ \begin{align*} & \nabla \cdot \mathbf{i}_{l}=0 \tag{2}\\ & \mathbf{i}_{l}=F\left(\sum_{i}\left(-z_{i}\right) D_{i} \nabla c_{i}-\nabla \phi_{l} \sum_{i}\left(z_{i}\right)^{2} u_{m, i} F c_{i}\right) \tag{3} \end{align*} $$
ここで, $\mathbf{i}_{l}$ はめっき液の電流密度,$c_{i}$ は濃度,$D_{i}$ は拡散係数,$z_{i}$ はイオン価数,$u_{m, i}$ はイオンの移動度,$F$ はファラデー定数,$\phi_{l}$ は電位である。カソード表面の電流密度 $i_{\mathrm{loc}}$ は以下のバトラー・ボ ルマーの式で表される。 $$ \begin{equation*} i_{\mathrm{loc}}=i_{0}\left[\exp \left(\frac{\alpha_{a} F}{R T} \eta\right)-\frac{c_{\mathrm{c}}}{c_{\mathrm{b}}} \exp \left(-\frac{\alpha_{c} F}{R T} \eta\right)\right] \tag{4} \end{equation*} $$
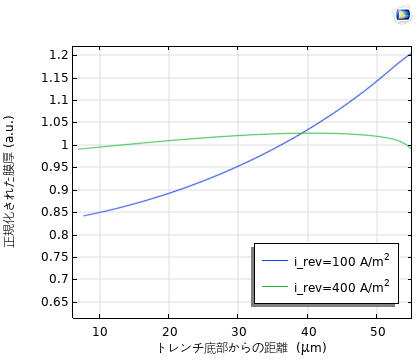
参考⽂献
1) P. Leisner, P. Møller, M. Fredenberg, I. Belov; Trans. IMF., Vol. 85, No. 1, 40 (2007).
2) Y. Dong, B. Jiang, J. Qiang, Z. Ma, D. Drummer, L. Zhang; J. Mater. Res. Technol., Vol. 24, 3055
(2023).
3) 佟 立柱,永山達彦, 表面技術, Vol. 76, No. 3, 135 (2025).
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。