絶縁油などの液体誘電体は，多くの高電圧(HV, High Voltage)電力機器の絶縁材料として利用されている．高電圧環境下に置かれた絶縁油中で発生するストリーマ放電の進展メカニズムや，液体中にある固体絶縁表面上の沿面放電など，さまざまな部分放電現象を解明することは重要である．しかしながら，現在，油紙（油/プレスボード）絶縁の部分放電特性に関する研究は，主に劣化度，温度，電圧振幅，破壊電圧や部分放電開始電圧などの因子について，実験的手法により調査されている．部分放電，特にストリーマ放電進展の完全なメカニズムを理解するには，微視的な電荷輸送に基づいた解析が必要であり，数値解析的な手法が有効である¹⁾．

そこで本例題は図1に示す針―平板電極系におけるストリーマ放電進展シミュレーションを行った．電極間での距離は1 cmである．液体中の放電プロセスは非常に短く，液体内部への進展が数百ナノ秒しかかからない．そのため，放電プロセスはHVサイクルよりもはるかに短い時間で完了する．従って，液体中のストリーマシミュレーションにはDC電圧が適していると考えられる．本モデルでは，HV電極電圧を60 kVに設定した．

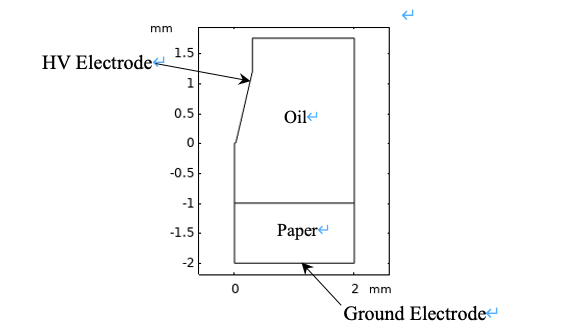
本書ではモデルおよび，図3の解析結果を作成する手順を示す．
ここでは，COMSOL Multiphysicsの電気放電モジュールを用いて，液体および固体誘電体における電荷輸送計算をポアソン方程式と完全に結合させ，絶縁油中のストリーマ放電および油紙絶縁表面上の沿面放電について検討する．
液体誘電体における電荷輸送モデルは，ドリフト拡散モデルとも呼ばれ，液体の電子(e)，正イオン(p)，および負イオン(n)の挙動を解く．

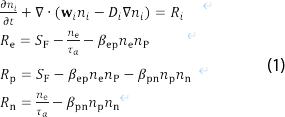
ここで，i = e, p, n はそれぞれ液体中の電荷キャリア，n_i は数密度，w_I はドリフト速度，D_I は拡散係数，R_I は反応速度である． w_i = z_iμ_iE であり，μ_i は移動度，E は電界，z_i はキャリア電荷，z_e,p,n = -1 , 1 , -1 である．τ_αは電子付着時間定数，β_ep と β_pn は電子-イオンとイオン間の再結合係数，S_p は電界イオン化率である．
固体誘電体における電荷輸送モデルはバイポーラ電荷輸送モデルとも呼ばれる．支配方程式は液体誘電体中の電荷輸送方程式と形は同じであるが，固体の電子(e)，正孔(h)，そしてトラップされた電子(te)と正孔(th)の挙動を解く．反応速度 R_i は次の式で定義される．

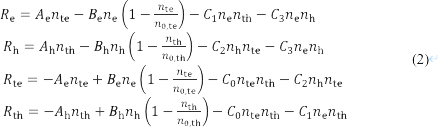
ここで，A_e と A_h は捕獲電子と捕獲ホールの脱出率，B_e と B_h は電子とホールの捕獲率，n_0,te と n_0,th は電子とホールの深い捕獲の数密度，C₀ , C₁ , C₂ , C₃ はそれぞれ捕獲電子と捕獲ホール，電子と捕獲ホール，捕獲電子とホール，電子とホールの再結合係数である．
バイポーラ電荷輸送モデルにおける空間電荷の注入はショットキー法則に従い，注入電流密度 J_in が次の式で計算される．

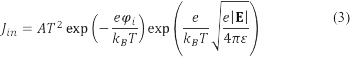
ここで，A はリチャードソン定数，T は温度，κ_Bはボルツマン定数，φ_iはショットキー注入障壁,  i = e, h である．
ポアソン方程式は電荷輸送モデルと完全に結合され, 次の式に示す．

∇・(εE) = ρ

ここで，ρは空間電荷密度，ρ = eΣ_iz_in_i, e は電気素量，ε は誘電率である．誘電界面における電荷輸送は次の式で計算される．

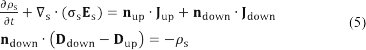
ここで，ρ_s は表面電荷密度，E_s は表面電界，σ_s は表面導電率，D は電束密度，J は電流密度，n は法線ベクトル，下付き文字 down と up は界面と領域の関係を意味する．
計算には絶縁油の物性がCOMSOL電気放電材料ライブラリから導入して, プレスボードの物性は図2に示すパラメーター₂₎によって設定された．220 ns までストリーマ放電進展シミュレーションを行った．計算時間は 19時間34分 である．計算用のパソコンスペックは以下の通りである．

1. OS: WINDOWS 11
2. CPU: Intel® Xeon® Gold 6334 CPU @ 3.60GHz (3.70 GHz)
3. メモリ（RAM）：128 GB

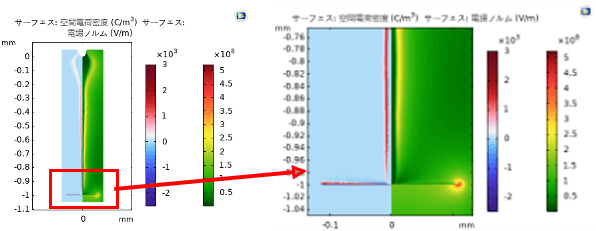
図3は HV 電極電圧を 60 kV とした場合の計算結果である．油中の初期電子・イオン密度は 10⁶ cm^-3，プレスボードにおける電子・ホール密度と捕獲電子・ホール密度の初期値はそれぞれ 0.05 C·m^-3 と 0.01 C·m^-3 ，プレスボードの表面導電率は 10^-16 S·m^-2 とした．図3にストリーマの典型的な放電過程を再現し，ストリーマ発達の先頭に高電界が生成され, 空間電荷が電界分布に与える影響は明確に示唆されている．さらに，ストリーマが油紙界面に到着して，界面に沿って放電を続ける様子が示された．

参考文献

1. D. He, W. Gong, Z. Xu, et al.: Effect of the DC Electric Field Polarity and Amplitude on Partial Discharge of Oil–Paper Insulated under Wedge-shaped Electrodes, IEEE Trans. Dielectr. Electr. Insul., 29 (2022) 599.
2. S. Li, Q. Li and D. He: PD classification in oil-pressboard insulation by simulating a needle-plate model with +DC voltage, IEEE Trans. Dielectr. Electr. Insul., 26 (2019) 261.

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりご請求ください。