金属の腐食は酸化還元反応により表面の金属が電子を失ってイオン化し金属面から溶出する ことで進行する。多くの産業における金属材料の腐食は，金属製品，機器，装置あるいは構造物 の寿命を短縮し，多額の補修•取換費を必要とするので，経済的損失となる。また，金属製品は使用環境や経年によって，さびなどの腐食が生じ，重大な事故災害に直結することがある。

腐食の進行に要する時間は長く，実験により腐食現象をありのままに再現することは困難で ある。また，すきま腐食は，狭小領域で電気化学反応に伴う大きな電流密度で金属が溶解し，溶液組成， pH ，溶存酸素濃度が変化するために，外部の環境と大きく異なってくる。一般的にすき ま間隔は，数十 $\mu \mathrm{m}$ 以下であり，非常に薄く，環境因子の実験的な測定などが行いにくいので，数値解析的な手法が有効となる。しかしながら，すきまの領域では，金属電極表面の電気化学反応，金属イオンの溶液内導電電流，溶液内化学種の輸送など，特に溶液特性変化も関与するため，数値解析モデル化は開発難度が高い。

従来，腐食防食に関わる数値計算においては境界要素法が広く利用されている。この方法によ り溶液中の電位と電流密度及び金属表面の腐食速度を解析することは可能であるが，溶液内の化学種の輸送及び溶液特性変化の計算はできない。塩化ナトリウム（ NaCl ）水溶液中でステンレ ス鋼にすきま腐食が発生する場合，多種の金属イオンが溶出し，沖合いからすきま内部に塩化物 イオン $\mathrm{Cl}^{-}$が侵入する。そのため，溶液特性変化の計算が必要になる。

この計算例は COMSOL Multiphysics ${ }^{\circledR}$ を用いて NaCl 水溶液中の SUS304 ステンレス鋼のすき ま腐食シミュレーションを行った。金属表面の電気化学反応と溶液内の拡散泳動，並びに溶液化学反応を連成させることで、すきまにおける各種イオンおよび酸素濃度の変化，さらには Cl濃度に伴う分極特性変化などを計算に組み込んで実現した。

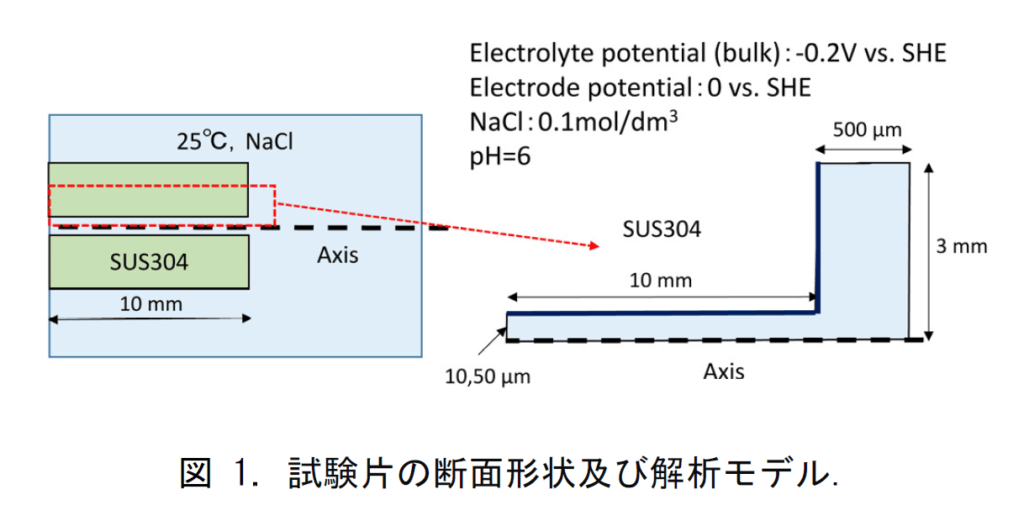
計算ジオメトリは，図 1 に示すような，試験片の断面形状を仮定する。すきま腐食は外部の電位を－0．2V v．s．SHE の定電位に設定する条件で進行させる．COMSOL 計算モデルの組み合わせ は以下の通りである ${ }^{1)}$ 。

1） 3 次電流分布（電気中性）（tcd）および化学（chem）インターフェース

2）考慮した化学種（14 種）： $\mathrm{Fe}^{2+}, \mathrm{Ni}^{2+}, \mathrm{Cr}^{3+}, \mathrm{H}^{+}, \mathrm{OH}^{-}, \mathrm{FeOH}^{+}, \mathrm{CrOH}^{2+}, \mathrm{Na}^{+}, \mathrm{Cl}^{-}$， $\mathrm{FeCl}^{+}, \mathrm{FeCl}{2}, \mathrm{CrCl}^{2+}, \mathrm{O}{2}, \mathrm{H}{2} \mathrm{O}$

3）溶液中の化学反応を表1に示す。

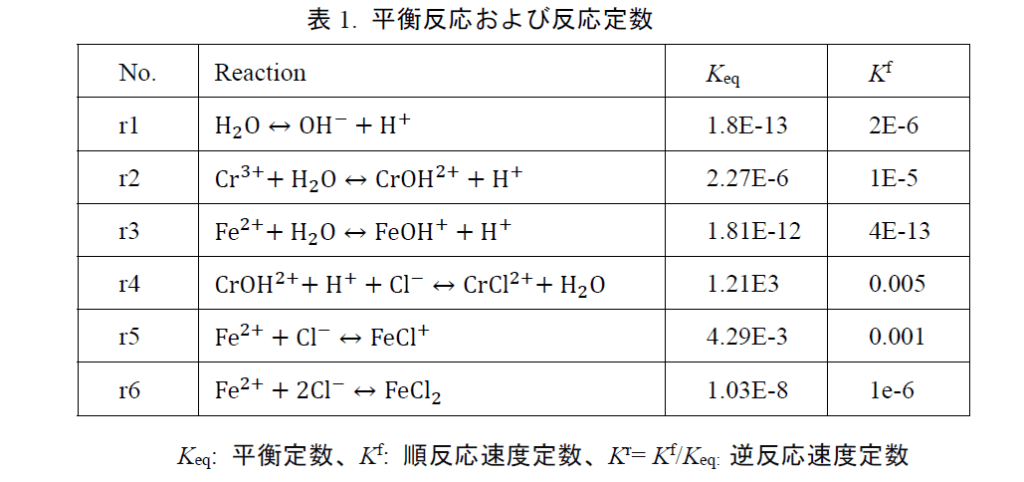
表1での平衡定数は，従来の $1 \mathrm{~L} ~(1 \mathrm{M}=1 \mathrm{~mol} / \mathrm{L}) ~$ に対する平衡定数から $1 \mathrm{~m}^{3}$ に換算した数値であ る。一義的には溶液内の化学反応は平衡定数により計算可能であるが，実際にすきま腐食が進行している場合は多種の金属イオンが溶出し，溶液の局所濃度が急激に変化するため，平衡状態に達していない条件となる²）。そこで本研究では溶液内の化学反応を可逆反応

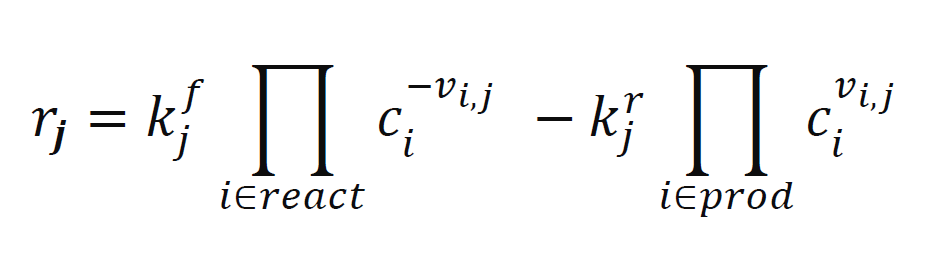
とする ${ }^{1)} . r_{j}$ は反応 $j$ に対する反応速度，$k_{j}^{f}, k_{j}^{r}$ はそれぞれ順反応速度定数と逆反応速度定数，$c_{j}$ は化学種 $i$ の濃度である。 $v_{i, j}$ は化学量論係数であり，reactとprocはそれぞれ反応物と生成物を意味する。

4）金属表面の電気化学反応は以下に表される。
$$
\begin{aligned}
& \mathrm{Fe} \rightarrow \mathrm{Fe}^{2+}+2 e^{-} \
\end{aligned}
$$

$$
\begin{aligned}
& \mathrm{Cr} \rightarrow \mathrm{Cr}^{3+}+3 e^{-} \
\end{aligned}
$$

$$
\begin{aligned}
& \mathrm{Ni} \rightarrow \mathrm{Ni}^{2+}+2 e^{-} \
\end{aligned}
$$

$$
\begin{aligned}
& \mathrm{O}{2}+2 \mathrm{H}{2} \mathrm{O}+4 e^{-} \rightarrow 4 \mathrm{OH}^{-}
\end{aligned}
$$

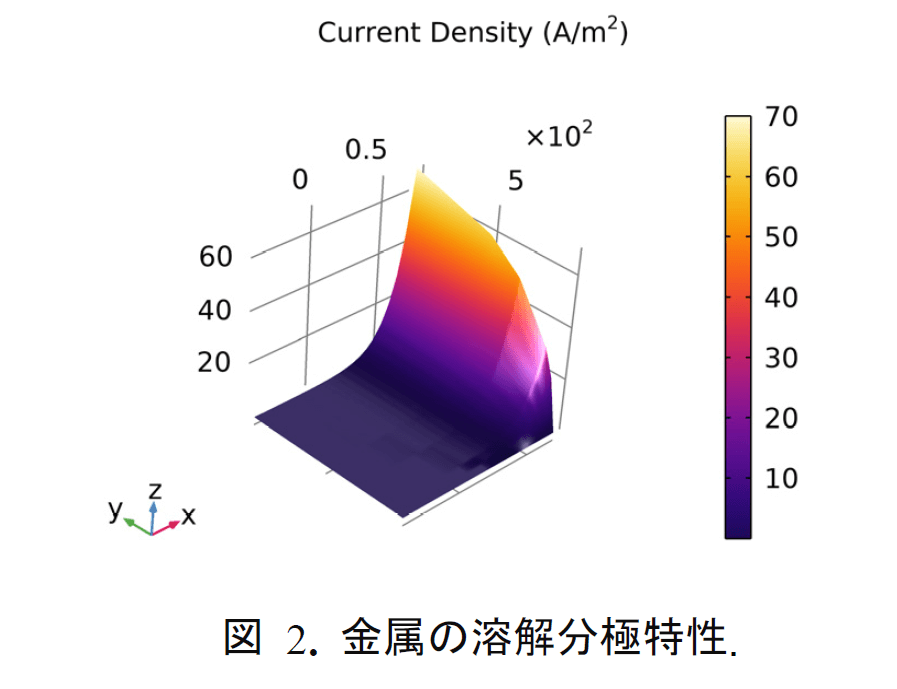
金属溶解の反応は図 2 に示した $\mathrm{Cl}^{-}$濃度に依存する分極特性 ${ }^{2)}$ を採用する。溶存酸素の還元反応はターフェル $i_{\mathrm{loc}}=-i_{0} \times 10^{\eta / A_{\mathrm{c}}}$ とする。ここで，$i_{0}$ は交換電流密度，$A_{\mathrm{c}}$ はターフェル勾配，$\eta$ は過電圧，$\eta=\phi_{s}-\phi_{l}-E_{\mathrm{eq}}$ である。 $\phi_{s}$ と $\phi_{l}$ はそれぞれ電極電位と電解質電位，$E_{\mathrm{eq}}$ は平衡反応で ある。酸素輸送の還元反応への影響はターフェル式での交換電流密度 $i_{0}$ に $i_{0}=i_{0, \mathrm{O}{2}} \times\left(c{\mathrm{O}{2}} /\right.$ $\left.c{\mathrm{O}{2}, \text { bulk }}\right)^{\alpha}$ とする．ここで，$i{0, \mathrm{O}{2}}$ は酸素輸送影響なしの交換電流密度，$c{\mathrm{O}{2}}$ と $c{\mathrm{O}_{2}, \text { bulk }}$ はそれぞれ金属表面および溶液中の酸素濃度である。 $\alpha$ は影響因子，ここでは，$\alpha=1.5$ である。

金属溶解の分極特性が 1 つだけあるため，溶解した金属原子Mを次の式で考慮する．
$$
\mathrm{M} \rightarrow \mathrm{M}^{n+}+n e^{-}
$$

溶解した金属イオンは，ステンレス成分の含有量により換算され，ここでFe ${ }^{2+}$ は $0.716, \mathrm{Cr}^{3+}$ は $0.197, \mathrm{Ni}^{2+}$ は 0.087 となり，$n$ は関与電子数， $2 \times 0.716+2 \times 0.087+3 \times 0.197=2.2$ である。

溶液内の拡散泳動と電流分布の計算方程式については例えば論文 ${ }^{2)}$ を参照されたい．

本書では解析モデルおよび解析結果を作成する手順を示す。
図 3 に $\delta=50 \mu \mathrm{~m}$ である 2 時間腐食した後の電解質電位， $\mathrm{Fe}^{2+}$ および $\mathrm{Cl}^{-}$の濃度分布を示ている。結果を明確的に示すため，すきま幅は 5 倍に拡大して表示された。

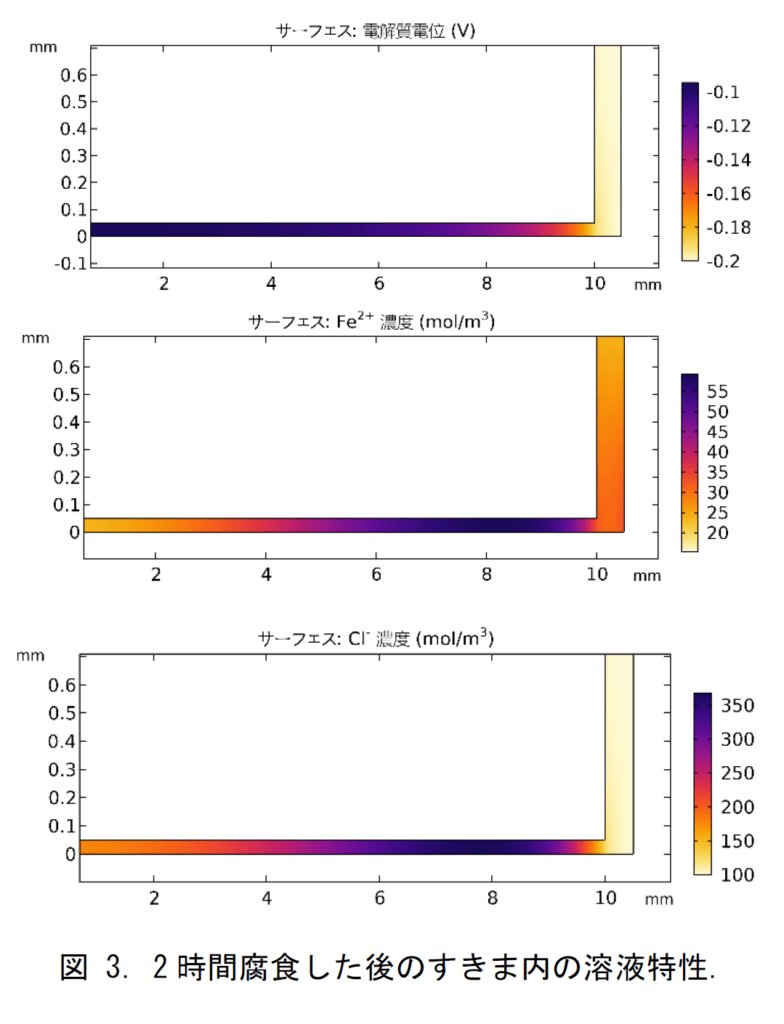
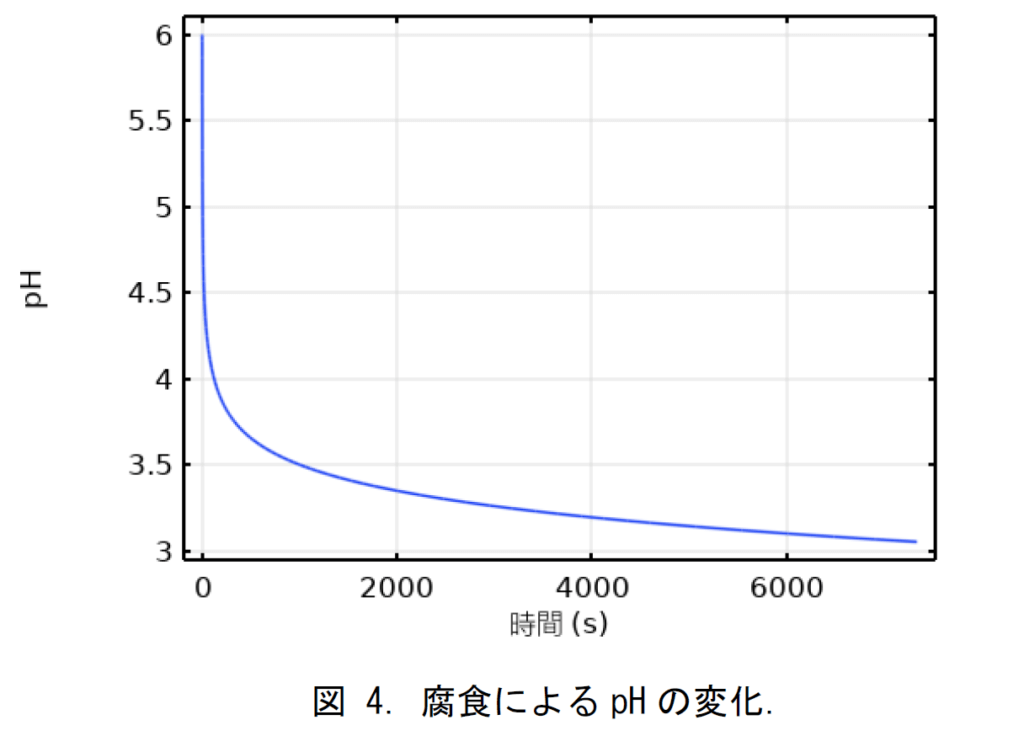
図 4 に示したように，すきまにおける pH はイオンの加水分解反応により，初期値の 6 から 3.2以下になった。従って，すきま内の腐食による溶液特性変化が検証された。

参考文献

1）Lizhu Tong and Masahiro Yamamoto，＂Change of Chemical Species with Progress of Crevice Corrosion＂，Proceedings of the 2020 COMSOL Conference，Boston（2020）．
2）佟立柱，永山達彦，汎用シミュレーションソフトによる腐食解析，計算工学，Vol．25，No．3， 4099－4104（2020）．

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。