フェーズフィールド法に基づくめっき解析におけるカソード表面形状変化のモデリング
めっきにおけるカソード表面形状は膜厚の変化によって変わることがある。形状変化の計算手法はめっきの数値解析モデルの構成要素の1つである。固定メッシュを用いて電極表面を間接的に表現する方法(界面捕捉法)と移動メッシュを用いて電極表面を直接的に表現する方法(界面追跡法)がある。代表的な形状変化の計算手法はEuler手法でのVOF(volume-of-fluid)法、レベルセット法、フェーズフィールド法およびLagrange法とEuler法が混合されたALE(arbitrary Lagrangian-Eulerian)法などが挙げられる。
フェーズフィールド法は、領域内にある境界の移動を、領域全体の相の状態を表すフェーズフィールド変数 ϕ の時間発展方程式を解くことで、境界を追従することなく表現できる手法である。時間発展方程式は、フェーズフィールド変数 ϕ を用いて、領域全体の自由エネルギーを定義した後、熱力学第 2 法則「系の自発的変化は自由エネルギーが時間とともに減少する方向へ進む」という原理に基づいて導出される。
レベルセット法におけるレベルセット関数を輸送する段階で距離関数としての性質が失われ、場合によっては界面が消失することがある。そのため、レベルセット関数の再初期化計算が必要になる。フェーズフィールド法は、この再初期化計算が不要であるため、計算安定性が向上する。
この計算例は、フェーズフィールド法を用いて、J. Deconinck1)の研究結果を定性的に再現する。フェーズフィールド法による計算結果はALE法による計算結果と比較することで計算効率を考察する。
本書では解析モデルおよび、図2の解析結果を作成する手順を示した。
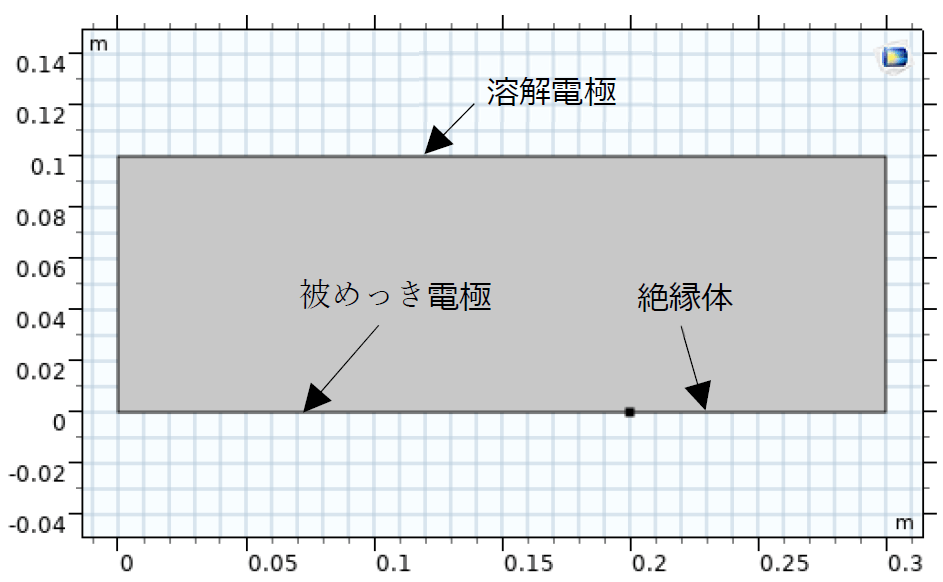
モデルは図1に示すような、2Dで作成され、溶解電極と被めっき電極の表面で構成される。計算ジオメトリは電解質領域のみがモデル化されている。電解質を、導電率0.23S/cmの0.8MH2SO4溶液であると想定する。\(Cu^{2+}\)の濃度勾配はモデルでは考慮していないため、2次電流分布を計算する。電極の材料は両方とも銅である。電極反応は以下のように考慮される。
\(Cu^{2+}(aq)\)+2\(esup^-\)⇔\(Cu(s)\)
電極反応速度モデルは、過電圧\(η\)と電極反応電流密度\(i_{loc}\)の間に比例関係が成り立つ
\(i_{loc}\)=\(η\)∙300(\(mA/(cm^2V\)))
被めっき電極(カソード)を接地し、溶解電極(アノード)に0.778Vの電位を設定する。カソードの法線方向から電極領域に向かうめっき速度\(v_{dep}\)は次式で算出される。
\(v_{dep}\) =-$\frac{i_loc}{2F}\frac{M}{ρ}$
ここで、\(F\)はファラデー定数、\(M\)はモル質量、\(ρ\)は密度である。
フェーズフィールド法によるめっき解析は以下の計算方程式を解く。
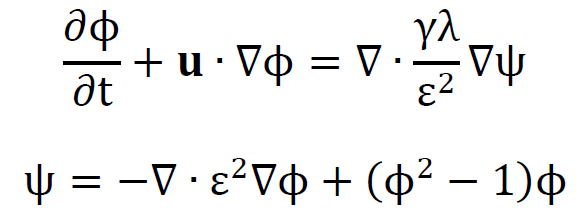
ここで、\(u\)は界面の移動速度, \(γ\)は易動度、\(λ\)は混合エネルギー密度、\(ε\)は界面の厚さである。フェーズフィールド関数\(ϕ\)は、次式で定義される。
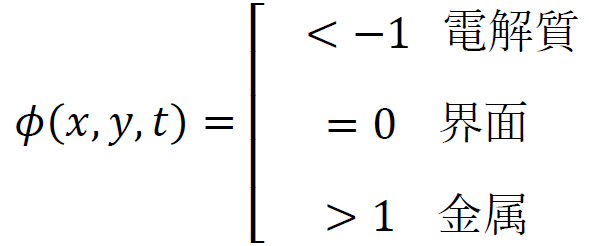
界面はϕ=0で表される。ここで、ε=${h}$max/16, ${h}$maxは要素サイズの最大値である。フェーズフィールド関数ϕを用いたデルタ関数は以下のように表される。
\(δ\)=$\frac{3}{4}$(1-ϕ2)|∇ϕ|
フェーズフィールド法によるめっき解析はカソード表面の皮膜領域を微小な電解質導電率がある電解質と定義し、次式で全領域の電解質導電率を求める。
\(σ\)=\(σ_{ed}\)×Vf2+\(σ_{el}\)×Vf1
ここで、\(σ_{el}\)と\(σ_{ed}\)はそれぞれ電解質・電極中の電解質導電率、Vf1とVf2はそれぞれ電解質・電極の体積比率を意味する。被めっき電極表面の化学反応は、以下のように電解質電流ソース\(Q_l\)で計算される。
\(Q_l\)=\(i_{loc}δ\)
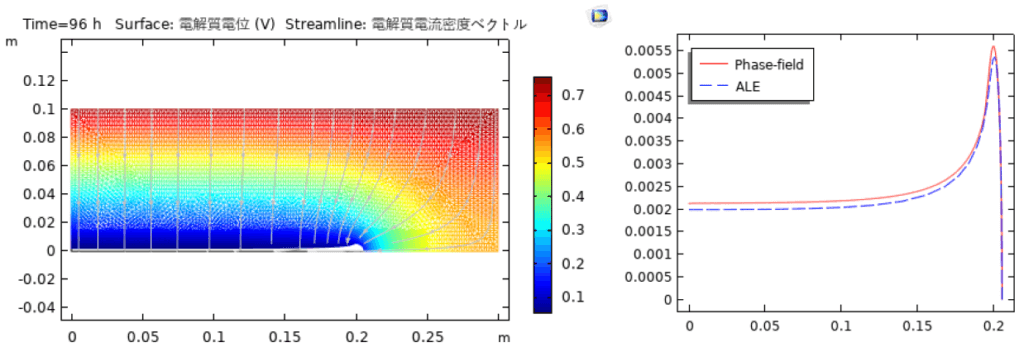
図2にめっきにより96時間後の電解質電位・電流密度、およびカソード表面形状を示している。固定メッシュに基づくフェーズフィールド法によりカソード表面形状の変化を捕捉することは可能になったが、カソード表面の近傍にはかなり細かいメッシュを作成する必要になることが示された。
参考文献
1)J. Deconinck, Mathematical modelling of electrode growth, J. Appl. Electrochem., Vol. 24, 212-218 (1994).
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。