めっきシミュレーションにおける移動メッシュ技術

予測・評価技術として活用可能なシミュレーション技術は、近年の製造業における開発において重要な役割を果たしている。めっきシミュレーションにおいてめっき液を攪拌するパドルの往復運動によってモデル形状を変化させることがある^1)-3)。形状変化の計算手法はめっきシミュレーションの構成要素の１つである。
本研究では、移動メッシュに基づくパドルの往復運動を表現する方法、ALE法（arbitrary Lagrangian-Eulerian、界面追跡法）によるめっき解析技術を示す. パドルめっきにおける流れの挙動のカソード表面の電流密度および膜厚分布への影響が表され、ALE法に基づく解析モデルを作成する手順を示した。

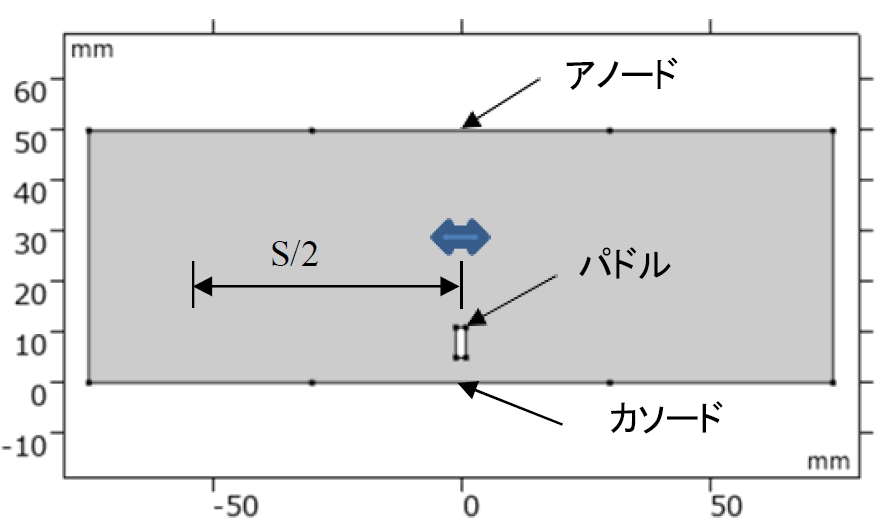
図1に示したパドルめっき槽⁴⁾においてパドルはカソード面の上の5mmに置き、往復運動ストローク(S)は 100mmである。パドルの幅と高さは2mmと6mmである。往復運動周波数は1Hzとする。アノードを接地し、カソードに 10 A/m²の平均電流密度を印加する。カソード表面の電極反応はCu²⁺(aq) + 2𝑒 → Cu(s)である。 電極反応速度モデルは、過電圧𝜂と電極反応電流密度𝑖_locの間の関係を

$$\eta =\dfrac{i_loc}{i_{o}}\dfrac{RT}{\left( \partial _{a}+\partial _{c}\right) }　　　　　　　　（1）$$

として表れる⁵⁾。ここで, Rは気体定数、Tは温度、Fはファラデー定数，(∂_a+∂_c)=2, i₀は交換電流密度、式(2)で表れる。

$$i_{0}= \left( \dfrac{c_{s}}{c_{b}}\right) ^{γ}i_{0} \left( c_{b}\right)　　　　　　　　（2）$$

ここで,𝑐_sはカソード表面の銅イオン濃度、c_bはめっき液中の銅イオン濃度、γは銅イオン濃度の電流密度への影響因子である。過電圧𝜂＝𝜙_ext-𝜙_o，𝜙_extは電極電位，𝜙_oは電極上のめっき液電位である。銅イオン濃度cの輸送および流れの挙動はNernst–Planck式および流体力学の基礎方程式により計算される。

パドル移動によるジオメトリの変形を変形ジオメトリを使用して計算を行う。
　・パドルのストローク(S)：100mm（移動幅 Sd=S/2:50mm）
　・パドルの往復運動周波数f：1Hz（周期T (1/f):1s）
　・パドルの位置をｘ：xd，ｙ：yd

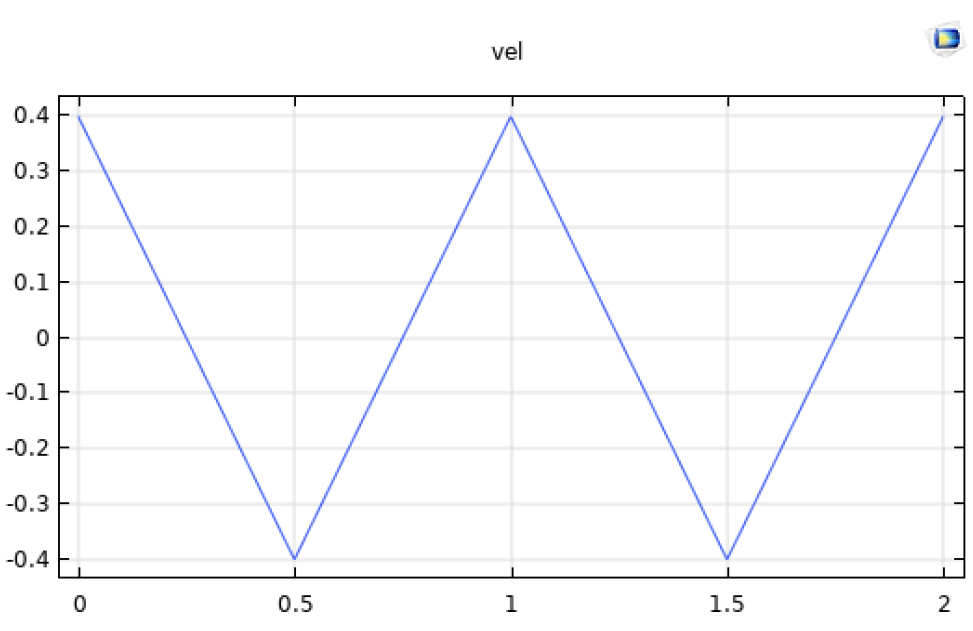
COMSOLでのメッシュの移動表現にCOMSOLの関数にてWaveform：波形を使用する。x軸のパドルの移動を波形関数名：vel,角振動数：2*pi/T，位相：pi/2，振幅：8*Sd/Tと設定する。移動速度はvel(mod(t,T)[1/s])[m/s]にて表し、時間毎の位置はintegrate(vel(s),s,0,mod(t,T))[m]で表す。

参考文献

1）D.E. Rice, D. Sundstrom, M.F. McEachern, L.A. Klumb, and J.B. Talbot, J. Electrochem. Soc., 135, 2777-2780 (1988).
2）D.T. Schwartz, B.G. Higgins, P. Stroeve, and D. Borowski, J. Electrochem. Soc., 134, 1639-1644 (1987).
3）G.J. Wilson and P.R. McHugh, J. Electrochem. Soc., 152, C356-C365 (2005).
4）岸本喜直,天谷賢治,早房敬祐,大西有希,“槽内電位の測定情報を利用した LSI ウェハ上のめっき電流密度の推定”, 日本機械学会第 22 回計算力学講演会, 2009.10.
5）L.Z. Tong, “Tertiary Current Distributions on the Wafer in a Plating Cell”, Proceedings of the 2012 COMSOL Conference in Boston. https://www.comsol.jp/paper/tertiary-current-distributions-on-the-wafer-in-a-plating-cell-13669.

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。