光パルスが照射するナノ薄膜の熱伝導、温度の時間発展モデル
技術が進歩しナノテクノロジーを駆使したデバイスが増えるにつれ、ナノスケールにおける熱輸送、特に物体と物体の継ぎ目である界面や薄膜材料における熱輸送が注目を浴びている。ナノスケールの薄膜は熱伝導に寄与するフォノンが界面で頻繁に散乱されるため、バルク材料と比較して熱伝導率が大きく低下することがあり、界面での熱輸送を無視できなくなる。
時間領域サーモリフレクタンス法(Time-Domain Thermoreflectance; TDTR)は非接触で測温が可能であり、高い時間分解能での物体温度の非定常測定を可能にした。ここでは、薄膜の面内熱伝導率測定に利用されるTDTR法を考慮する。この方法は、アルミニウムの反射率が温度に依存することを利用し、パルス加熱によって変化するプローブ光の強度を記録することで熱拡散現象を捉え、熱伝導率を得る光学的計測手法である。図1のように、測定したい薄膜をエアブリッジ化し、その中央にアルミ薄膜 (Aluminum)を用意し、アルミに集光した光パルスを照射する。

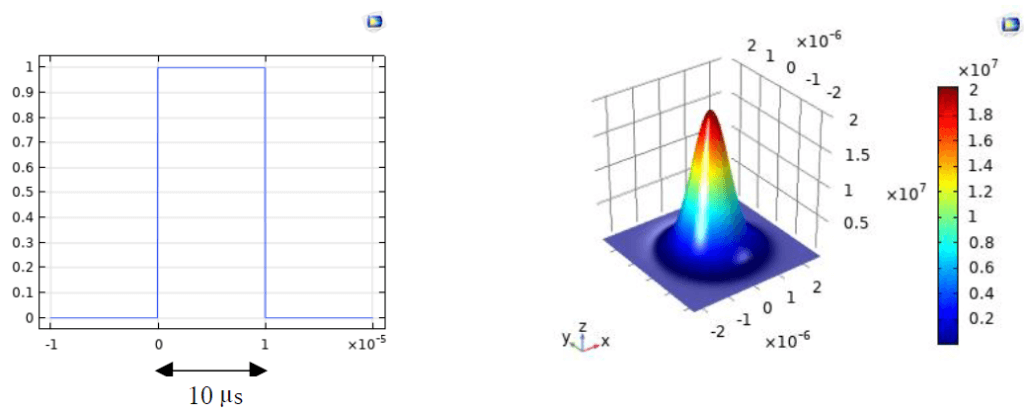
図2のような熱拡散時間よりも充分に短くなる光パルスを考慮する。10µsまで加熱し、その後は、Si薄膜を通じた熱散逸により温度が下がっていく。この減衰時間が熱拡散率の情報を含んでおり、密度と熱容量と合わせて、実験データを再現するような熱伝導率を本シミュレーションで探索し、得ることができる。
本書では、光パルスが照射するナノ薄膜の熱伝導、温度の時間発展を示すモデルおよび、2章以後に図3の解析結果を作成する手順を示した。
計算モデルは、光パルスを熱源とした伝熱計算である。ここでは、COMSOLの伝熱 (固体)インターフェースを利用する。支配方程式を式(1)に示す。
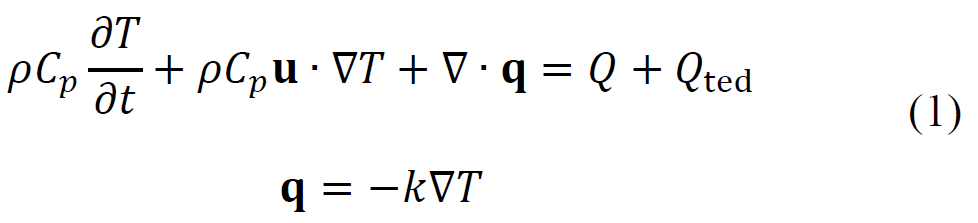
ここで、ρは密度、\(C_p\)は比熱容量、${T}$は温度、uは流速、qは熱流束、${k}$は熱伝導率、${Q}$は付加熱源、\(Q_{ted}\)は熱弾性減衰である。光パルスはアルミ薄膜においてqの境界条件として以下の式で定義される(1)。
$$I_{0}\exp \left( -\dfrac{x^{2}+y^{2}}{2\left( rg\right) ^{2}}\right) (2)$$
ここで、\(I_0\)はレーザーパワー、rgはガウス光線の波長である。
環境温度は295Kである。計算は熱源を印加する1µs前からスタートされ、熱源を印加している間は0.5µs間隔に出力時間を設定する。また、熱が逃げていく過程は減衰時間を得るために特に重要なため、過熱終了の直前からはより細かく、0.2µs間隔に設定する。COMSOLの時間ステッピングメソッドを「厳密」に設定することで、計算は指定された時間に従うが、必要に応じて、設定された時間の間に追加の計算も行う。
アルミ薄膜の中央に観測点を設定し、温度の時間発展を表示する。図3に観測点の位置と温度およびナノ薄膜の温度を示している。
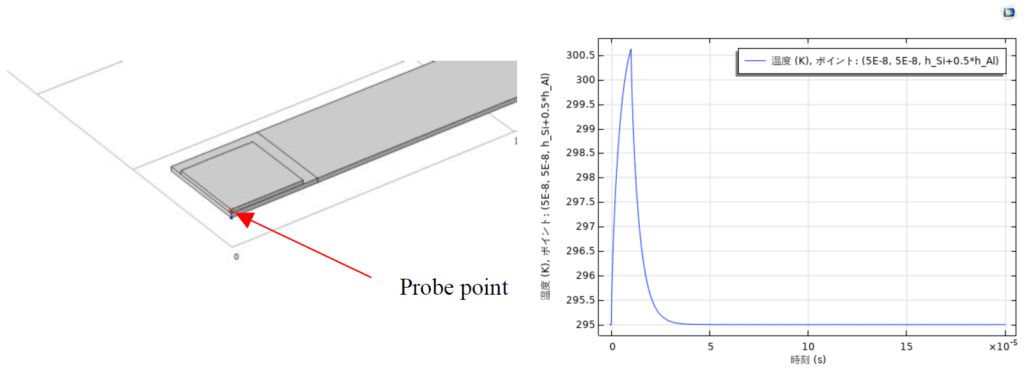
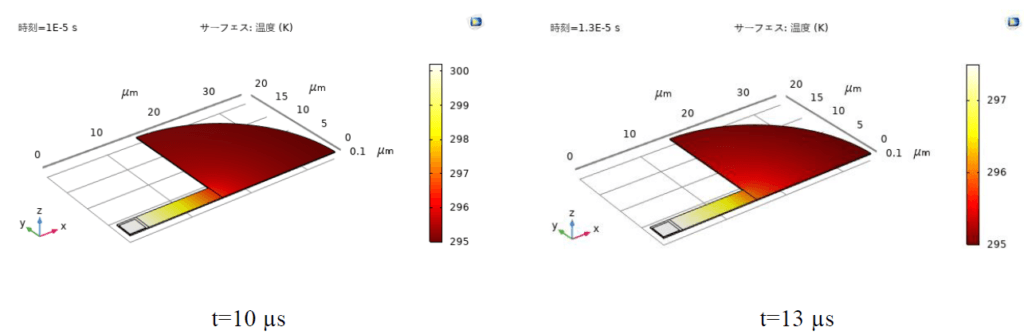
図3.温度の時間発展
図3(a)に示したように,観測点の温度は35µs以後に熱減衰が完了する。t=10µs,13µsの異なる減衰時間後のナノ薄膜の温度分布は図3(b)に示されている。
参考文献
1)R. Anufriev, A. Ramiere, J. Maire and M. Nomura, “Heat guiding and focusing using ballistic phonon transport in phononic nanostructures”, Nature Communications, DOI: 10.1038/ncomms15505.
*該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。