PDEモデルに基づく2D軸対称シミュレーション
軸対称問題は中心軸を含む任意の断面内で物理現象が同一となる問題である。この問題は二次元問題ときわめてよく似ており、円柱座標系を使う二次元的な解析手法が適用できる。COMSOL Multiphysicsは、軸対称物理インターフェースで円筒座標をサポートしている。しかしながら、COMSOL MultiphysicsのPDEモデルを利用する際、デカルト座標系から円筒座標系に手動で変更する必要がある。本チュートリアルでは、温度拘束された円筒の軸対称定常熱伝導解析を例として、COMSOL MultiphysicsのPDEモデルで座標変換する手法を紹介する。
軸対称定常熱伝導解析モデルを、図1に示す。
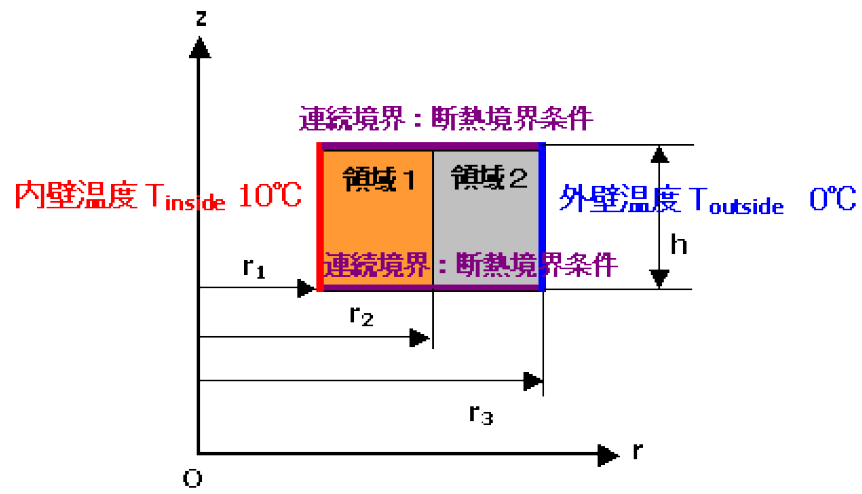
寸法と物性値は表1に示される。

ここで、κは熱伝導率である。境界条件では、内壁と外壁の温度はそれぞれ10℃と0℃で、上下の境界は断熱とする。このモデルに対して、半径方向 r[mm]の温度分布の解析解を次の式により計算できる。
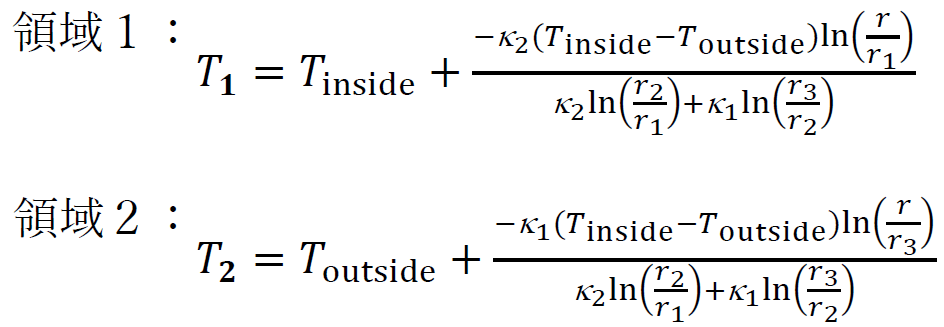
本書ではモデルおよび、図2の解析結果を作成する手順を示す。
定常熱伝導問題の微分方程式は次式で表される。
\(ρC_p u\)∙\(∇T+∇\)∙\(q=Q\)
${q}$=-${κ∇T}$
ここで、u=0とQ=0であり、計算方程式は以下のようになる。
${∇}$∙${(}$-${κ∇T)=0}$
ここで、${Γ}$=-${κ∇T}$は熱流束を意味する。COMSOLのPDEインターフェースは${∇}$∙${Γ}$を
$\frac{∂Γ_r}{∂r}$+$\frac{∂Γ_z}{∂z}$
で示す。これは${∇}$∙${Γ}$の円筒座標系の形式と一致しない。
円筒座標系では、${∇}$∙${Γ}$は
${∇}$∙${Γ}$=$\frac{1∂}{r}$$\frac{(rΓ_r)}{∂r}$+ $\frac{∂Γ_z}{∂z}$=$\frac{∂Γ_r}{∂r}$+$\frac{∂Γ_z}{∂z}$+ $\frac{Γ_r}{r}$
となる。COMSOLのPDEインターフェースはこの式の最後の項が含まれない。
COMSOLの物理インターフェースはデカルト座標系または曲線座標系に対応する微分演算子(共変微分. 物理法則は座標系に関わらず成り立つ)を利用するため、デカルト座標系から曲線座標系に変更する必要がなくなるが、PDE方程式ベースのモデリングでは、偏微分が使われるため、この座標系の変更が必要になる。本チュートリアルでは、COMSOLの係数形式PDEおよび一般形式PDEインターフェースを利用する。支配方程式は次式で表される。
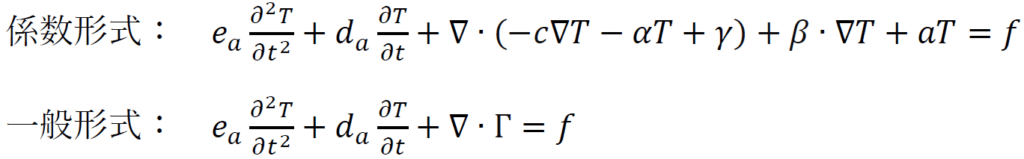
ここで、${∇}$=[$\frac{∂}{∂r}$,$\frac{∂}{∂z}$]、変数とその係数の扱いの詳細は例えば文献2)を参照されたい。${∇}$∙${Γ}$の発散式によって、係数形式PDEの係数は以下に定義できる。その以外の係数は0になる。

一般形式PDEの係数は${Γ}$に、-${κ×T_r}$と-${κ×T_z}$、${f}$に${κ×T_r/r}$で、以下のように設定される。

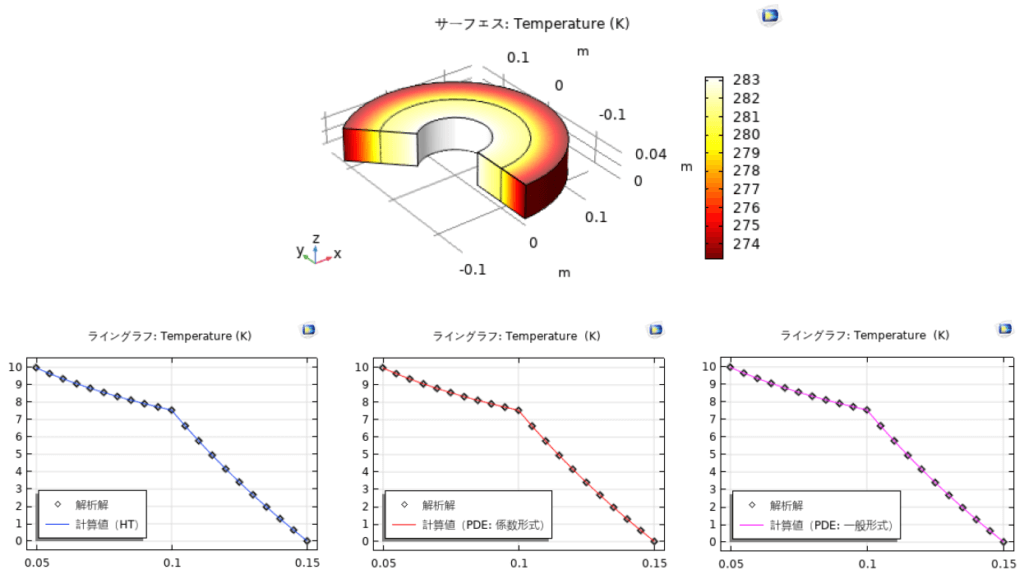
COMSOLの伝熱(固体)、係数形式PDEおよび一般形式PDEのインターフェースによって計算した結果を図2に示した。温度分布の計算結果は解析解とよく一致したことは示された。
参考文献
1)田中正隆,松本敏郎,中村正行,計算力学とCAEシリーズ: 境界要素法,培風館,1991.
2)COMSOL Multiphysics 5.6 – http://www.comsol.com/products and COMSOL Multiphysics Reference Manual.
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。