プラズマ窒化は古くから鉄鋼材料の表面改質用プロセスとして研究されてきた。パルスプラズマは、エッチング速度と堆積速度の向上、ダスト粒子の形成の減少、および堆積の均一性の特徴を示す。パルス放電窒化技術は、脆弱化合物層(窒化鉄化合物)の有無、窒化拡散層の深さを自在にコントロールし、理想の窒化層を形成できる。
近年、時間分解測定法による窒素とアルゴンにおけるパルスDC放電の電子密度分布の測定結果が掲載された1)。カソードに印加された電圧は-1~-2kV、パルス繰り返し周波数は0.4〜25kHz、デューティ比は10-50%である。この論文に対してDCパルス放電プラズマシミュレーションも既に報告された2)。
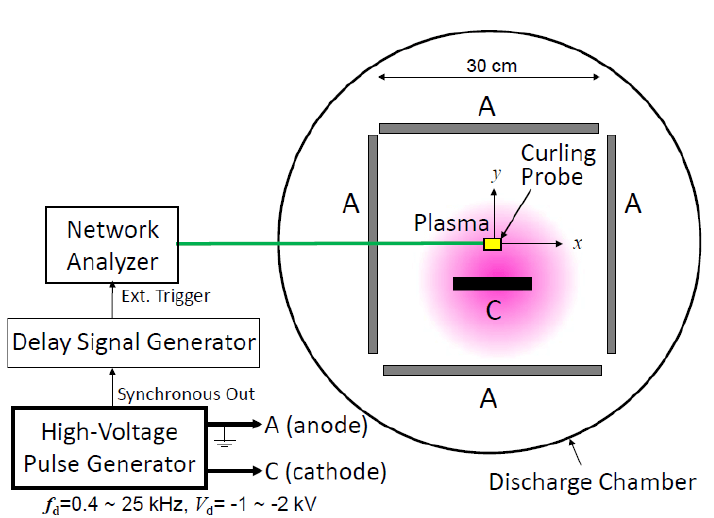
そこで本例題は報告された解析モデル2)を参考しモデルを再構築する.モデル構造図は図1に示され、モデル領域はアノードにより囲んでカソード以上の半分の領域とする.ガスは窒素、温度は300K、圧力は10Pa、パルス繰り返し周波数は1kHz、デューティ比は25%である。アノードは接地し、カソードは電圧が-2kVで印加され、外部RC回路と繋がる。バラスト抵抗は100Ω、プロッキング容量は50nFである。
本書ではモデルおよび、図3の解析結果を作成する手順を示した。
計算モデルは、電子、イオンと中性粒子の輸送、空間電荷場の計算方程式を連立して計算を行うが、紙数の都合でここではこれらの方程式の説明3)を省略する。電子輸送方程式におけるソース項には電子と分子や原子の衝突によって電子密度と電子エネルギーを変化することが含まれる。反応\(j\)の反応速度係数\(k_j\)は次の式で示される。
\(k_{j}=γ\int ^{\infty }_{0}εσ_j (ε)f(ε)dε,γ=(2q/m)\)
ここで、\(ε\)は電子エネルギー、\(σ_j(ε)\)は衝突断面積、\(f(ε)\)は電子エネルギー分布関数 (EEDF)、\(q\)は電子の電荷、\(m\)は電子の質量である。考慮した化学種および化学反応は表1と2に示される2)。
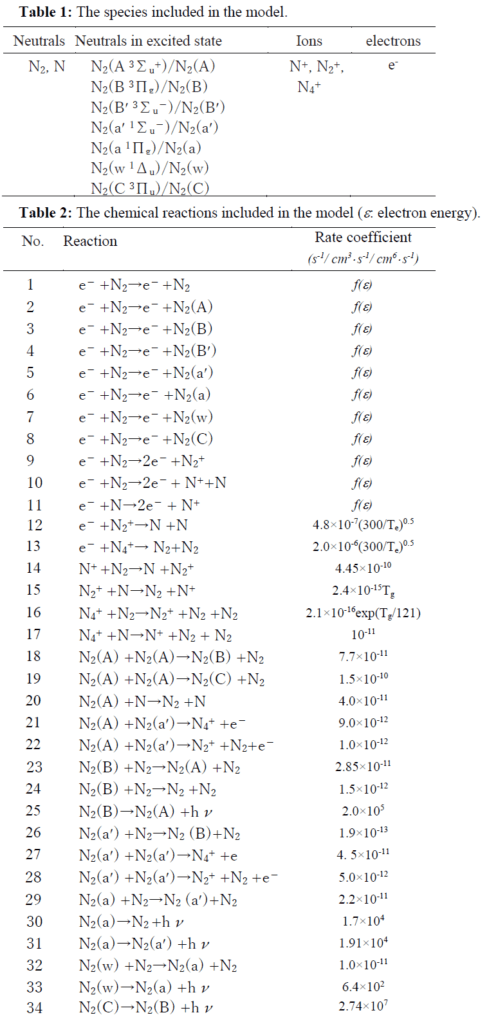
電子エネルギー分布関数はマックスウェル、カソードにイオン衝突による二次電子放出係数は0.25、二次電子平均エネルギーは2.5である。また、電極表面にイオンと励起種の付着係数は1, 窒素原子の付着係数は0.07である。
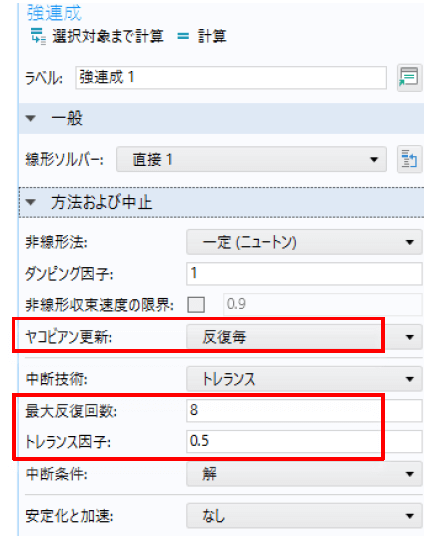
プラズマシミュレーションは、高度な非線形解析なので、ここではソルバーの追加設定する必要になっている。図2にCOMSOLの非線形時間依存ソルバーの強連成ソルバーの設定画面を示す。ヤコビアン更新は各タイムステップから「反復毎」に切り換えた。最大反復回数とトレランス因子も調整した。
図3にパルスDC放電シミュレーション結果を示している。計算時間は17時間42分でした。計算用のパソコンスペックは以下の通りである。
1.OS: WINDOWS 10
2.CPU: Intel(R) Xeon(R) CPU E5-1660 v2 @ 3.70GHz
3.メモリ RAM 128 GB
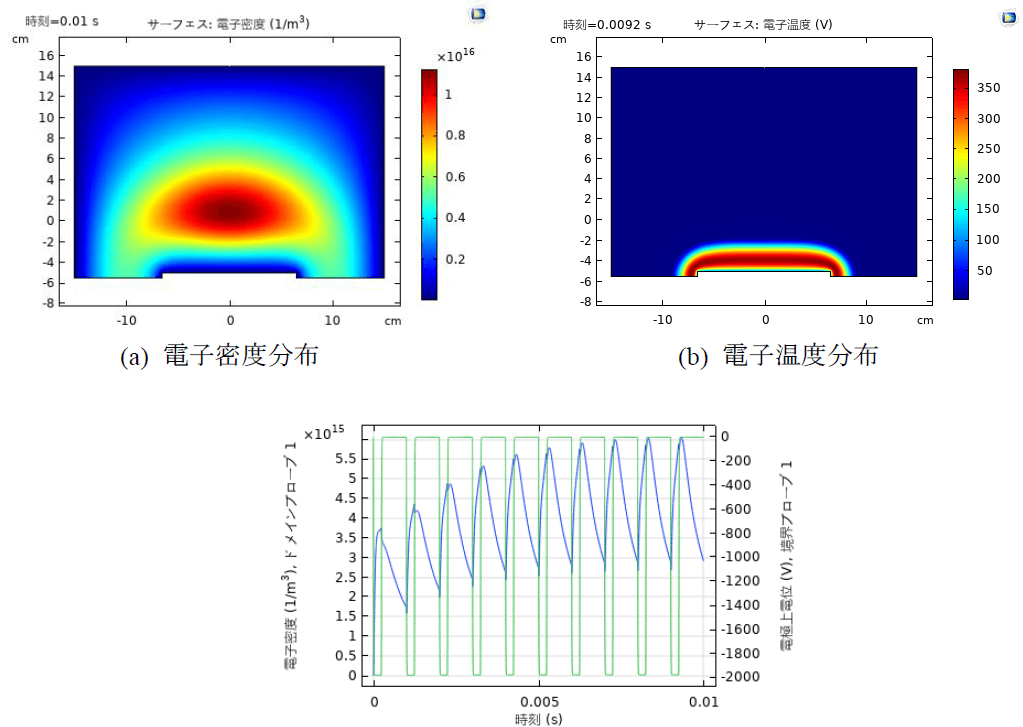
図3. パルスDC放電シミュレーション結果
参考文献
1)A. Pandey, W. Sakakibara, H. Matsuoka, K. Nakamura, and H. Sugai, “Time-resolved curling-probe
measurements of electron density in high frequency pulsed DC discharges”, Jpn. J. Appl. Phys., 55, 016101 (2016).
2)L. Z. Tong, “Simulation Study of High-Frequency Pulsed DC Discharges in Nitrogen”, Proceedings of the 2017 COMSOL Conference in Boston.
https://www.comsol.jp/paper/simulation-study-of-high-frequency-pulsed-dc-discharges-in-nitrogen-51903
3)放電・プラズマ気相シミュレーション技法調査専門委員会編,「放電・プラズマ気相シミュレーション技法:佟立柱,竹内希,3.3 COMSOL Multiphysicsを用いた非熱プラズマと熱プラズマの計算」,電気学会技術報告第1488号,pp. 70-74 (2020).
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。