ガスタングステンアーク溶接(GTAW)、別名,タングステンイナートガス溶接(TIG)は、船舶、パイプライン、自動車など広い領域に応用されている。このプロセスの数値シミュレーションは、溶接入力パラメーターに応じて溶接部の特性を予測する大きな挑戦に臨んでいるが、それは溶接を改善し、品質と生産性を向上させる(1)。このプロセスに関係する多くの物理現象の間の強い結合があるため、数値モデリングは複雑になる。
ステンレス鋼へのGTA溶接の数値解析では、熱伝達と流れの挙動に応じて、温度場、流れ場および電磁場は、統一されたMHDの定式化でモデリングできる。アークプラズマにおける電子、イオン、中性粒子の輸送は解かず、伝熱、流体、電磁気を解く。ここでは、ガスの絶縁破壊を示すことで、放電によるガスの導電率の変化およびガスの熱伝達を計算した。図1のように、解析モデルに以下の計算条件を考慮する。
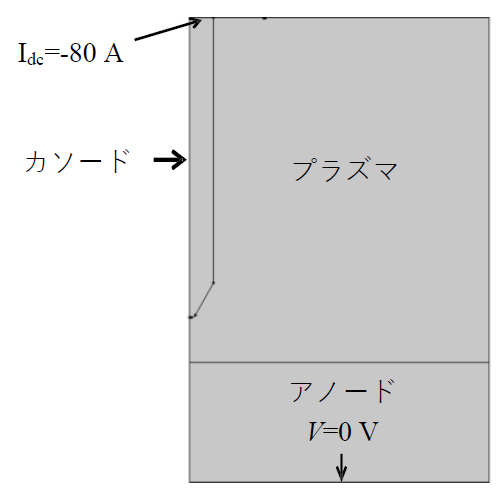
- 2D axial symmetry 2D軸対称
- Direct current (DC) at the cathode カソードでの直流
- Anode is grounded アノード接地
- Electrode polarity: Cathode 電極の極性:カソード
Direct current (DC) flows in one direction, resulting in a constant polarity
直流が一方向に流れるため、極性が一定である。
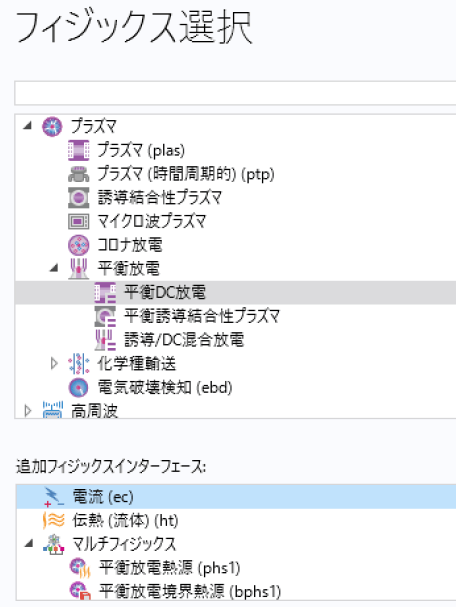
本書では、解析モデルおよび、2章以後に図4の解析結果を作成する手順を示す。計算用のCOMSOLインターフェースが図2に示している。プラズマ放電の熱源${Q}$を伝熱(流体)インターフェースに連成させて、支配方程式を式(1)に示す。
\(ρC_p\frac{∂T}{∂t}+ρC_pu\)∙\(∇T+∇\)∙\(q=Q\)
\(q\)=-\(k∇T\) (1)
ここで、\(ρ\)は密度、\(C_p\)は比熱容量、\(T\)は温度、\(u\)は流速、\(q\)は熱流束、\(k\)は熱伝導率である。熱源\(Q\)は、マルチフィジックス機能によって以下に定義される。
1)抵抗加熱 (オーム加熱):Q=J∙E
2)正味放射損失 \(Q_{rad}\)
3)エンタルピー輸送
$\frac{∂}{∂T}$($\frac{5k_BT}{2q}$)\((∇T\)∙\(J)\)
カソード境界熱源\(Q_b\)は式(2)で表される
\(-n\)∙(-\(k∇T\))=\(Q_b\)
\(Q_b\)=-\(|J_{elec}|ϕ_s\)+\(|J_{ion}|V_{ion}\) (2)
ここで、\(ϕ_s\)は表面仕事関数、\(V_{ion}\)はプラズマの電離電位、\(J_{elec}\)と\(J_{ion}\)はそれぞれ電子とイオンの電流密度である。
環境温度は20℃、ガスはアルゴンである。温度に依存するガスの導電率は図3に示されている。
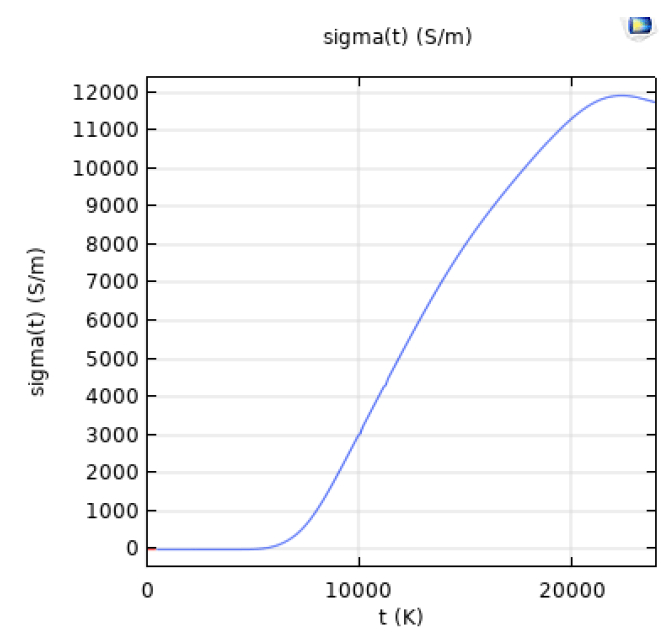
放電時間は1sとします。図4はガスの導電率及び温度の分布の計算結果である。ガスの絶縁破壊を生じる時の導電率及び温度の進展は示されている。
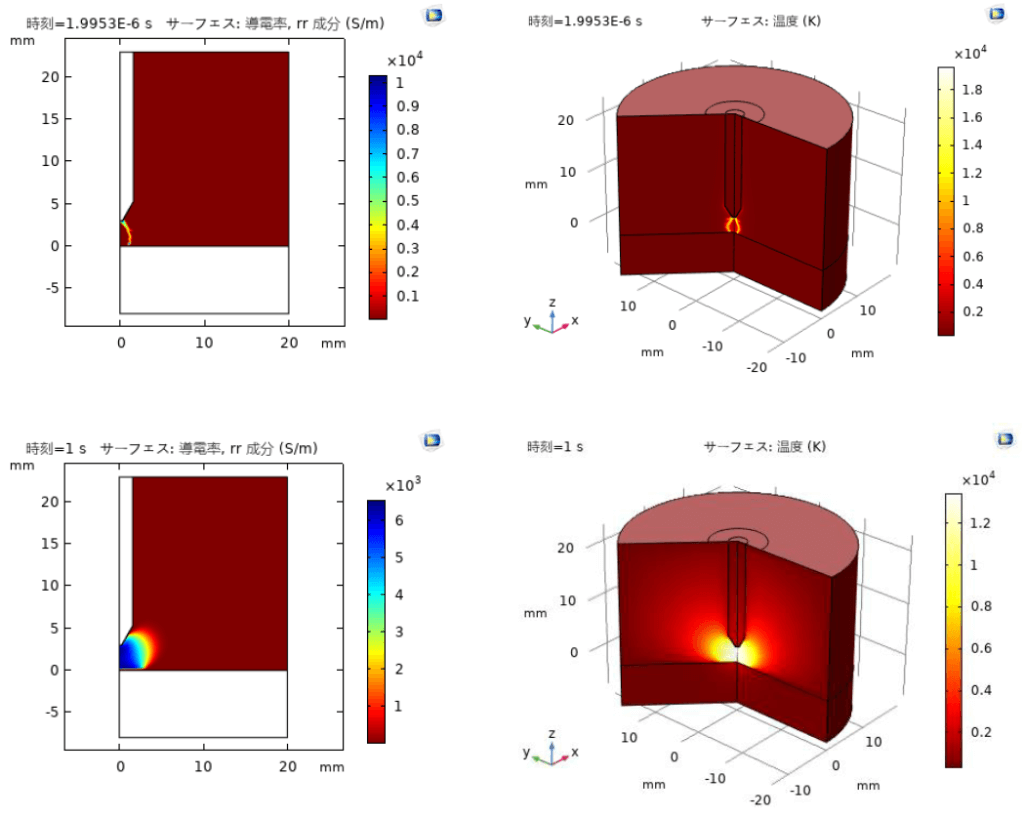
参考文献
1)A. Traidia, F. Roger, A. Chidley, J. Schroeder, T. Marlaud: “Effect of Helium-Argon Mixtures on the Heat Transfer and Fluid Flow in Gas Tungsten Arc Welding”, World Academy of Science, Engineering and Technology, 49, 2011.
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。