PDEモデルに基づくイオン風のシミュレーション
東京工業大学・竹内希先生ご提供

空気中でコロナ放電を形成すると、イオン風と呼ばれる気体の流れが発生する。本チュートリアルでは、COMSOL Multiphysics®のPDEモデルに基づいてイオン風の簡易的なシミュレーションモデルを紹介する。なお、同様の計算例が静電気学会誌の特集解説として掲載されているので、そちらも参考にしていただきたい。
イオン風のシミュレーションは、図1に示す軸対称二次元モデルで行った。計算領域は半径10mm、高さ10mmの円筒形状で、上部に設置した針電極の曲率半径はおよそ30μm，針電極先端と下部の平板電極のギャップ間距離は5mmである。平板電極を接地して針電極に負極性高電圧を印加すると、針電極先端で負極性コロナ放電が発生する。負極性コロナ放電の計算を厳密にシミュレーションする場合は、電離や付着といった電子衝突反応、分子の解離反応、生成された重粒子同士の反応、クラスターイオンの形成などを考慮する必要がある。また、負極性コロナ放電は、トリチェルパルスと呼ばれる不連続な形態となることもある。しかしながら、電子衝突反応の計算はメッシュサイズと時間刻みを極めて小さくする必要があり、メモリや計算時間が膨大となる。また、電離領域のイオン風に与える影響は小さく、ドリフト領域でのイオン分布が重要である。そこでこの簡易シミュレーションモデルでは、電子衝突反応の計算は行わずに、空気中での平均的な物性値を有する負イオンのみを荷電粒子として考慮し、針電極表面での負イオン密度を境界条件として与えることで、負極性コロナ放電のドリフト領域を模擬した。

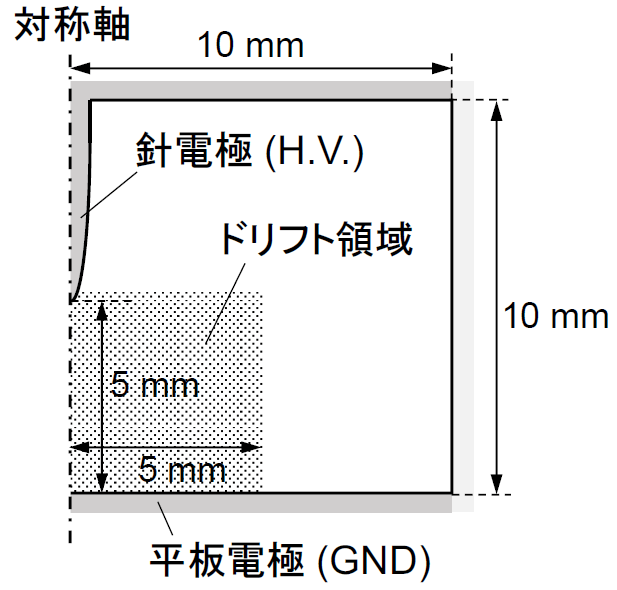
本書ではモデルおよび、図2の解析結果を作成する手順を示した。
計算モデルは、まず、ポアソン方程式と負イオンの連続の式の連成計算により、電位および負イオンの分布を計算した。計算コスト削減のため、およそ5×5mm²の領域を負イオンのドリフト領域とする。ポアソン方程式は下式で表される。

　　　　　-\(∇\)⋅\(ε_rε_0∇V\)=\(ρ\)

ここで、\(ε_0\)は真空の誘電率であり、比誘電率\(ε_r\)は1とした．また、空間の電荷密度\(ρ\)は、後述する負イオンの数密度\(N_n\)と電気素量\(e_0\)を用いて、

　　　　　\(ρ\)=-\(e_0N_n\)

と表される。針電極の電位を-5kVとして与えた。下部の境界（平板電極）の電位は零とし、また、上部と側面の境界では、電束密度の法線方向成分を零とした。
負イオンの連続の式を、係数型PDEモデルによって解く。

　　　　　$\frac{∂N_n}{∂t}$＋\(∇\)⋅(-\(D_n∇N_n\)-\(μ_nEN_n\))=0

ここで、\(D_n\)は空気中の負イオンの拡散定数、\(μ_n\)は負イオンの移動度、\(E\)は電界強度であり、

　　　　　\(E\)=-\(∇V\)

で表される。係数型PDEモデルにおける境界条件には、全ての境界でDirichlet条件を用いた。針電極表面での負イオン電荷密度を、対称軸からの半径方向距離rと時間tの関数としてr≤4×10^–5mの範囲で

　　　　　\(N_n\)=5×10¹⁷×(1-$\frac{r^4}{(4×10^-5)^4}$)×tanh⁡(10⁴t)

として与え、負イオンの初期数密度は宇宙線や放射線により形成された負イオンの数密度、～10⁶m^-3とした。
円筒座標系では、\(∇\)∙\(Γ\)は

　　　　　\(∇\)∙\(Γ\)=$\frac{1}{r}$$\frac{∂(rΓ_r)}{∂r}$＋$\frac{∂Γ_z}{∂z}$=$\frac{∂Γ_r}{∂r}$＋$\frac{∂Γ_z}{∂z}$＋$\frac{Γ_r}{r}$

となる。\(Γ\)=\(-D_n∇N_n\)-\(μ_nEN_n\)である。COMSOLのPDEインターフェースはこの式の最後の項が含まれない。次式で表す係数形式PDEの係数は表1に定義される。その以外の係数は0になる。

　　　　　\(e_a\)$\frac{∂^2 N_n}{∂t^2}$＋\(d_a\)$\frac{∂N_n}{∂t}$＋\(∇\)∙(-\(c∇N_n\)-\(αN_n\)＋\(γ\))＋\(β\)∙\(∇N_n\)＋\(aN_n\)=\(f\)

イオン風の駆動力は、荷電粒子に働くクーロン力となる。よって、負イオン分布の計算で得られた電荷密度\(ρ\)と電界強度\(E\)の積によりクーロン力\(F\)を求め、これをNavier–Stokes方程式の外力項に代入することで、イオン風の計算が可能である。
Navier–Stokes方程式は下式で表され、変数は流速\(U\)と圧力\(P\)であり、流体力学モデルで解く。

　　　　　\(ρ_g\frac{∂U}{∂t}\)＋\(ρ_g\)(\(U\)⋅\(∇\))\(U\)=-\(∇P\)＋\(μ_g∇^2U\)＋\(F\)

ここで、\(ρ_g\)は空気の密度、\(μ_g\)は空気の動粘性係数である。流体力学モデルにおける境界条件は、全ての境界ですべりなしとした。
計算領域における流速の初期値を零、圧力の初期値を1気圧とした。また、クーロン力を決定する電荷密度\(ρ\)と電界強度\(E\)には事前に計算した結果を用い、時間的に変化しないとして、流速および圧力の時間変化を計算した。
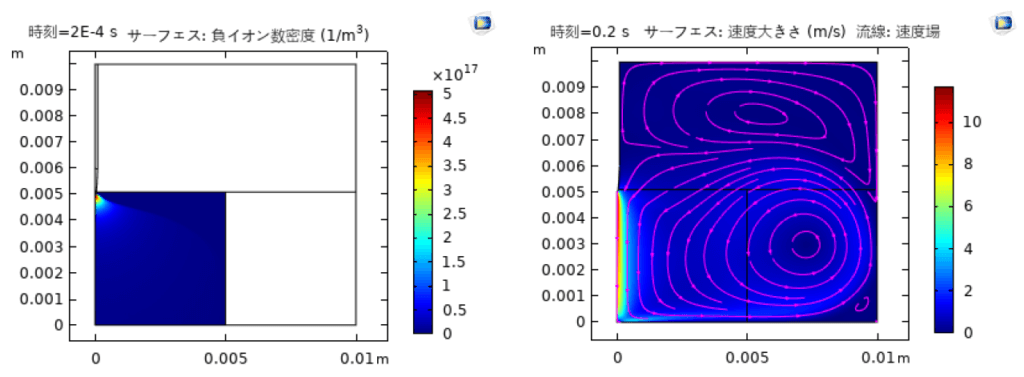
図2にコロナ放電によって発生した負イオン分布およびそれによるイオン風を示している。

参考文献

1）竹内希, “コロナ放電により発生するイオン風のCOMSOL Multiphysicsを用いたシミュレーション[特集解説]”, 静電気学会誌, Vol. 40, No. 4, pp. 168–171, 2016.
2）竹内希, “COMSOLおよびBOLSIGによるシミュレーションの実例”, 大気圧プラズマ工学ハンドブック, 第2編第2章, エヌ・ティー・エス, pp. 273–282, 2013.

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。