電気流体力学(EHD)解析
東京理科大学・元祐昌廣先生ご提供
マイクロ流体チップは、掌サイズの基板上に指紋サイズの極めて微細な流路を集積した器具で、少量の細胞・試薬での実験や分析時間の短縮が可能であり、化学・生物の実験効率化が期待されている。しかし、微小デバイス内部の流動は、高い比界面積があり、壁面との相互作用や電気的な力などの影響が強く、現象は複雑になる。ここでは、交流電場の印加によるマイクロ誘起流れ現象の解析を着目する。
図1にはタンパク質分析チップおよび解析モデル1)を示す。計算は静電場、温度場および流動場を連成している。各モデルは図2に示されている。ここでは、AC信号のRMS値を利用し、同じ熱効果を生み出すのであると考えられる。
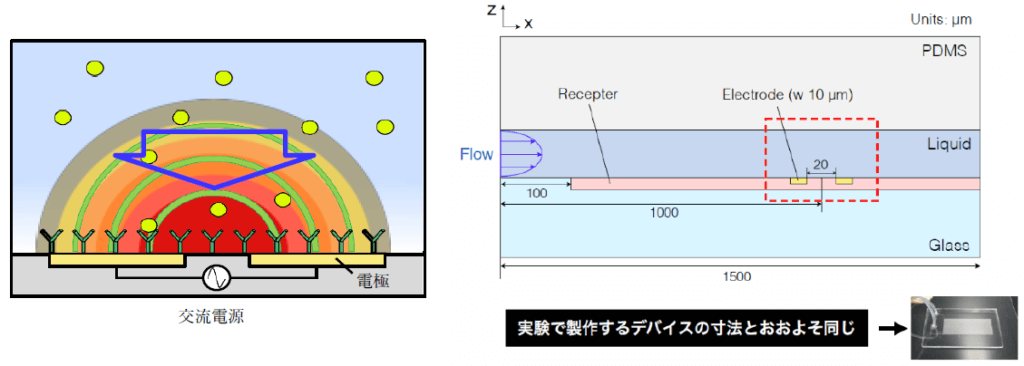
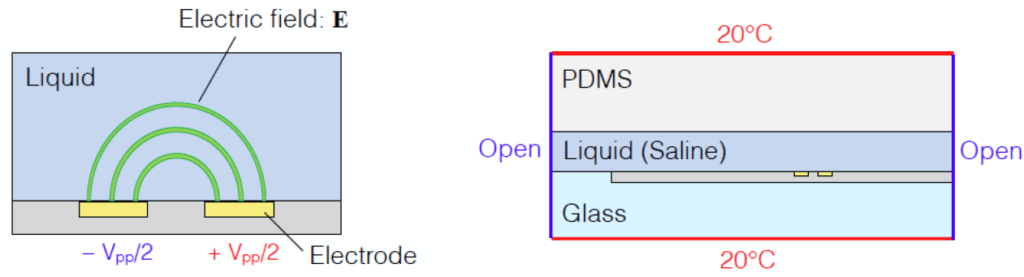
本書では、静電場、伝熱およびクリープ流(ほふく流)を連成する電場誘起流れ現象を示すモデルおよび、2章以後に図4と図5の解析結果を得る手順を示す。
計算モデルは、以下に示した計算手順
交流電場=>温度上昇(ジュール加熱)=>流れ物性勾配=>電磁力が作用=>誘起流れの発生
を考慮する。
AC信号のRMS値を利用する静電場の支配方程式は次式で表される。
\({\bf E}\)=-\(∇\)\(V\)
ここで、は比誘導率である。ジュール熱源は
\(Q\)=$\frac{1}{2}$σ|\({\bf E}\)|2
この熱源を、COMSOLの伝熱 (流体)インターフェースに導入する。
\(ρC_p\frac{∂T}{∂t}\)+\(∇\)∙\({\bf q}\)=\(Q\)+\(q_0\)
\({\bf q}\)=-\(k∇T\)
ここで、\(ρ\)は密度、\(C_p\)は比熱容量、\(T\)は温度、 \(k\)は熱伝導率、\(Q\)は熱源、\(q_0\)は面外熱流束である。流体の物性は図3に示した温度に依存するデータであると考えられる。
環境温度は20℃である。静電場と伝熱を連成計算して、流れ計算を行う。クリープ流れインターフェース(spf)を利用する。支配方程式は次式で表される。
0=\(∇\)∙[-\(p\)\({\bf I}\)+\(u\)+(\(∇\)\({\bf u}\)+(\(∇\)\({\bf u}\))\(T\))+\({\bf F}\)
\(ρ∇\)∙\({\bf u}\)=0
ここで、\({\bf u}\)は速度、\(p\)は圧力、\(μ\)は粘性係数、\({\bf F}\)は電磁力である。COMSOLには\({\bf F}\)が体積力で設定される。COMSOL変数に次式2)で計算される。
\({\bf F}\)=-$\frac{1}{2}$[($\frac{∇σ}{σ}$-$\frac{∇ϵ}{ϵ}$)∙\({\bf E}\)$\frac{ϵ\bf E}{1+\left( ωτ\right) ^{2}}$]+$\frac{1}{2}$ |\({\bf E}\)|2\(∇ϵ\)
ここで、\(τ\)=\(ϵ/σ\)は緩和時間である。
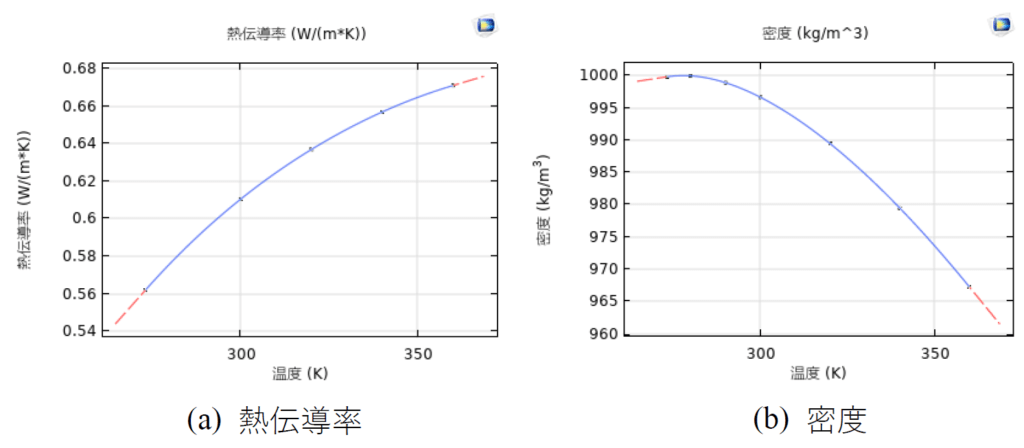
液体試料の熱伝導率と密度などの物性を補間関数として設定して、以下の定常計算を行う。
ステップ1:定常 静電場(es)と伝熱(流体)(ht)
ステップ2:定常 クリープ流 (ht)
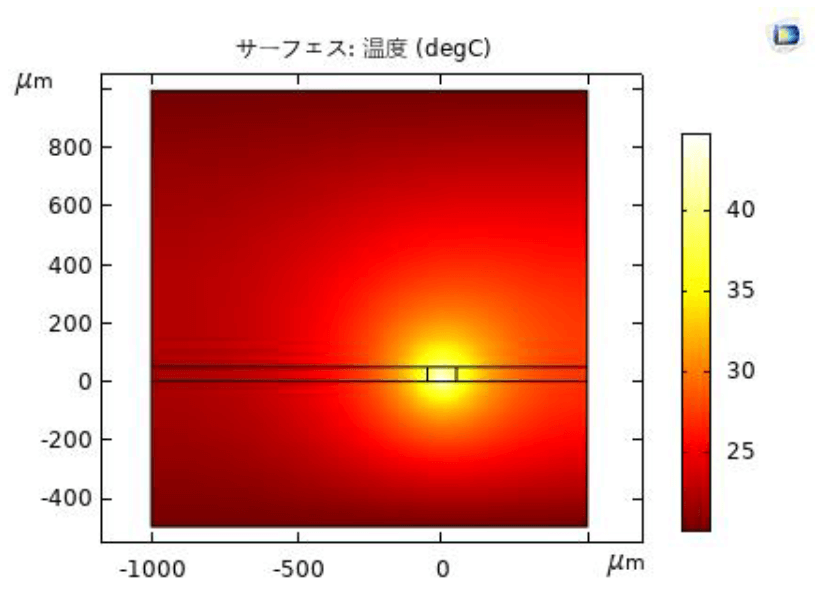
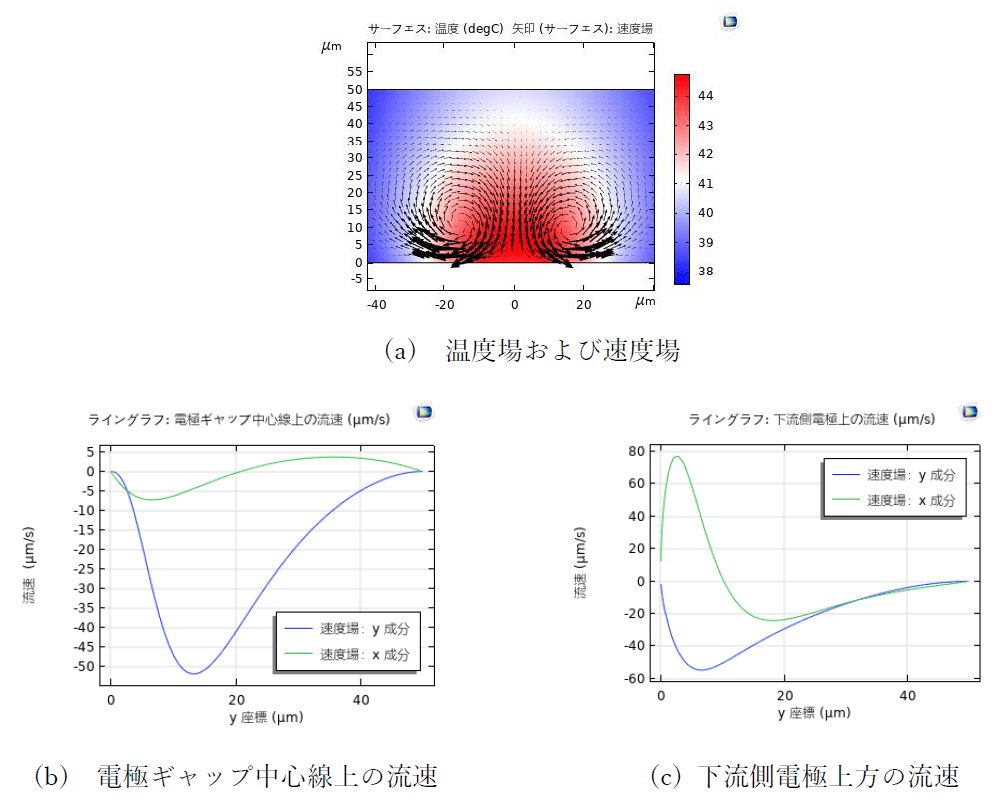
図4に全体の温度分布を示している.誘起流れ場は、図5に示される。図5(a)は温度場および速度場である.図5(b)と図5(c)は電極ギャップ中心線上の流速分布および下流側電極上方の流速分布である。
参考文献
1)元祐昌廣、数値シミュレーションと実験を駆使した最先端熱流体システム開発、COMSOL Conference 2018 Tokyo.
2)A. Ramos, H. Morgan, N. G. Green and A. Castellanos, “Ac electrokinetics: a review of forces in microelectrode structures”, J. Phys. D: Appl. Phys. 31 (1998) 2338–2353.
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。