回転電極による電解セルの電流分布解析 ~3次電流分布シミュレーション計算例 ~
回転電極は腐食測定、2次電池、燃料電池の研究、微量分析、ボルタンメトリー、めっき添加剤の分析 (CVS)種々のアプリケーションがある。
円筒形の絶縁体の底面に埋め込まれたディスク円盤型の電極が溶液と接触するように構成され、電極の中心を通る軸のまわりで回転する電極である回転電極は電極表面に強制的対流を生成し、電極/電解質インターフェースに熱のおよび濃度の大きな変化を防止できるため静止電極を用いる場合と異なり、一定回転速度において、定常電流電位曲線を得ることができる。
従って、回転電極は めっきや腐食における電極分極特性の測定によく利用されている。
図1には電解セルにおける回転電極の電流分布解析モデルを示す。電解質は\(0.3MCuSO_4\)と\(1.9MH_2SO_4\)で構成される酸性硫酸銅溶液である。直径6mmの回転ディスクを考慮する。直径3mmの作用電極が回転ディスクの下部中央に配置されている。
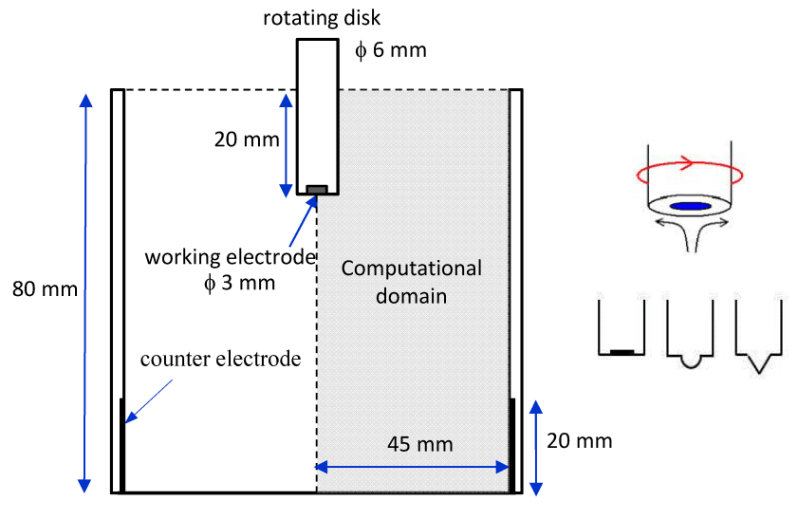
本書では、流れ(層流)と電流分布の計算を連成するモデルおよび、2章以後に図2と図3の解析結果を得る手順を示す。
流体の慣性力と粘性力の比で表されるレイノルズ数を次の式で計算できる。
\(R_e\)=\({ρωr_d}^2/μ\)
ここで、\(ρ\)は密度、\(μ\)は粘性係数、\(ω\)は回転速度、\(r_d\)は回転ディスクの半径である。
図1に示す回転ディスクは\(r_d\)=3mmであり、動粘度は\(ν\)(=\(μ/ρ\))= 1×10-6m2/sであるため、\(ω\)=2000rpm(つまり、209rad/s)の回転速度に対するレイノルズ数はRe=1881である。
層流から乱流への移行の臨界レイノルズ数は、回転ディスク(RDE)に対して105になるため、本モデルは層流の計算を行う。
計算は、COMSOLの層流と3次電流分布インターフェースを用いて行われた。計算用のパラメーターは表1に示す。

アノードは接地として、カソード表面に分極特性および平均電流密度を与える。カソード表面の分極特性は以下のターフェル式で示される。
\(i\)=\(-i_0exp10(-\frac{η}{b_c})\frac{c_w}{c_b}\)
ここで、\(i_0\)は交換電流密度、\(b_c\)はターフェル勾配、\(c_w\)はカソード表面濃度、\(c_b\)はバルク濃度である。過電圧は\(η\)=\(Φ_s- Φ_l-{E_e}_q\)であり、\(Φ_s\)は電極電位、\(Φ_l\)は電解質電位、\({E_e}_q\)は平衡電位である。
本モデルは、流れから電流分布までの弱連成計算を考慮し、以下の定常計算を行う。
ステップ1:定常層流(spf)
ステップ2:定常3次電流分布 (ネルンスト・プランク) (tcd)
図2は回転ディスクによる電解セル内の流速分布である。回転速度は300 rpmであり、回転ディスクの近傍に流れが加速されることが示された。
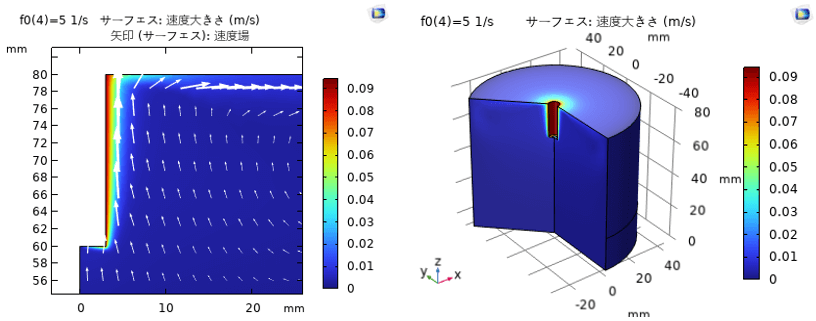
図3(a)は回転速度300rpmの時の電解質電位および電解質電流密度の計算結果である。回転数による作用電極の近傍のイオン濃度変化および作用電極表面の電流密度分布はそれぞれ図3(b)と図3(c)に示された。

参考文献
1)L.Z. Tong, “Simulation Study of Tertiary Current Distributions on Rotating Electrodes”, Transactions of the Institute of Metal Finishing, 90 (3), 120-124 (2012).
2)D.R. Gabe, “Rotating electrodes for use in electrodeposition process control”, Plating & Surface Finishing 82, 69-76(1995)
*該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。