近年、二次電池に比べて電気化学キャパシタが高出力、長寿命の蓄電デバイスとして注目を浴び、盛んに研究開発が行われている1)。その中でも電気化学キャパシタの代表である電気二重層キャパシタ(EDLC) は高い信頼性、低環境負荷、入出力特性の高さなどの特徴を持ち、様々なアプリケーションに適用されている。図1に示すように電気二重層キャパシタ2)は電極表面と電解液との界面に生じる電気二重層を利用し、電荷を蓄える蓄電デバイスである。充放電時に正極表面にマイナスイオンが、負極表面にプラスイオンが物理的に吸脱着する。その際に電極と電解液との間に化学反応を伴わないため、充放電速度が速く、かつ繰り返し充放電による劣化が少なく長寿命である。
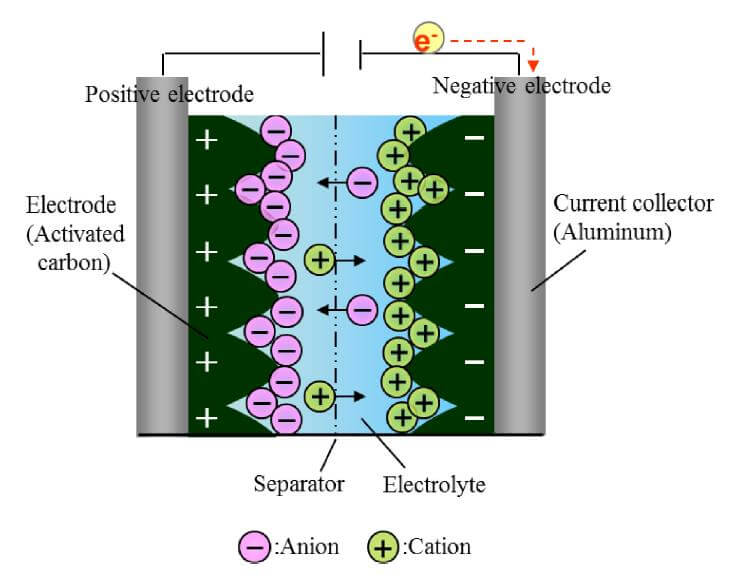
電気二重層キャパシタにおける幅が数ミクロンの多孔性炭素電極はナノメートルの細孔径である凝集体である。多孔性 電極理論は電気化学モデルとしてリチウムイオン二次電池の解析に非常に多く応用されてきた3)。多孔性電極理論とともに希釈溶液理論は電気二重層キャパシタの解析に応用されている4)。
多孔性電極のマトリックスと電解液における電流密度は以下のように1Dで表現される4)。
\(i_1=-σ\frac{∂Φ_1}{∂_x}\)
\(i_2=-κ\frac{∂Φ_2}{∂x}-κ\frac{RT}{F}(t_+-t_-)\frac{∂lnc}{∂x}\)
ここで、\(Φ_1\)と\(Φ_2\)はそれぞれ電極(マトリックス)電位と電解質電位、\(σ\)と\(κ\)はそれぞれ電極(マトリックス)と電解質の導電率、\(c\)はバイナリ電解質の塩濃度、\(t_+\)と\(t_−\)はイオンの輸率である。
\(t_+=\frac{D_+}{D_++D_-}~,~t_-=\frac{D_-}{ D_++D_- }~,~t_++t_-=1\)
電解液における電荷保存および物質収支は次式となる。
\(\frac{∂i_2}{∂x}=aC\frac{∂(Φ_1-Φ_2)}{∂t}\)
\(𝜀_2\frac{∂c}{∂t}=D\frac{∂^2c}{∂x^2}-\frac{aC}{F}(t_-\frac{dq_+}{dq}+t_+\frac{dq_-}{dq})\frac{∂(Φ_1-Φ_2)}{∂t}\)
ここで、\(ε_2\)は多孔性電極における電解質の体積比率、\(aC\)はキャパシタンス、\(\frac{dq_+}{dq}\)と\(\frac{dq_-}{dq}\)は電気二重層キャパシタの電極表面の化学種濃度の変化に対する表面電荷の変化、次式で反映される。
\(z_jFj_j=-C\frac{dq_j}{dq}\frac{∂(Φ_1-Φ_2)}{∂t}\)
ここで、下付き文字\(j\)は 化学種を意味する\(\frac{dq_+}{dq}=\frac{dq_-}{dq}=−0.5\)である4)。
本書では解析モデルおよび図2の解析結果を作成する手順を示す。
多孔性電極の有効導電率および電解質の有効拡散係数は以下のように定義される。
\(σ^{eff}=\frac{ε_1}{τ_1}σ~,~D^{eff}=\frac{ε_2}{τ_2}D,\)
ここで、\(ε_1\)は多孔性電極のマトリックスの体積比率、\(τ_1\)と\(τ_2\)は多孔性電極のマトリックスと電解液のねじれ率である。電気泳動、イオン速度\(u_j\)はネルンスト・アインシュタイン方程式で表される。
\(u_j=\frac{D_j}{RT},\)
計算ジオメトリは、0.93Mの塩濃度である活性炭-セパレーター-活性炭の1Dモデルである。図1に示すような、活性炭が電極材料として用いられる。Verbruggeら4)の試験方法
まず、電気二重層キャパシタは0Vまで放電し、その電圧で300秒間保持する。その後、1.7Vのプリセット電位に100Aの定電流で充電される。次に、一定の1.4Vが5 秒間印加され、その後、電気二重層キャパシタが開回路電圧で180秒間緩和する。この 操作を繰り返して、プリセット電位は0.1V刻みで1.8Vから2.4Vまで電気二重層キャパシタを充放電する。
に基づいて電気二重層キャパシタの充放電の計算を行い、試験値と比較する。
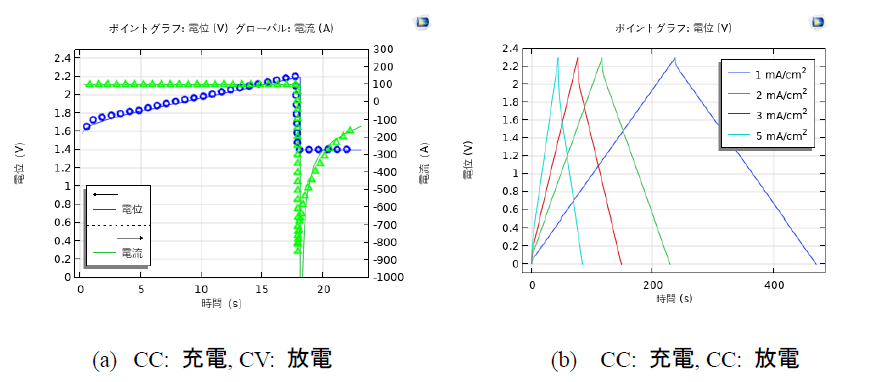
図2は電気二重層キャパシタの充放電の計算結果である。計算値は試験値(記号)4)と一致したことで、希釈溶液および多孔性電極の計算理論が電気二重層キャパシタの解析に適することを明らかにさせた。
参考文献
1) 野原愼士, 電気化学キャパシタの基本原理と特徴, 表面と真空 62 (12), 2019: 698–702.
2) 古賀淳史, 電気二重層キャパシタの技術動向, 表面と真空 62 (12), 2019: 717–717.
3) 佟立柱,福川真,リチウムイオン電池・全固体電池のシミュレーション技術-Liイオンの輸送と反応に基づく電気化学モデルから集中パラメータによる電池モデルまで-計算工学 , Vol. 25, No. 4, 2020: 4145-4150.
4) M.W. Verbrugge and P. Liu, Microstructural Analysis and Mathematical Modeling of Electric Double-Layer Supercapacitors, J. Electrochem. Soc. 152 (5), 2005: D79–D87.
*該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。