ステンレス鋼は耐食性に優れ、また優れた金属光沢を維持できるため、多くのところで使用さ れている。特に SUS304 (18Cr-8Ni)ステンレス鋼は流し台や水回りの材料として住宅用、また、化学プラントや建築材料など数多くのところで使用されている。しかしながら、塩化物イオン $\left(\mathrm{Cl}^{-}\right)$が存在する環境では孔食が発生することが知られている。SUS304 鋼の孔食については、古 くよりその発生と成長過程が研究され、解説にもまとめられている ${ }^{1,2)}$。彼らの記載内容をまと めると、SUS304 鋼は通常は表面が不働態化しているので、腐食速度は非常に小さいが、塩化物 イオン濃度の高い環境では、不働態皮膜の一部が破壊されそこから金属の溶解が起きる。その時 に金属の電位が貴な状態にあることが進展の条件で、孔食は比較的きれいな楕円球状になる。こ の場合に、電位が高い方が楕円球状になり易く、低い電位では再不働態化もしくは孔食内の一部 のみが腐食し続ける形態になる。また、孔食の進行過程で孔食内の溶液組成の影響で、孔食が進行し続けるか、止まるかを決めている。
孔食部の溶解速度は非常に大きく、$300 \mathrm{sec}$ で $50 \mu \mathrm{m}$ の深さにまで成長することもある ${ }^{3)}$。孔食部の電流密度を直接測定することは難しいが、孔食をモデル化した電極を用いて測定すること で推定されている ${ }^{4,5)}$。本モデルでは、孔食の成長過程を変形ジオメトリー計算で再現すること を行った。さらにその状態で、ステンレス鋼の局部腐食時の $\mathrm{pH}$ 低下の原因と考えられている $\mathrm{Cr}^{3+}$ イオン加水分解反応 $(1)$ )連成して計算した。また、$\mathrm{H}_{2} \mathrm{O}$ の解離反応 $(2)$ も考慮した。

$$
\mathrm{Cr}^{3+}+3 \mathrm{H}_{2} \mathrm{O} \rightarrow \mathrm{Cr}(\mathrm{OH})_{3}+3 \mathrm{H}^{+} \tag{1}
$$

$$
\mathrm{H}_{2} \mathrm{O} \rightarrow \mathrm{OH}^{-}+\mathrm{H}^{+} \tag{2}
$$

式(1)の反応の平衡定数と $K f$ はそれぞれ、

$$
\begin{aligned}
& K_{\mathrm{eq}}=1.62 \times 10^{-10}, \\
& K_{f}=1.0 \times 10^{-14}\left(\mathrm{~m}^{3} / \mathrm{sec} \cdot \mathrm{mol}^{3}\right)
\end{aligned}
$$

であり、式(2)は

$$
\begin{aligned}
& K_{\text {eq }}=1.8 \times 10^{-13}, \\
& K_{f}=1.0 \times 10^{-11}(1 / \mathrm{sec})
\end{aligned}
$$

である ${ }^{6)}$。

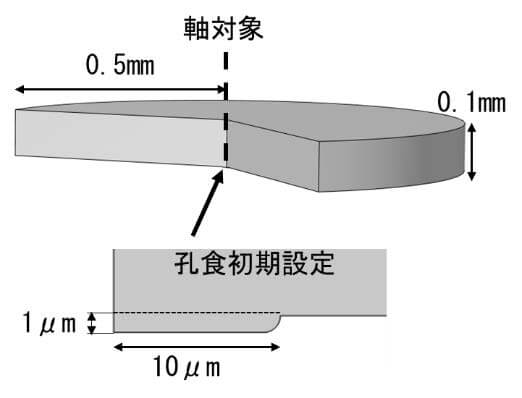
図1. 計算モデルの概要

計算は、軸対称 2 次元モデルを用いて行った。モデルの外観を図 1 に示す。初期の孔食として 半径 $10 \mu \mathrm{m}$、深さ $1 \mu \mathrm{m}$ の形状を設定し、この領域が孔食として成長していく過程を計算した。計算に用いた分極曲線を図 2 に示す。不働態のアノード分極曲線は $3.5 \% \mathrm{NaCl}$ 水溶液での実測値を 用いた。溶液の $\mathrm{pH}$ も実測値 5.5 とした。
孔食部のアノード分極曲線は $\mathrm{Li}$ ら $^{5)}$ の測定値の中で中間的な時間のものを採用した。不働態部のカソード分極曲線は溶存酸素の還元反応のターフェル式とし、平衡電位 $\left(E_{\mathrm{eq}}\right)$、交換電流密度$(i_{0})$ターフェル勾配${A}$はそれぞれ、

$$
\begin{aligned}
& \mathrm{O}_{2}+2 \mathrm{H}_{2} \mathrm{O}+4 e^{-} \rightarrow 4 \mathrm{OH}^{-}, \\
& E_{\mathrm{eq}}(\mathrm{V} v s . \mathrm{SHE})=1.228-0.059 \times \mathrm{pH}, \\
& i_{0}\left(\mathrm{~A} / \mathrm{m}^{2}\right)=1.8 \times 10^{-8}, \\
& \mathrm{A}(\mathrm{V} / \text { decade })=-0.12
\end{aligned}
$$

とした ${ }^{7)}$ 。電極は SUS304 鋼で、密度 $8.03\left(\mathrm{~g} / \mathrm{cm}^{3}\right)$ 、モル重量は $55.34(\mathrm{~g} / \mathrm{mol})$ 、溶解時の電気当量 $(\mathrm{z})$ は 2.2、溶解は、Fe:0.716, Cr:0.197, Ni:0.087 のモル比で溶解するとした。

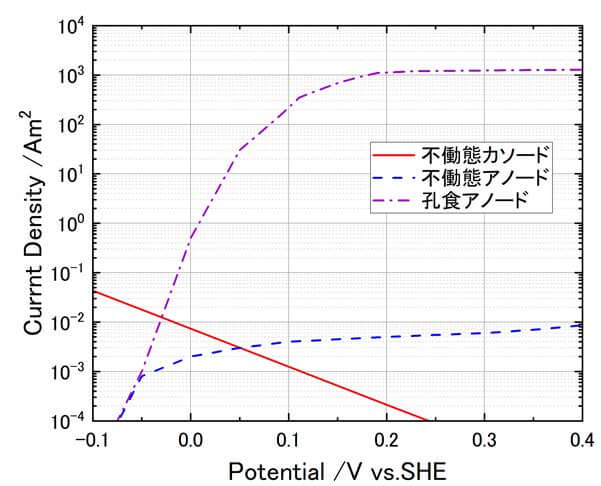
図2. 分極曲線

本書では、SUS304 鋼の孔食のシミュレーション手法を示すモデルおよび、2 章以後に図 3 と 図 4 の解析結果を作成する手順を示した。
計算は $1800 \mathrm{sec}$ まで実施した。孔食部の形状変化を初期値と比較して、図 3 に示す。孔食が半球状に進行する形状変化が計算で精度よく再現されている。

図3. 孔食部の形状変化　A:初期、B:1800sec

また、孔食入口の $\mathrm{pH}$ 変化を図4に示す。孔食の成長とともに $\mathrm{pH}$ が低下していることが計算されている。孔食内部では溶解した$\mathrm{Cr}^{3+}$イオンの加水分解反応で $\mathrm{pH}$ が下がっていくが、孔食内部の$\mathrm{H}^{+}$イオンの濃度上昇と共に外部へ拡散するので極端に低下するものではない。

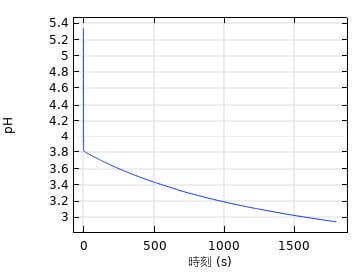
図4. 孔食入口のpH変化

参考文献

1) 久松敬弘、防蝕技術、21,504-512(1972).
2) 佐藤教男、材料と環境、45,731-745(1996).
3) 矢代 仁、千葉俊朗、材料と環境、56,101-111(2007).
4) 鈴木紹夫、北村義治、防蝕技術、17,535(1968).
5) T.Li、 J.Wu、 G.S.Frankel、 Corrosion Science、182,109227(2021).
6) 腐食防食協会編、「腐食防食ハンドブック」CD-ROM版、丸善、付録、代表的な電位-pH図.
7) 腐食防食協会編、「金属の腐食防食Q&A電気化学入門編」、丸善、p.59(2002).

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。