ガス・水道・工場などのパイプライン、地下タンク、基礎杭など広範囲に防食技術が活用されている。電気防食には、マグネシウム合金陽極を使用した流電陽極方式や、直流電源装置を使用した外部電源方式がある。
流電陽極方式はマグネシウム合金陽極または亜鉛合金陽極が用いられる。通常、自然電位がよりマイナスの値を示すマグネシウム合金が高い土壌抵抗率の環境で有効であるので用いられる。流電陽極方式の電気防食システムの設計は、通常、定常状態によってシステムの耐用年数の間に設計パラメーターが一定であると見なされている。しかしながら、実験的観察により、電気防食は過渡的過程であることが分かっている。これによって、実際には事前に設計したパラメーター値から逸脱する可能性があり、時間にかけて埋設物の腐蝕保護は不十分になる。
新設の地下貯蔵タンクの腐蝕保護は防食電流密度を選定しタンクの面積によって、所要防食電流を算出する。それによって、要求される陽極の寸法と数は要求される寿命と陽極タイプによって選定される。そこで本例題は、地下貯蔵タンクの保護面によって電気防食を実現できる陽極の寸法と数を算出し、地下貯蔵タンクの保護面の電位分布変化、過渡的な犠牲陽極の寿命などを検討する。
電気防食システム容量は次式で表される1)。
\(Q_{cp}=I_{cp}×t_f\) (1)
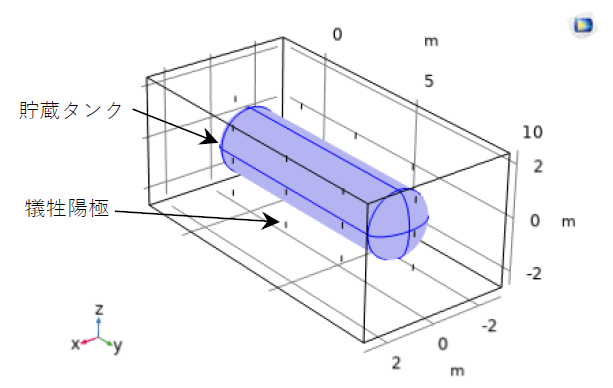
ここで\(Q_{cp}\)は電気防食システム容量、\(I_{cp}\)は要求される防食電流、\(t_f\)は定格寿命である。図1に示した長さ8m、直径2.5mである地下貯蔵タンクのモデル表面積は76.4m2である2)、電気防食システムにおけるカソード表面に酸素還元反応に満たす電流密度は10mA/m2が必要であるため、\(I_{cp}\)=0.764Aである。\(t_f\)=30yrであり、\(Q_{cp}\)は22.9A-yrになる1)。
要求される犠牲陽極の質量は式(2)で求まる。
\(m_a=Q_{cp}/(Q_a×E×U)\) (2)
ここで\(m_a\)は犠牲陽極の質量、\(Q_a\)は犠牲陽極の理論容量、\(E\)は電流効率、\(U\)は利用率である。犠牲陽極の特性は表1に示す。図1に示した直径16cm、長さ24.4cmである円筒形の陽極を考慮する。個数は24である。100mVの陰極分極基準によれば、貯蔵タンクの保護面における-0.8V以上の電位を示す領域は完全に保護されることは知らせている1)。これによって、図1に示したように犠牲エッジ陽極の分布は地下貯蔵タンクの腐蝕保護を完全に実現するように設定される。
| Material | Theoretical (A-hr/kg) | Current efficient | Utilization factor | Equilibrium potential (V \(vs\) CSE) | Density (kg/m3) |
| Magnesium High Potential | 2205 | 50% | 85% | -1.75V | 1820 |
計算は、3次元モデルを用いて行った。COMSOL腐食解析モジュールの陰極防食インターフェースを使って、犠牲エッジアノードの設定は以下のように示される。
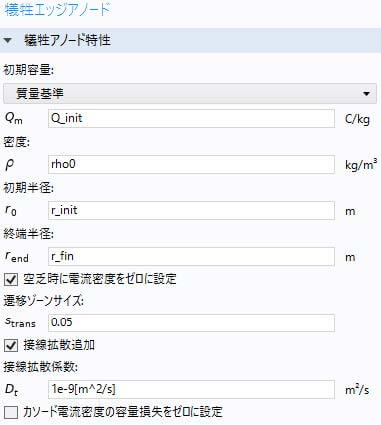
犠牲エッジ陽極ノードでは、腐蝕保護用の棒状の溶解金属電極をモデル化し、3Dジオメトリのエッジに定義される。電気化学反応はエッジの周りの特定の半径で考慮される。犠牲エッジ陽極の半径\(r\)と容量\(Q\)は次式で求められる。
\(\frac{dQ}{dt}=∇_t・(-D∇_tQ)-i_{\rm tot,edge}\)
\(r=\sqrt{\frac {Q}{Q_0}\langle r^2_0-r^2_{end}\rangle +r^2_{end}}\) (3)
ここで\(Q_0\)は初期容量、\(D\)は拡散係数、\(i_{\rm tot,edge}\)犠牲エッジ陽極の総界面電流密度である。下付き文字\(t\)はエッジ接線方向を意味する。腐食により犠牲エッジ陽極が減肉するとともに エッジに沿って渡された電荷の総量を追跡する。初期容量はエッジ初期半径と一致している。エッジ終端半径に達すると、容量はゼロになると設定される。
土壌抵抗率は40 Ω・mとする1)。カソードとアノードの電極表面反応は、カソードにターフェル式、アノードに線形化バトラーボルマー式を利用する。計算用のパラメーターは表2に示す。
| Electrode | Expression | Exchange current density (A/m2) | Tafel slope (V \(vs\) CSE) | Anodic and cathodic transfer coefficients | Equilibrium potential (V \(vs\) CSE) |
| Cathode | Tafel | 0.001 | -0.16 | – | -0.7V |
| Anode | Linearized Butler-Volmer | 0.1 | – | 0.5, 0.5 | -1.75V |
本書では解析モデルおよび、図2と図3の解析結果を作成する手順を示した。
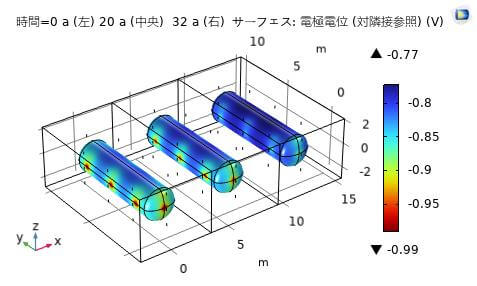
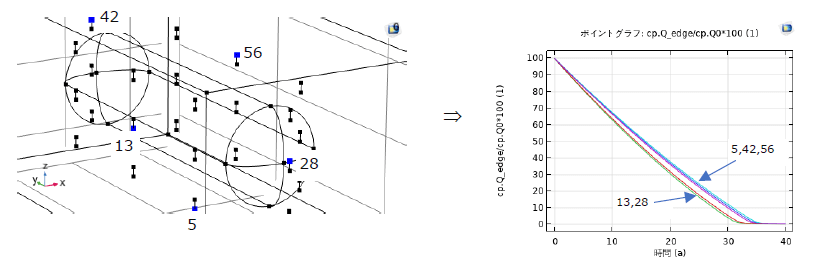
計算は40yrsまで実施した。電極電位を図2に示す。32yrs後の電極電位は、-0.8Vに不満になった箇所があるため、腐蝕保護は不十分であると考えられる。犠牲エッジ陽極の容量の経時変化を図3に示される。貯蔵タンク表面に近づいたエッジ陽極の容量は貯蔵タンク表面に離れたエッジ陽極より3yrs早く、32yrsに初期容量の1%になり、枯渇したことが示された。
参考文献
1) A. Mansouri, A. E. Binali, N. Khan, et al., Three-dimensional modeling of in-ground cathodic protection systems with deforming anodes, Sci. Rep.11, 2021: 1894.
2) M. Attarchi, A. Brenna, M. Ormellese, Cathodic protection design optimization of a buried vessel by FEM simulation, Mater. Corros. 71, 2020: 1651-1659.
3) B. N. Popov, S. P. Kumaraguru, Handbook of Environmental Degradation of Materials,Cathodic Protection of Pipelines, 2012:771–798.
*該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。