近年、全固体リチウムイオン電池の研究がさかんに行われている。電解液を用いた従来のリチウムイオン二次電池との違いは固体電解質である。全固体リチウムイオン電池では、電極活物質内のLiが固固界面における挿入・脱離反応および固体電解質中のLi⁺が輸送して、対極へ輸送されることで充放電が実現される。固体電解質におけるLi⁺は格子欠陥を介してホッピングして移動する。単一イオン電解質とも呼ばれる。電荷的中性条件に従い、固体電解質内のLi⁺濃度は

\(\frac {∂c_l}{∂t}=0\)

である¹⁾。

全固体電池はバルク型全固体電池と薄膜型全固体電池に大別されている。この計算例は、単一イオン伝導性電解質理論に基づいて、COMSOL Multiphysics®によるバルク型全固体電池の解析を行う。放電曲線の計算結果を試験値と比較することで、単一イオン伝導性電解質理論がバルク型全固体電池の解析に適することを考察する。

本書では解析モデルおよび、図2の解析結果を作成する手順を示した。

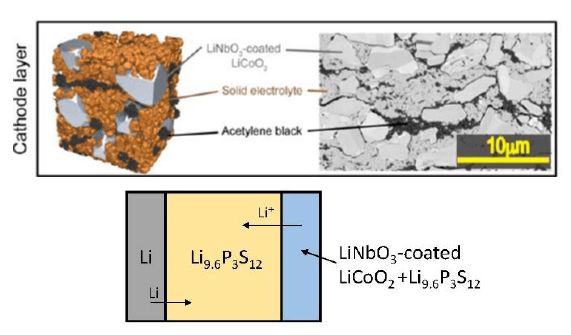
計算ジオメトリは、図1に示すような、正極をLiNbO₃-LiCoO₂、負極をLi、固体電解質をLi_9.6P₃S₁₂とする全固体電池の1Dベンチマークモデルである。正極におけるリチウム挿入脱離反応は、以下のように考慮される。

\({\rm Li}_{1-x} {\rm CoO}_2+x{\rm Li^+}+xe^-{{\underrightarrow {discharge}}\atop{\overleftarrow {charge}}}\rm LiCoO_2\)

この電極反応に対するバトラー・ボルマー式は以下のように示される。

\(i_{\rm loc}=i_0 \left\lbrack {\rm exp}\left( \frac {α_aFη}{RT}\right)-{\rm exp}\left( \frac {-α_cFη}{RT}\right)\right\rbrack,~i_0=i_{0,ref}(T)(\frac {cs}{cs,{\rm ref}})^{α_c}(\frac {c_{s,{\rm max}-cs}}{c_{s,{\rm max}}-c_{s,{\rm ref}}})^{α_a,}\)

\(c_{s,{\rm ref}}=c_{s,{\rm max}}/2\)

ここで、\(i_{\rm loc}\)は電荷移動反応電流密度、\(α_a\)と\(α_c\)はそれぞれアノードとカソードの電荷移動係数、\(F\)はファラデー定数、\(R\)は気体定数、\(T\)は温度である。\(η=Φ_s−ΔΦ_{\rm s,flim}−Φ_l−E_{\rm eq}\)は過電圧であり、電極電位\(Φ_s\)から 電解質電位\(Φ_l\)平衡電位\(E_{\rm eq}\)および薄膜電圧\(ΔΦ_{\rm s,flim} \)を引いたもので定義される。\(i_0\)は交換電流密度 \(i_{\rm 0,ref}\) はNernst式で示した基準平衡電位に対する交換電流密度である。\(c_s\)は正極内のLi濃度、\(c_{s,{\rm max}}\)はLiの最大濃度である。

LiCoO₂電極活物質粒子表面のLiNbO₃薄膜電圧\(ΔΦ_{\rm s,flim}\)の計算は以下の設定で行われる。

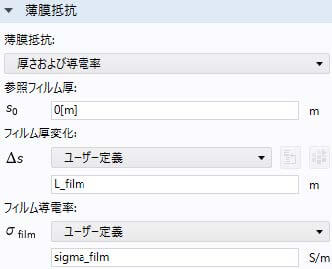
Li負極表面の電極反応は次式で考慮される。

\({\rm Li}{{\underrightarrow {discharge}}\atop{\overleftarrow {charge}}}{\rm Li^+}+e^-\)

バトラー・ボルマー式は以下のように示される。

\(i_{\rm loc}= i_0 \left\lbrack {\rm exp}\left( \frac {α_aFη}{RT}\right)-{\rm exp}\left( \frac {-α_cFη}{RT}\right)\right\rbrack,~i_0=i_{0,ref}(T)\)

LiCoO₂電極における活物質粒子中のLi輸送計算は電池の空間次元の上にCOMSOLの余剰次元1Dで行われる。

\(\frac {∂c_s}{∂t}+∇・(-D_s∇c_s)=0\)

\(\eqalign{ \frac {∂c_s}{∂_r}|_{r=0}&=0\cr
-D_s \frac {∂c_s}{∂r}|_{r=1}&=-i_{loc}/F}\)

ここで、\(D_s\)はLi拡散係数、\(r\)は余剰次元1Dの正規化された座標である。\(r=0\)は活物質粒子中心、\(r=1\)は活物質粒子表面と表される。

電解質と正極内の電流分布は以下の電流保存式を解く。

\(\eqalign{
∇・{\bf i}_l=Q_l&,~∇・{\bf i}_s=Q_s\cr
{\bf i}_l=-σ_l∇Φ_l&,~{\bf i}_s=-σ_s∇Φ_s}\)

ここで、\(σ_l\)と\(σ_s\)はそれぞれ電解質と正極の導電率、\(Q_l\)と\(Q_s\)はソース項である。

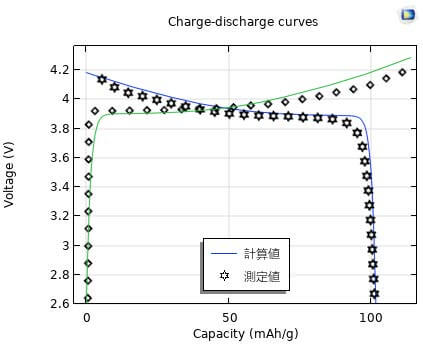
図2にバルク型全固体電池のベンチマーク解析結果を示している。充放電曲線の計算値は試験値²⁾と一致したことで、単一イオン伝導性電解質理論がバルク型全固体電池の解析に適することは明らかにされた。

参考文献

1) N. Wolff, F. Roder, U. Krewer, Model based assessment of performance of lithium-ion batteries using single-ion conducting electrolytes, Electrochim. Acta, 284(10), 2018: 639-646.
2) Y. Kato, et al., High-power all-solid-state batteries using sulfide superionic conductors, Nature Energy 1, 2016: 16030.
3) P. Braun, Assessment of all-solid-state lithium-ion batteries, Journal of Power Sources, 393, 2018: 119–127.
4) H. Yu, et al., Lithium-conductive LiNbO3 coated high-voltage LiNi0.5Co0.2Mn0.3O2 cathode with enhanced rate and cyclability, Green Energy & Environment, 7(2), 2022: 266-274.

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。