予測・評価技術として活用可能なシミュレーション技術は、近年の製造業における開発において重要な役割を果たしている。リチウムイオン二次電池のシミュレーションでは、M. Doyleら¹⁾がイオン種の輸送方程式と電気化学反応を連成して解析する一次元モデル（Newmanの擬似２Dモデルという）を構築して以来、これは電気化学モデルとして非常に多く応用されてきた。

COMSOLバッテリーデザインモジュールはNewmanモデルを採用している。電極活物質粒子中のLi輸送計算は電池の空間次元の上に追加次元1Dで行われる。

\(\frac {∂c_s}{∂t}=-∇・(-D_s∇c_s)\)

境界条件は次式 のように定義される

\(\frac {∂c_s}{∂r}|_{r=0}=0、~−D_s \frac {∂c_s}{∂r}|_{r=1}=−R_{\rm LiΘ}\)

ここで\(D_s\)はLiの拡散係数、\(R_{\rm LiΘ}\)はLiのモル流束、\(r\)は追加次元1Dの正規化された座標である。
\(r=0\)は活物質粒子中心、\(r=1\)は活物質粒子表面と表される。図1に示したLi_yCoO₂におけるLi拡散係数\(D_+\)（ここで \(D_s\)を意味する）の試験値は既に報告された²⁾。yはLi化学量論組成である。

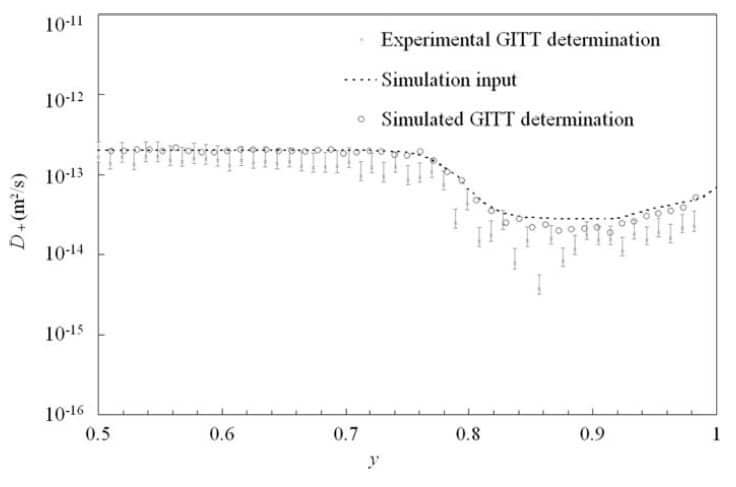
図1に示すLi拡散係数\(D_+(D_s)\)はNewmanモデルに応用する際、電極活物質粒子中のLi輸送計算は明示的な2Dモデルで行われることが必要になる。

本書では解析モデルおよび、図3の解析結果を作成する手順を示した。

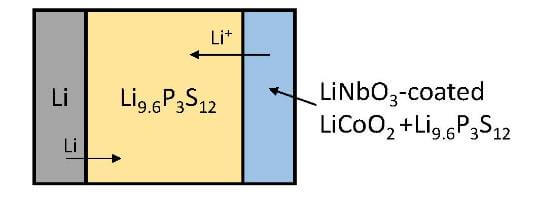
計算ジオメトリは、図2に示すような、正極をLiNbO₃-LiCoO₂、負極をLi、固体電解質をLi_9.6P₃S₁₂とする全固体電池の1Dモデルである。正極におけるリチウム挿入脱離反応は、以下のように考慮される。

\({\rm Li}_{1-x}{\rm CoO_2}+x{\rm Li^+}+xe^-{{\underrightarrow {discharge}}\atop{\overleftarrow {charge}}}{\rm LiCoO_2}\)

この電極反応に対するバトラー・ボルマー式は以下のように示される。

\(i_{\rm loc}=i_0 \left\lbrack {\rm exp}\left( \frac {α_aFη}{RT}\right)-{\rm exp}\left( \frac {-α_cFη}{RT}\right)\right\rbrack,~i_0=i_{0,ref}(T)(\frac {cs}{cs,{\rm ref}})^{α_c}(\frac {c_{s,{\rm max}-cs}}{c_{s,{\rm max}}-c_{s,{\rm ref}}})^{α_a,}\)

\(c_{s,{\rm ref}}=c_{s,{\rm max}}/2\)

ここで\(i_{\rm loc}\) 電荷移動反応電流密度、\(α_a\)と\(α_c\)はそれぞれアノードとカソードの電荷移動係数、\(F\)はファラデー定数、\(R\)は気体定数、\(T\)は温度である。 \(η=Φ_s−ΔΦ_{\rm s,flim}−Φ_l−E_{\rm eq}\) は過電圧であり、 電極電位\(Φ_s\)から 電解質電位\(Φ_l\)平衡電位\(E_{\rm eq}\)および薄膜電圧\(ΔΦ_{\rm s,flim} \)を引いたもので定義される。 \(i_0\)は交換電流密度 \(i_{\rm 0,ref}\) はNernst式で示した基準平衡電位に対する交換電流密度である。\(c_s\)は正極内のLi濃度、\(c_{s,{\rm max}}\)はLiの最大濃度である。

LiCoO₂電極活物質粒子表面のLiNbO₃薄膜電圧\(ΔΦ_{\rm s,flim}\)の計算は以下の設定で行われる。

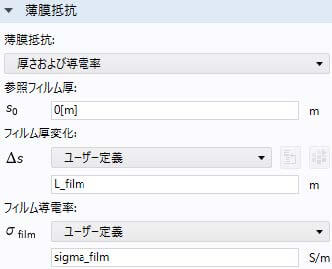
Li負極表面の電極反応は次式で考慮される。

\({\rm Li}{{\underrightarrow {discharge}}\atop{\overleftarrow {charge}}}{\rm Li^+}+e^-\)

バトラー・ボルマー式は以下のように示される。

\(i_{\rm loc}= i_0 \left\lbrack {\rm exp}\left( \frac {α_aFη}{RT}\right)-{\rm exp}\left( \frac {-α_cFη}{RT}\right)\right\rbrack,~i_0=i_{0,ref}(T)\)

電解質と正極内の電流分布は以下の電流保存式を解く。

\(\eqalign{
∇・{\bf i}_l=Q_l&,~∇・{\bf i}_s=Q_s\cr
{\bf i}_l=-σ_l∇Φ_l&,~{\bf i}_s=-σ_s∇Φ_s}\)

ここで、\(σ_l\)と\(σ_s\)はそれぞれ電解質と正極の導電率、\(Q_l\)と\(Q_s\)はソース項である。

電極活物質粒子中のLi輸送計算はCOMSOLのPDEモード：一般形式PDEで行われる。
下図に示した「線形押出し」機能によって、Li輸送計算の２Dモデルはリチウムイオン電池解析の1Dモデルとカップリングされる。

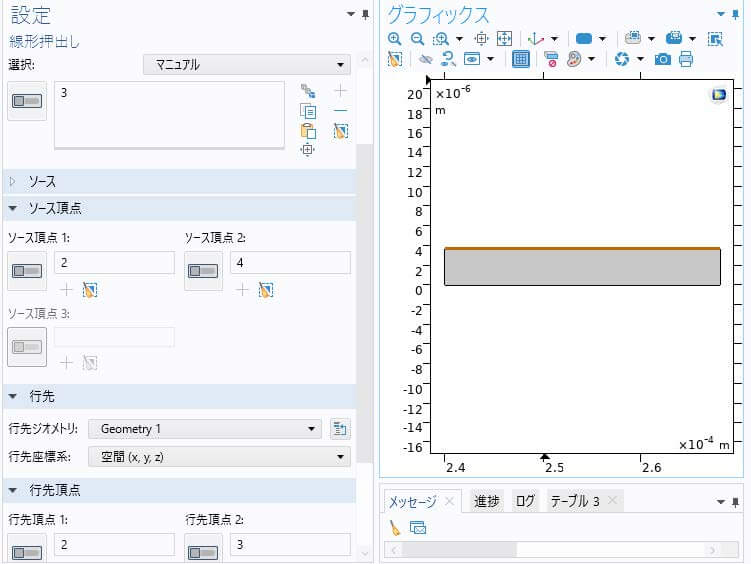
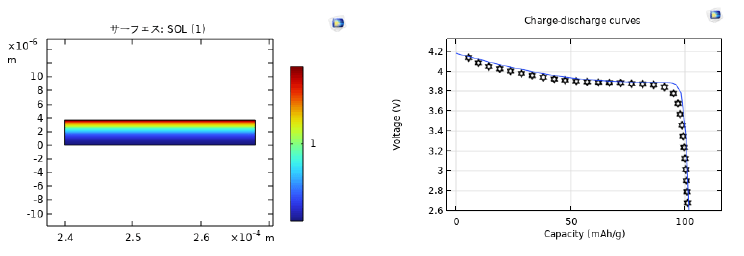
図3(a)にLi/Li_9.6P₃S₁₂/LiNbO₃-coated LiCoO₂とする全固体電池の放電後の正極SOL(State Of Lithiation)を示している。得られた放電曲線は試験値³⁾と一致したことで、本モデルに提案した明示的な2Dモデルの有効性は検証された。

参考文献

1) M. Doyle, J. Newman, A. S. Gozdz, C. N. Schmutz, J.-M. Tarascon, Comparison of modeling predictions with experimental data from plastic lithium ion cells, J. Electrochem. Soc., 143(6), 1890 (1996).
2) S. D. Fabre, D. Guy-Bouyssou, P. Bouillon, F. Le Cras, C. Delacourt, Charge/ discharge simulation of an all-solid-state thin-film battery using a one-dimensional model, J. Electrochem. Soc., 159, A104 (2012).
3) Y. Kato, et al., High-power all-solid-state batteries using sulfide superionic conductors, Nature Energy 1, 2016: 16030.

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。