近年の高度情報化社会及び工業化社会における電力需要の増大に伴い、安定した電力供給が求められている。しかしながら、電気設備においては、 静電気によって障害や災害(障災害)が発生することがある1)。さらに、電気・エネルギー機器や電力ケーブルなどに対しては、省電力化、小型化、高性能化、高信頼性化などの過酷な条件が求められているのが現状である。静電気による障災害を防止するためには、電気絶縁評価が不可欠である。
大気圧での空気絶縁破壊現象については古くから多くの研究が行われてきたが、実験の代わりに数値計算による空気ギャップの絶縁破壊電圧の予測は高電圧工学分野に長い間求められている目標である。 気体放電の基礎理論―タウンゼント理論 ・ ストリーマ理論に基づく電気絶縁評価手法に関しては、Warneらがタウンゼントの電離係数の積分手法を提案している2)。しかしながら、タウンゼントの電離係数を積分する軌道は電気力線なので、不平等電界において追跡することは困難である。
そこで本例題は、粒子追跡法を応用し、電気力線を荷電粒子の軌跡により追跡し、タウンゼント理論・ ストリーマ 理論に基づく絶縁破壊評価を実現できた。
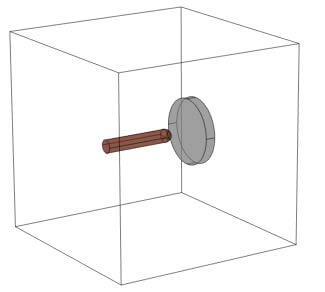
計算、 図1に示したように大気圧での棒-平板電極間の空気ギャップの3Dモデルを扱った。棒-平板電極間の距離は3cmである。棒電極の半径は1cm、円形とした平板電極の半径は5cmである。
本書では解析モデルおよび、図2と図3の解析結果を作成する手順を示した。
大気中では、 電極間に高電圧印加によって電界が発生した時、初期電子(宇宙線などにより生成された)が加速され、衝突電離(α作用とよぶ)を起こし、電界方向(x方向)の電子数変化は次式で記述される。
\(n_e=n_0e^{αx}\) (1)
ここで、\(x\)は電子の移動距離、\(n_0\)は\(x=0\)での初期電子数、\(α\)はタウンゼントの電離係数である。
タウンゼント放電開始条件は
\(γ(e^(αd)-1)=1\) (2)
となる。一方、圧力が高く\(pd\)が大きい領域においてタウンゼント理論は実際の現象と一致しなくなる。これは作用を必要とせず、α作用と光電離作用および空間電荷電界による小さな二次電子なだれが放電を起こしているストリーマ理論という。ストリーマ放電開始条件は
\(αd≅K\)
である。実験結果によって\(K=15~20\)で火花条件を満たす2)。
不平等電界に対して、本例題では、放電無し、タウンゼント放電およびストリーマ放電の3種類の絶縁レベルに分けられ、次式で表される2)。
\(\eqalign{{\rm 放電なし:} & \int_D^0 αds<ln(1+ \frac1γ)\cr
{\rm タウンゼント放電:} &\int_D^0 αds≥ln(1+ \frac1γ)\cr
{\rm ストリーマ放電}: &\int_D^0 αds≥17.7+ln(D/1{\rm cm})}\) (4)
ここで、\(α=α(E/N)\)である。\(E\)は電界、\(N\)は気体の数密度である。式(4)に示した絶縁レベルを評価する絶縁破壊インジケーター変数と定義される。
式(4)に示した電気力線の軌跡\(s\)は粒子追跡法によって求められる。電場中の荷電粒子の運動方程式は
\(m \frac {du}{dt}+mνu=qE\)
で示される4)。ここで、\(u\)はドリフト速度、\(m\)は質量、\(ν\)は衝突周波数、\(E\)は電場、\(q\)は電荷である。これを解けば、\(u=qE/mν \lbrace 1-{\rm exp}(-νt) \rbrace \)となるが、定常解は
\(u=\frac {q}{mν}E≡μE\)
ここで\(μ≡\frac {q}{mν}\)は移動度である。
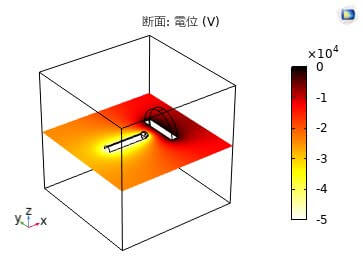
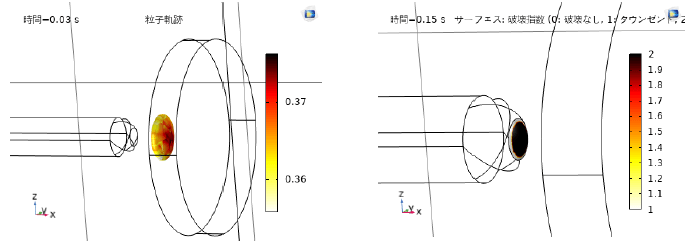
図2は棒-平板電極間の電位分布である。平板電極を接地し、棒電極に-50kVを印加する。棒-平板電極間の電気力線の分布を示す粒子の軌跡および絶縁破壊インジケーターを図3に示す。
参考文献
1) 崔光石 , 遠藤雄大 静電気による爆発・火災および防止対策 セイフティ ・ エンジニアリング 2017
No.187: 10-15.
2) L.K. Warne, R.E. Jorgenson,S.D. Nicolaysen, Ionization coefficient approach to modeling breakdown in non-uniform geometries.Sandia Report, 2003.
3) 秋山秀典 高電圧パルスパワー工学 オーム社, 2003 19-29.
4) 電気学会編集 放電 ハンドブック.オーム 社, 1991 46-66
*該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。