ガラスの高周波誘導加熱攪拌は、放射性廃棄物の溶融固化、ガラスファイバーのリサイクル等の分野において、十分な溶融と組成の均一化を得るために行なわれている。しかしながら溶融シリケートガラスの粘度は高く、また導電率も十分高くないため、誘導攪拌は必ずしも容易ではない。ここでは、ガラスとする非金属高温融体の誘導加熱攪拌に関して基礎的な理解を得るために、電磁誘導加熱撹拌に関するシミュレーションを行う。

一般に金属融体の場合、数10kHz程度の高周波が用いられているが、本研究では非金属融体に電磁誘導加熱撹拌を適用することを目的に、COMSOL Multiphysicsを用いて400kHzの高周波による導電性ガラス融体の誘導加熱を計算し、融体における磁場、温度、流速および電磁力分布を得た。

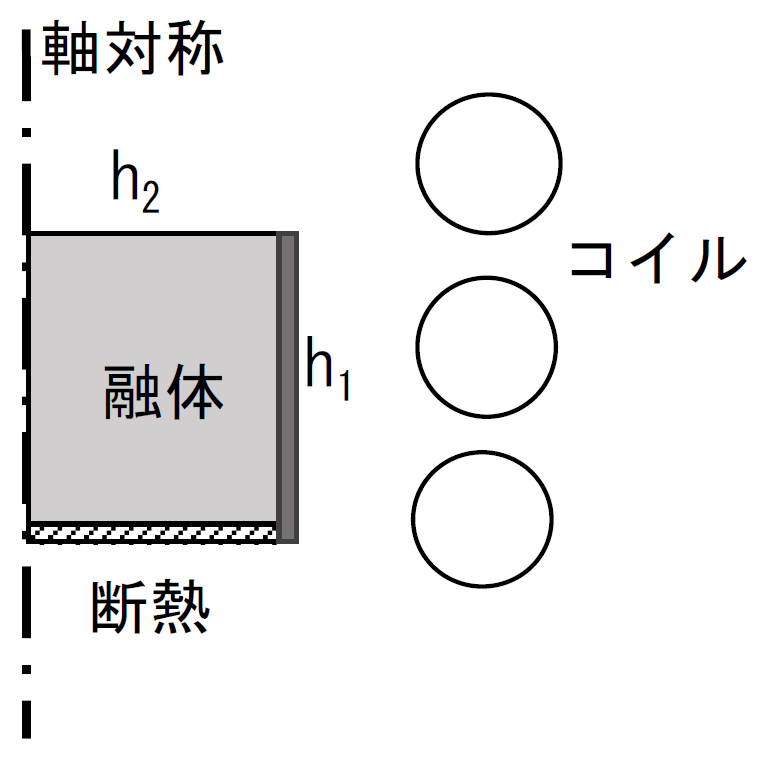
計算モデルは軸対称二次元モデルであり、融体の計算領域は図1に示されている。融体の周辺を空気とする。融体の計算領域は半径22mm・高さ22mmの円筒形状で、マルチターンコイルに対して400kHzの高周波電流を印加し、それにより発生する磁場を解析する。この磁場が融体内に入り誘導電流を生じ、それと共に生じるローレンツ力を計算する。本計算においては電磁場解析、流動、および伝熱の連成計算が行われている。

電磁場解析は、以下に示すベクトルポテンシャル\(\text{A}\)を用いて解析を行われる。式(1)と(2)に示すように \(\text{A}\) を求めることにより、融体表面に生じる誘導電流 \(\text{J}\) や磁場 \(\text{B}\) を求めることになる。金属の場合と異なり、ガラス融体の導電率が1×10²S/mオーダーであるため、式(3)で電磁場の浸透距離は、数cm程度にも及ぶ。したがって金属の場合とは異なり、表皮電流という状態とは異なっている。ローレンツ力 \(f_L\) は式(4)により求められるが、これは主に軸中心軸に向かって作用することになり、ピンチ力(ローレンツ力)として流動を駆動する。

\(\begin{align}
& \nabla^2-\frac{\partial^2}{\partial t^2}A=\mu_{m}J \tag{1}\\
& B=\nabla\times A \tag{2}\\
& \delta=\sqrt\frac{2}{\omega\sigma\mu m} \tag{3}\\
& f_L=J\times B \tag{4}
\end{align}\)

ここで、角周波数\(\omega=2\pi f\)、\(f\)=400kHz、透磁率\(\mu_m=\mu_0\)(真空透磁率)、\(\delta\):表皮厚さ、\(\sigma\):導電率である。

流動と熱移動については、流動Navier-Stokesの式(5)と熱移動の式(6)を連立させて解く。ここで熱移動式における発熱項として誘導電流\(\text{J}\)を用いている。また流動の駆動項としてローレンツ力を与えている。強い流動が生じる場合、流動による磁場分布への影響を考慮しなければならないが、本系においては磁気レイノルズ数\(Re_m\)を評価し、その必要がないことを確認し基礎式の連成関係としては電磁場解析から熱流動解析への一方向となっている。

\(\begin{align}
& \rho(u・\nabla)u=\mu\nabla^2 u-\nabla p+f_L+\rho g \tag{5}\\
& \rho C_p\left(\frac{\partial T}{\partial t}+u・\nabla T\right)=\lambda\nabla^2 T+\frac{J^2}{2\sigma} \tag{6}
\end{align}\)

ここで\(u\):速度、\(rho\):流体密度、\(\mu\):流体粘度、\(p\):圧力、\(g\):重力加速度、\(C_p\):定圧比熱、\(\lambda\):熱伝導度である。

非圧縮性流体では、流体の温度差によって浮力\(F\)を生じるため、ここでは、式(5)に示す重力\(\rho g\)が「ブシネスク近似」とよばれる次式で置き換えられる。

\(\begin{align} F=-\rho_0 g\beta(T-T_0) \tag{7} \end{align}\)

ここで \(\rho_0\):基準温度での密度、\(\beta\):体膨張率、\(T\):温度、\(T_0\):基準温度である。

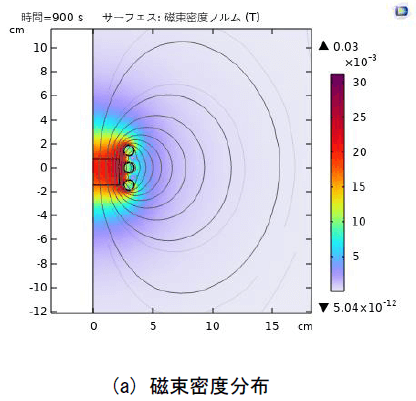
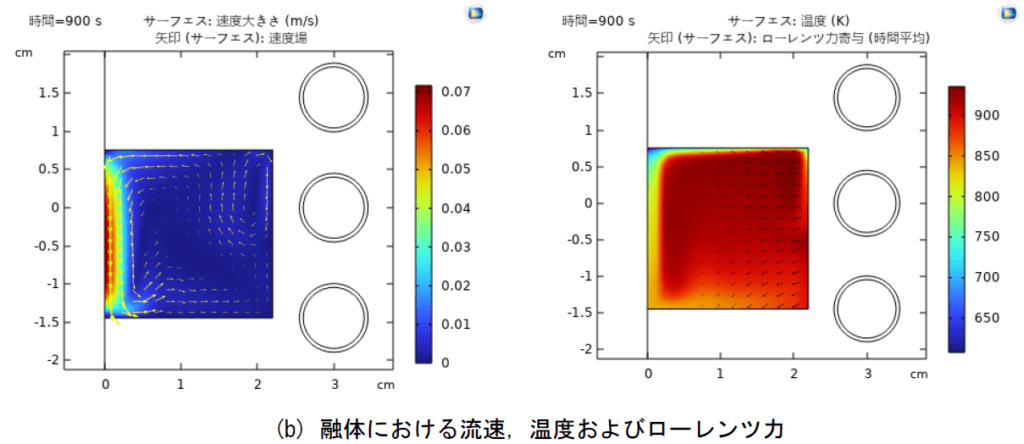
本書では解析モデルおよび、図2の解析結果を作成する手順を示す。

融体は絶縁性のるつぼに入っており、底面には断熱材が敷いてある。このため、流動の境界条件として、側面コイル面と底面は速度0とし、コイル上面は自由表面境界としてCOMSOLの対称性条件を用いて軸方向と回転方向の流れを考慮する。伝熱の境界条件としては図1に示しているが、底面断熱、融体側面(コイル面)と上面とでの伝熱係数h1、h2は実験で求めた冷却曲線をフィッティングする方法で決定した値を代入する。

計算には、コイルに400Aを印加し、電磁加熱時間を15minとした図2に磁束密度、融体内の流速、温度およびローレンツ力を示している。

参考文献

1) N. Yoshikawa, K. Watanabe, T. Igarashi, and S. Komarov, CAMP-ISIJ, Vol. 32 (2019).
2) N. Yoshikawa, K. Watanabe, T. Igarashi, and S. Komarov, Proc. 4th Int. Conf. of Electromagnetic Processing of Materials (EPM2018), CD.

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。