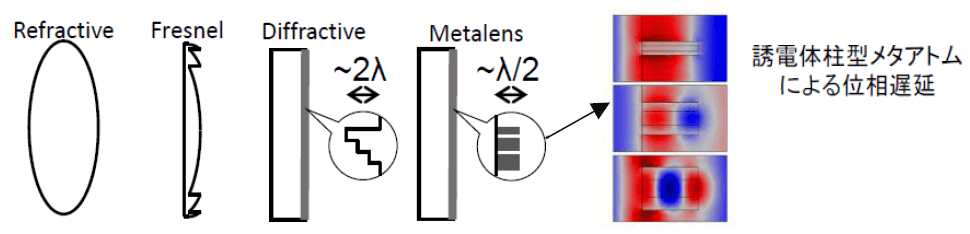
近年、フォトニクスの分野ではメタサーフェス(metasurface)と呼ばれる二次元メタマテリアルの研究の進展が著しい。波長より極めて薄い平面レンズ(メタレンズ)や位相素子(メタホログラム)が実現され、既存の光学素子を超える性能や機能が出せるようになった。メタサーフェスは三次元ナノ加工を必要とするバルクのメタマテリアルより作製がはるかに容易であり、大面積化やフレキシブル化にも適している。また、メタサーフェスには既存の素子が十分ではないテラヘルツ、中赤外、深紫外波長域での光学素子の実現が期待される。特に金属を用いない誘電体メタサーフェスの登場により、長年の課題であった金属メ タマテリアルの持つ損失の問題が解決されたことで、実用化が報告され始めている。メタサーフェスによるメタレンズは、偏光分離イメージングのような新機能や、高NAと高効率の両立などの特徴から、次世代の超薄型素子として期待されている1)。図1に従来レンズとメタレンズとの比較をまとめた。
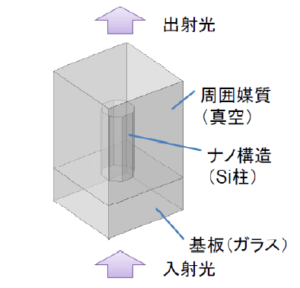
本シミュレーションは、Si誘電体の円柱状導波路の伝搬位相遅延を解析する。設計波長における光透過率と位相差を求める。計算モデルは図 2に示す。
電場の波動方程式は式(1)に示されている。
\(\begin{align}
\nabla^2E_0-\mu_r\epsilon_r k^2_0E_0=0 \tag{1}
\end{align}\)
ここで\(E_0\)は電場、\(\mu_r\)は比透磁率\(\epsilon_r\)は比誘電率、\(k_0\)は波数である。入射光電場\(E\)は次式で定義される。
\(\begin{align}
E(r,t)=E_0 (r)\exp[i(\omega t)] \tag{2}
\end{align}\)
計算には、COMSOL Multiphysicsの波動光学モジュールの電磁波(周波数領域)(ewfd)インターフェースを利用する。光透過率はabs(ewfd.S21)2で評価される。ewfd.S21はCOMSOLのSパラメータであり、Sパラメータの概念図が図3に示されている2)。
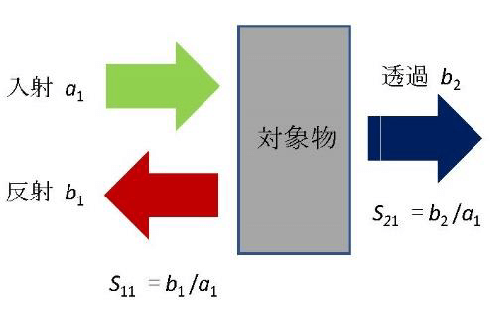
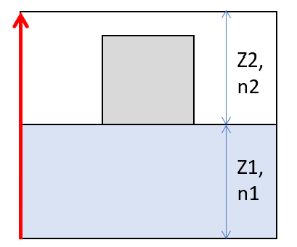
Sパラメータは光の入り口と出口の位相ずれなので、波長が違うと位相差も変わる (波長が短いと位相遅れが生じる)。メタサーフェスを計算するときは、構造間の位相差だけに着目する。ここでは、図1に示す解析領域において、下から光を入射、上から出射、左右は周期境界とする。柱がない場合を位相の基準として、図4に示す光路長が考えられ、柱がないときの光路長は次式で表す。
\(\begin{align}
n_1z_1+n_2z_2 \tag{3}
\end{align}\)
ここで, \(n_1\)と\(n_2\)は媒質の屈折率、\(z_1\)と\(z_2\)は光が進む距離である。よってその時の基準位相は
\(\begin{align}
\phi_0 =-\frac{2\pi}{\lambda_0}(n_1z_1+n_2z_2+)=-k_1z_1-k_2z_2 \tag{4}
\end{align}\)
になる。一般的に書くと、
\(\begin{align}
\phi_0=-\int\frac{2\pi}{\lambda_0}n(z)dz=-\int k(z)dz \tag{5}
\end{align}\)
が得られる。
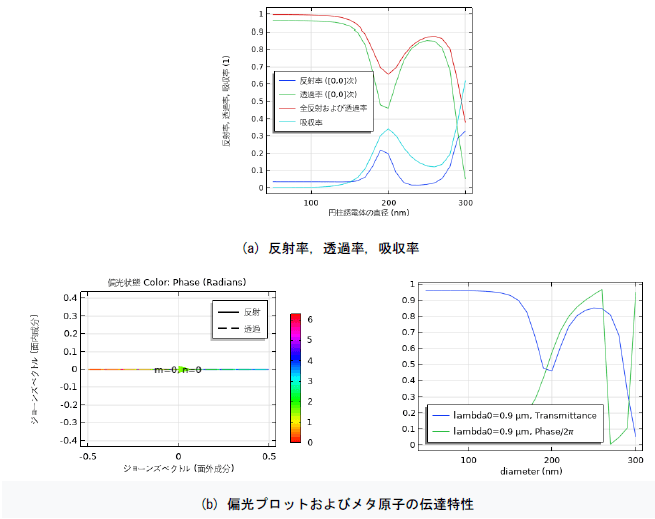
本書では解析モデルおよび、図5の解析結果を得る手順を示す。位相を示すため、COMSOLのIf文およびMod剰余演算 子を利用し、基準位相に対するメタ原子の位相遅れは次式で定義示される。
\(\begin{align}
&\text{if}( \\
~~&\mod(-\phi_0+\pi,2\pi)-\pi-\arg(\text{ewfd.S21})\lt0, \\
~~&\mod(-\phi_0+\pi,2\pi)-\pi-\arg(\text{ewfd.S21})+2\pi, \\
~~&\mod(-\phi_0+\pi,2\pi)-\pi-\arg(\text{ewfd.S21}) \\
&)/(2*\text{pi})
\end{align}\)
ここで、\(\mod(-\phi_0+\pi,2\pi)-\pi\)は\(\phi_0\)の\(-\pi\sim\pi\)への写像, arg(ewfd.S21)は入射光と透過光の位相差、\(+2\pi\)は位相遅れが負なら、正に戻すと意味する。また、基板が吸収性媒質(nが複素数)の場合は\(\phi_0\)が複素数となり、そのため\(\phi_0\)を\(\text{real}(\phi_0)\)として書き換えて\(\phi_0\)の実部を取り出すことになる。
図5に誘電体メタサーフェスの解析結果を示している。メタ原子の透過率と位相\(/2\pi\)をシミュレーション設計解が得られた。
参考文献
1) 岩見健太郎, 誘電体メタサーフェスを用いた可変焦点メタレンズ 精密工学会誌,88巻(2022)5号, pp. 370-373.
2) 藤城義和, Sパラメータ活用術, https://product.tdk.com/system/files/dam/doc/content/emc-guidebook/ja/jemc_basic_03.pdf
*該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。