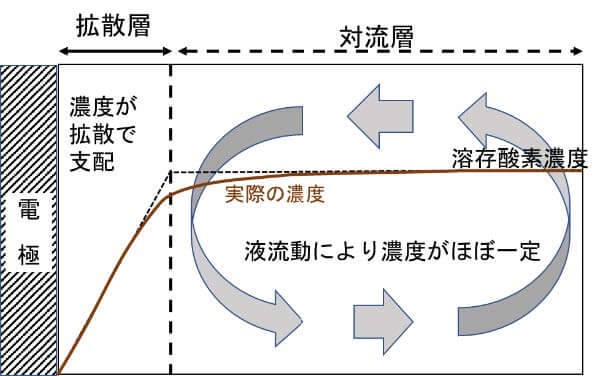
腐食の教科書には、必ずと言っていいほど腐食の拡散支配と拡散層に関する記載がある。前田正雄先生の著書「電極の化学」¹⁾に『電極表面に厚さ\(\delta\)の薄層を考え、化学種の濃度勾配はこの薄膜層にのみ存在し、しかも距離に対して直線的に変化するものとする。この薄層を拡散層と称する』との記載がある。これだけを読むと意味が分かり難いが、水溶液には拡散層と対流層がある。 対流層では溶液の流動があり、化学種の濃度はほぼ一定になっているが、拡散層では溶液の流動がなく、化学種の拡散のみで濃度変化が起きる。例えば電極表面で化学種を還元することで、その濃度がゼロに近づいた場合には、図1に示す様に拡散層にのみ直線的な濃度勾配が生じる。

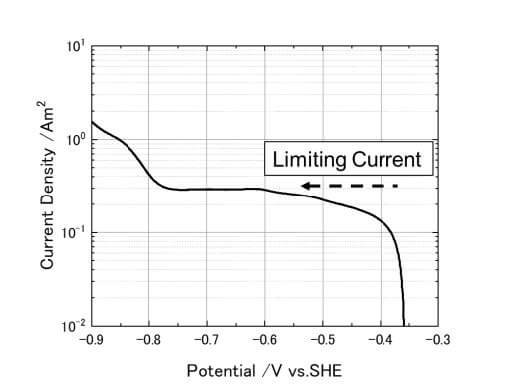
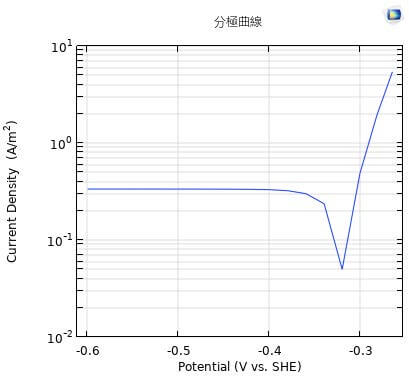
通常の溶液中の腐食現象において、拡散層の影響を強く受けているのが溶存酸素の還元反応である。図2には、0.1mol/m³NaCl水溶液中での炭素鋼のカソード分極曲線の例を示す。-0.5から-0.8V vs. SHEの間でほぼ一定のカソード電流密度が測定される。COMSOLにおける電気化学的計算において、この実測データを数値関数としてカソード電極反応に設定することも可能ではあるが、ここではその原理に従った計算条件の設定法を考える。

電極表面で濃度がほぼ0となる化学種の拡散限界電流値\(i_\lim\)は化学種の拡散係数\(D\)、対流層での化学種濃度\(C_0\)、拡散層厚み\(\delta\)、電極反応の電荷数\(z\)、ファラディ定数\(F\)とすると、(1)式で示される。

\(\begin{align}
i_\lim=\frac{zFDC_0}\delta \tag{1}
\end{align}\)

ここで、溶存酸素の還元反応(2)を考えると、

\(\begin{align}
\rm O_2+2H_2O+4e^-~\rightarrow~4OH^- \tag{2}
\end{align}\)

\(z=4,~F=96500C/eq,~D=1.8\times10^{-5}\rm cm^2/s\)²⁾、流動層の溶存酸素濃度を\(8\text{ppm},~C_0=0.25\rm mol/m^3\)となり、拡散層厚さをよく使われる\(500\rm\mu m\)とすると、\(i_\lim=0.35\rm A/m^2\)を 得る。これは、図2の結果とほぼ一致する値である。

式(2)の反応については、Feを電極とした場合に、カソードターフェル式

\(\begin{align}
&\textbf{平衡電位}& &:~E_\text{eq}=1.228-0.059\rm pH~V~vs.~SHE \\
&\textbf{交換電流密度}& &:~i_0=1.0\times10^{-8}\rm A/m^2 \\
&\textbf{カソード$\rm Tafel$勾配}& &:~b_c=0.130\rm V/decade
\end{align}\)

に従う。ちなみにpH7.0の場合の\(E_\text{eq}\)は0.815V vs. SHEとなる。

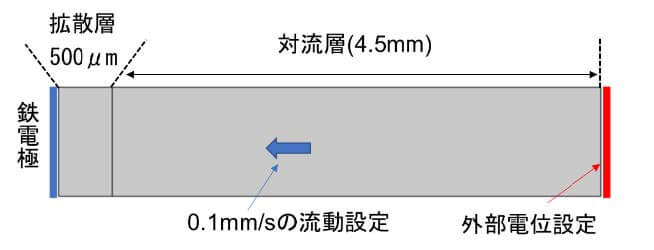
本書では、酸素拡散限界電流の計算手法を示す2次元モデル(図3)および、2章以後に図4と図5の解析結果を作成する手順を示した。

計算をNaCl溶液の濃度として3%(0.51mol/m³)水溶液で行った。アノード反応はアノードターフェル式

\(\begin{align}
&\textbf{平衡電位}& &:~E_\text{eq}=-0.6\rm~V~vs.~SHE \\
&\textbf{交換電流密度}& &:~i_0=6.0\times10^{-8}\rm A/m^2 \\
&\textbf{アノード$\rm Tafel$勾配}& &:~b_\text{a}=0.042\rm V/decade
\end{align}\)

を用いた。溶液中はNa⁺、Cl^–、H⁺、OH^–、O₂の拡散泳動をNernst-Planckの式(3)で計算して連成した。

\(\begin{align}
\frac{\partial c_i}{\partial t}+\nabla・(-D_i\nabla c_i-z_iu_{m,i}Fc_i\nabla\phi_l+c_iu)=R_i \tag{3}
\end{align}\)

ここで、\(c_i,D_i\)はそれぞれの化学種の濃度と拡散係数、\(z_i\)はイオンの価数、\(m_i\)は移動度、\(\phi_l\)は溶液の電位 、\(u\)は溶液の流速、\(R_i\)は反応速度である。

酸素還元反応は、電極表面の酸素濃度に影響を受けるので、拡散層外の濃度と電極表面での濃度比に比例するという (4)の条件を設定した。また、拡散層では液流動を考えないが、対流層では、電極方向に向って流れる0.1mm/secの流動があると設定した⁴⁾。

\(\begin{align}
i_\rm{o_2\_red}~\propto~\rm cO_2\_s/cO_2\_0 \tag{4}
\end{align}\)

ここで、\(i_\rm{o_2\_red}\)は酸化還元反応の電流密度すなわち反応速度、\(\rm cO_2_s\)は電極表面の酸素濃度、\(cO_2_0\)は沖合の酸素濃度である。

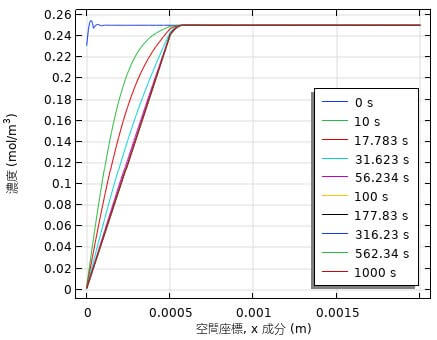
図4には、電極表面からの距離と溶存酸素(DO)濃度との関係を、0.4V vs. SHEの外部電位での結果である。電極表面より500μmまではDOの濃度勾配が形成され、それより沖合では0.25mol/m³(8ppm)で一定値になる。また、DOの分布は約100secで定常値になる。

外部溶液電位を0.26Vから0.6Vまで変化させて電極表面の総電流密度をプロットした結果を図5に示す。総電流密度は電極から溶液内に流れ出る電流の絶対値になるので、いわゆる分極曲線と同じ結果になる。

1) 前田正雄, 電極の化学, 技報堂, 104 (1961).
2) P.Han, D.M.Batels, J.Phys. Chem., 100, 5597-5602 (1996).
3) 腐食防食協会編，金属の腐食防食 Q&A-電気化学入門編, 丸善, 59 (2002).
4) 山本正弘, 材料と環境, 71, 97-100 (2022).

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。