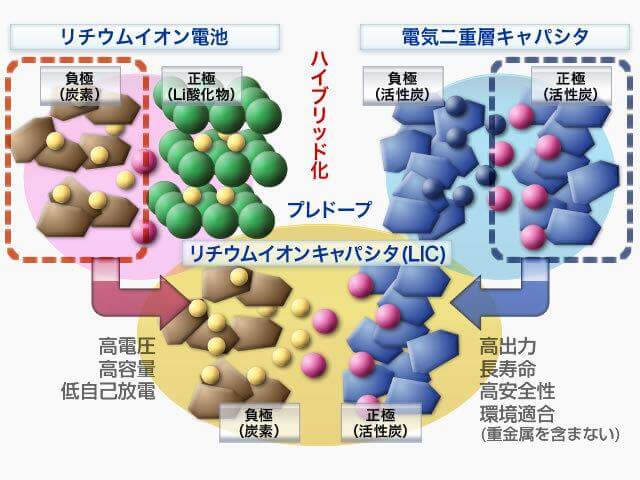
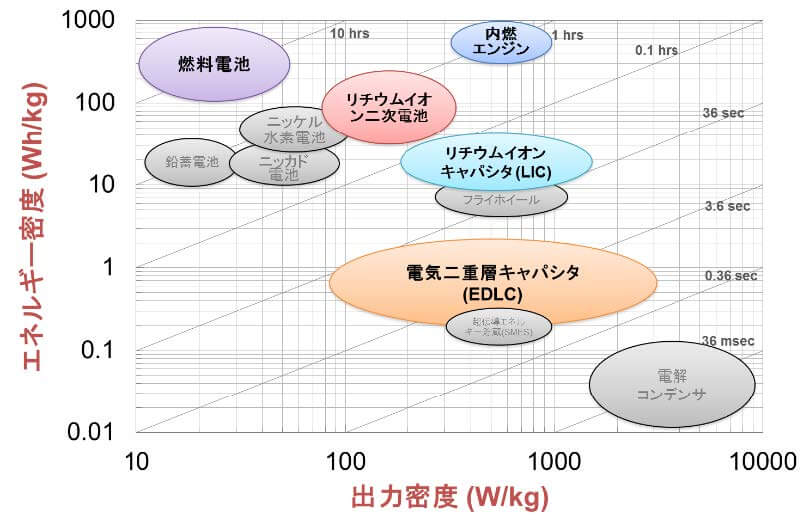
リチウムイオンキャパシタ(LIC)とは、一般的な電気二重層キャパシタの原理を使いながら負極材料としてリチウムイオン吸蔵可能な炭素系材料を使い、そこにリチウムイオンを添加することでエネルギー密度を向上させたキャパシタである。正極と負極で充放電の原理が異なり、リチウムイオン二次電池の負極と電気二重層の正極を組み合わせた構造を持っている。図1はリチウムイオンキャパシタ(LIC)の構造図である。各蓄電デバイスのエネルギー密度と出力密度は図2に示す。

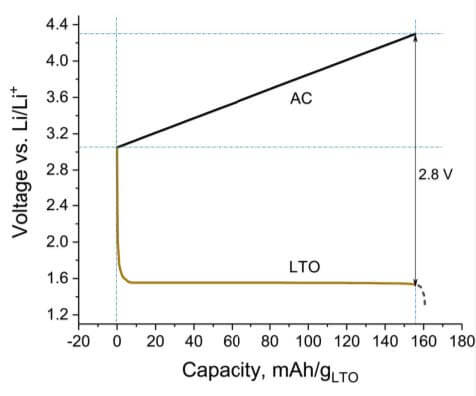
リチウムイオンキャパシタ(LIC)には多くの組み合わせがある。その中に、正極として活性炭(AC)と負極としてLTO(Li₄Ti₅O₁₂)および有機溶媒(1MLiPF₆,EC:DMC)の組み合わせがよく使用される。電極材料の電圧特性は図3に示している¹⁾。
正極(AC)における電気二重層の充放電は式(1)で表現される。

\(\begin{align}
\rm AC+PF^-_6<=>AC^+・PF^-_6+\it e^- \tag{1}
\end{align}\)

負極(LTO)におけるリチウムイオン挿入脱離反応 は式 (2)で表現される。

\(\begin{align}
\rm Li_4Ti_5O_{12}+3Li^++3{\it e}^-<=>Li_7Ti_5O_{12} \tag{2}
\end{align}\)

式(1)に示す電気二重層の 電荷保存は次式で反映される。

\(\begin{align}
j_s=C_{dl}\frac{\partial(\phi_s-\phi_l)}{\partial t} \tag{3}
\end{align}\)

ここで、\(j_s\)は電気二重層の電流密度、\(\phi_s\)と\(\phi_l\)はそれぞれ電極と電解質の電位、\(C_{dl}\)は電気二重層のキャパシタンスである。
式(2)で示されたリチウムイオン挿入脱離反応はバトラー・ボルマー式で計算される。

\(\begin{align}
j_s=i_0 \left\{\exp(\frac{\alpha_aF\eta}{RT})-\exp(\frac{-\alpha_cF\eta}{RT})\right\} \tag{4}
\end{align}\)

ここで、\(i_0\)は交換電流密度、\(\alpha_a\)と\(\alpha_c\)はそれぞれアノードとカソードの電荷移動係数、\(F\)はファラデー定数、\(R\)は気体定数、\(T\)は温度である。\(\eta\)は過電圧を表し、 \(\eta=\phi_s-\phi_l-E_{eq}\)であり、\(E_{eq}\)は平衡電位である。
交換電流密度\(i_0\)は式(5)で定義される。

\(\begin{align}
i_0=F(k_c)^{\alpha_a}(k_a)^{\alpha_c}(c_{s,max}-c_s)^{\alpha_a}(c_s)^{\alpha_c}( \frac{c_l}{c_{l,ref}})^{\alpha_a} \tag{5}
\end{align}\)

ここで、\(k_a\)と\(k_c\)はそれぞれアノードとカソードの反応速度定数、\(c_s\)は負極活物質粒子内のLi濃度、\(c_{s,max}\)はLiの最大濃度、\(c_{l,ref}\)は電解質の参照濃度である。
正極(AC)、負極(LTO)およびセルの容量Q_AC,Q_LTO,Q_cellは次式で定義される。

\(\begin{align}
&{\rm Q_{AC}}&~&:~ C_{dl}a_{v,dl}A_{cell}\delta VL_{AC}\\
&{\rm Q_{LTO}}&~&:~ C_{s,max}\epsilon_{s,LTO}A_{cell}L_{LTO}F\\
&{\rm Q_{cell}}&~&:~ {\rm min(Q_{AC},Q_{LTO})}
\end{align}\)

ここで、\(C_{dl}\)と\(a_{v,dl}\)はそれぞれACのキャパシタンスと比表面積、\(C_{s,max}\)と\(\epsilon_{s,LTO}\)はそれぞれLTOのLi最大濃度と電極固相の体積比率、\(L_{AC}\)と\(L_{LTO}\)はそれぞれACとLTOの厚さである。\(A_{cell}\)はセルの投影面積、\(\delta V\)はACの許容電位範囲である。

本書では解析モデルおよび、解析結果を得る手順を示す。
解析モデルにおけるリチウムイオン輸送計算はバイナリ電解質として高濃度種電解液の輸送理論が利用される。計算ジオメトリは1Dモデルである。
LICの電解質中の電荷キャリアの平均濃度は充放電における両方インと両方アウトのメカニズムによって変化するため、電解質塩の濃度変化の影響はLICの計算に考慮される。計算用の電解質塩の輸送特性への電解質濃度の影響は図4に示されている。

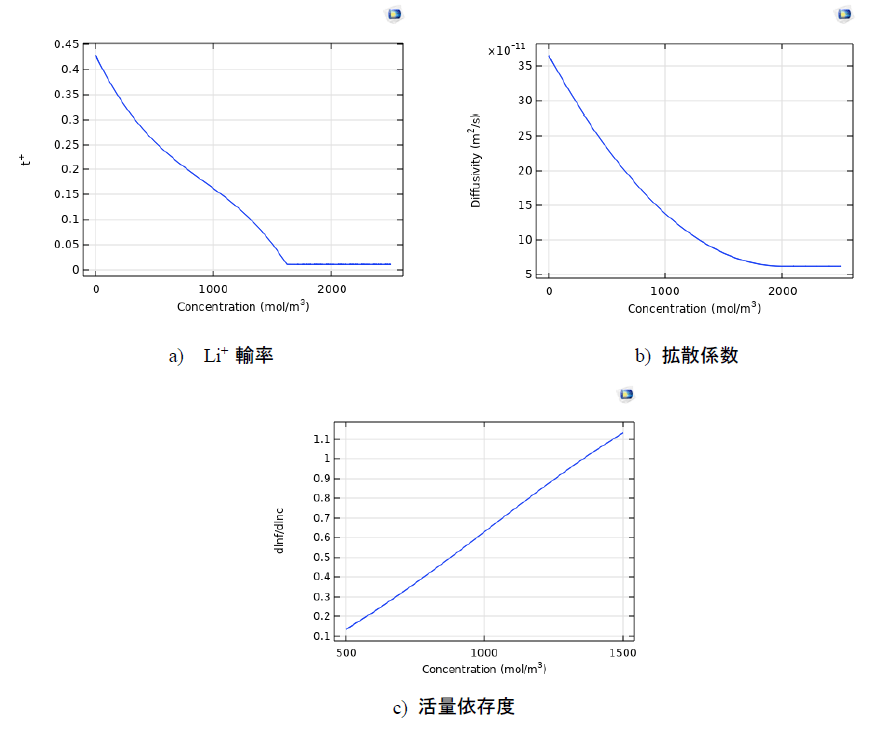
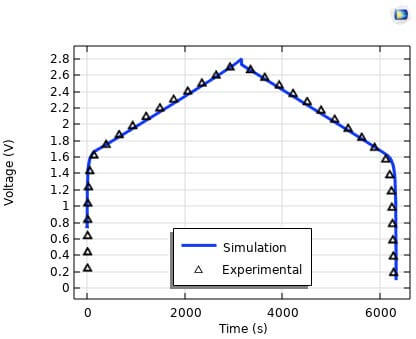
図5はリチウムイオンキャパシタ(LIC)の充放電のベンチマーク計算結果である。
計算値は試験値(記号)²⁾と一致したことで、本書で示された計算理論がリチウムイオンキャパシタ(LIC)の解析に適することを明らかにさせた。

1) G. Madabattula, B. Wu, M. Marinescu, G. Offer, “How to Design Lithium Ion Capacitors: Modelling, Mass Ratio of Electrodes and Pre-lithiation”, J. Electrochem. Soc. 167, 2020: 013527.
2) S. Dsoke, B. Fuchs, E. Gucciardi, M. Wohlfahrt-Mehrens, “The Importance of the Electrode Mass Ratio in a Li-ion Capacitor based on Activated Carbon and Li₄Ti₅O₁₂”, J. Power Sources 282, 2015: 385-393.

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。