ストリーマ放電のシミュレーションについては 古くから報告例がある。しかしながら膨大な計算量による制限から、シミュレーションは1次元、もしくは1.5次元モデルで行われており、ストリーマ放電の特徴の一つである電子輸送の高いペクレ数に対して、数値解析に安定化技術への制限があった。安定化条件を満たさない場合は、電子密度がマイナスになる非物理的な数値のアーティファクトが生じることもある。

ストリーマ放電モデルの作成における重要な部分の一つは計算領域のメッシングである。ストリーマヘッドでの電荷分離層の厚さは数十マイクロメートルのオーダーであるため、このような薄い層をキャプチャできるように非常に細かいメッシュが必要になる。さらに、メッシュは伝搬するプラズマフロントに追従する必要がある。解決方法の1つは適合格子細分化法(AMR法)を使用する¹⁾。それによって、非常に細かいメッシュ(典型的な要素サイズ～10μm)が移動するストリーマヘッドの前に配置され、ストリーマヘッドの後ろのプラズマチャネルに要素サイズ50～70μmのメッシュを生成できる。そこで本例題は、COMSOL MultiphysicsのAMR法による計算方法を示す。

COMSOL MultiphysicsのAMR法では、L2ノルム誤差推定、関数による誤差推定、エラーインジケーターという手法が 提供される²⁾。細分化する格子の割合は

\(\begin{align}
\rho=\frac 1{2^pN}\sum_{i=1,\gamma(i)\ne 0}^N 2^{r(i)} \tag{1}
\end{align}\)

で計算される。ここで、\(N\)はベースメッシュの要素数、\(\gamma\)は格子を細分化する必要となる要素の細分化回数、\(p=\max_i\gamma(i)\)である。

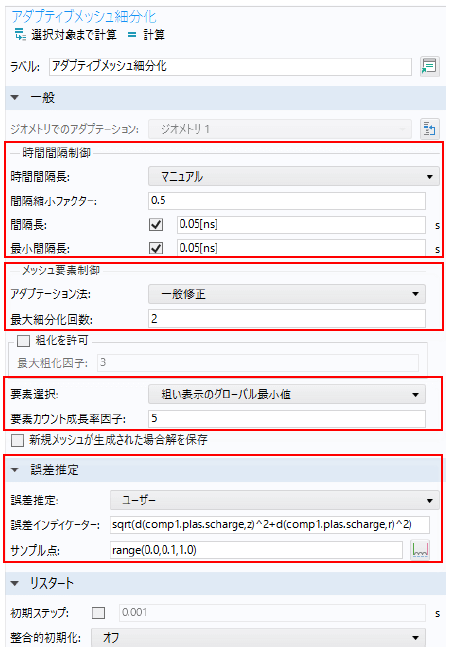
図1にCOMSOLのアダプティブメッシュ細分化の設定画面を示しており、設定方法は以下に纏められた。

1. 物理メカニズムを捉えるのに十分に細分化された初期メッシュを定義する。例：要素サイズ 50～70μm
2. 時間間隔長：0.05nsとする。ストリーマ速度は1×10⁶m/s、電荷分離層は50μmであれば、新しいメッシュを生成する時間間隔長は、50μm/1×10⁶m/s=0.05nsである。
3. アダプテーション法に「一般修正」、最大細分化回数に２とする。初期要素サイズは50μmであれば、細分化した後の要素サイズは、50μm/2/2=12.5μmになる。
4. 要素選択に「粗い表示のグローバル最小値」、要素カウント成長率因子に5とする。これによって、ストリーマの本体と横方向の空間電荷密度領域で適切な解像度を維持する。
5. 誤差推定に「ユーザー」、誤差インディケーターにsqrt(d(comp1.plas.scharge,z)^2+d(comp1.plas.scharge,r)^2)、サンプル点にrange(0.0,0.1,1.0)とする。変数plas.schargeは空間電荷密度である。

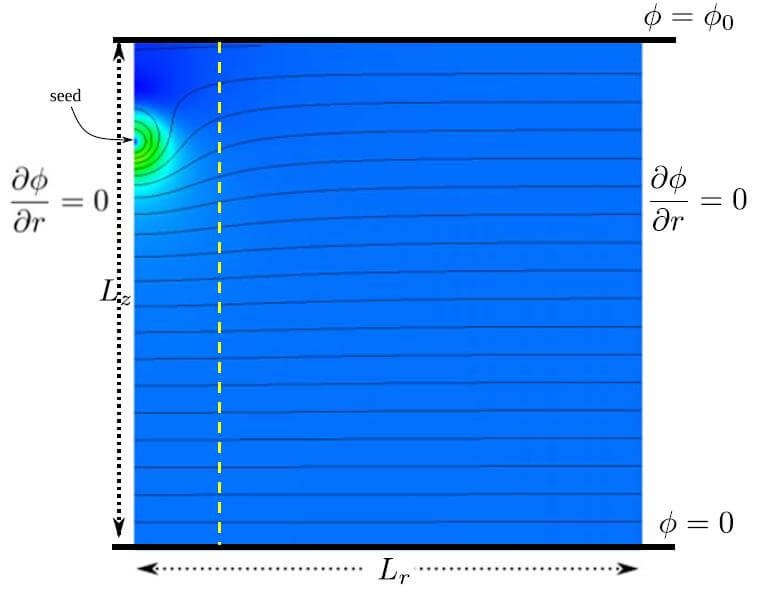
本例題は\(p=1 \rm bar\)と\(T=\rm 300K\)である80％N₂および20％O₂の乾燥した空気中のストリーマの放電を考慮する。モデル構造図を図2に示す。モデル領域は軸対称、\(L_r=L_z={\rm 1.25cm}, \phi_0=\rm 18.75kV\)である³⁾。

ガウス分布である正イオンのシードは式(2)で定義される。

\(\begin{align}
n_i(r,{\rm z})=N_0\exp\left [ -\frac{r^2+{\rm(z-z_0)^2}}{\sigma^2} \right ] \tag{2}
\end{align}\)

ここで、\(\rm N_0=5\times 10^{18}m^{-3},\sigma=0.4mm,z_0=1cm\)である。

本書ではモデルおよび、図4と図5の解析結果を作成する手順を示した。
計算モデルは、電子とイオンの輸送、空間電荷場の計算方程式を連立して計算を行うが、紙数の都合でここではこれらの方程式の説明を省略する。計算用の初期メッシュと一回目細分化したメッシュを図3に示す。初期メッシュの要素数は23542、細分化したメッシュの要素数は48231である。

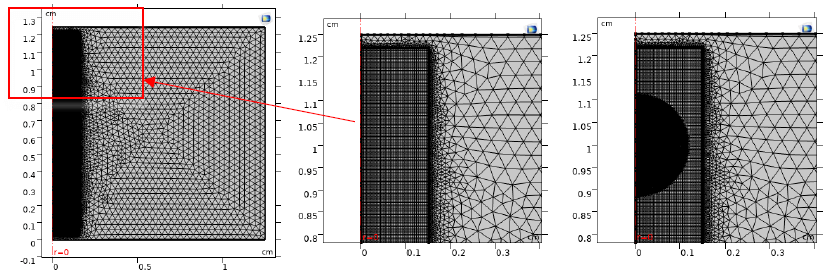
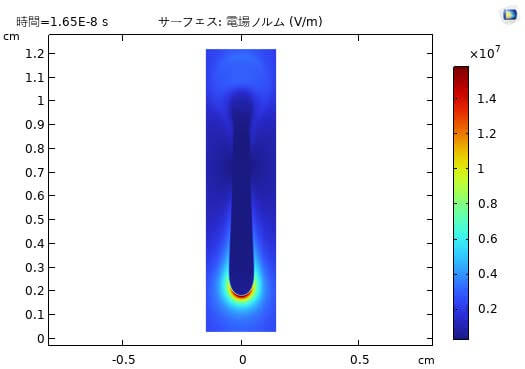
図4にストリーマ放電のシミュレーション結果、電界強度を示している。ガウス分布である正イオンのシードは電場を強化し、数ナノ秒以内に正ストリーマが下向きに発達する。16.5ns間のストリーマ 放電の成長過程を計算した。計算時間は27時間26分だった。

計算用のパソコンスペックは以下の通りであり、計算が11.86GBのメモリ(RAM)を利用した。

1. OS: WINDOWS10
2. CPU: Intel(R) Xeon(R) CPU E5-1660 v2 @3.70GHz
3. メモリ(RAM): 128GB

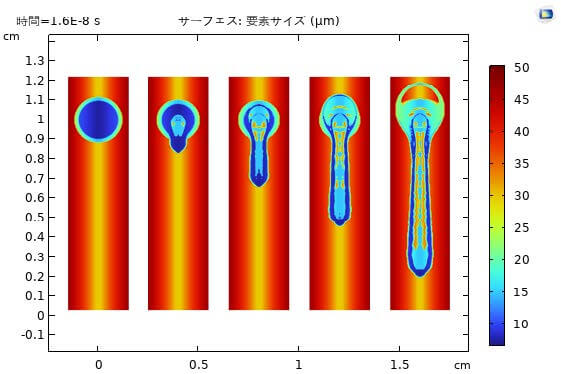
図5にアダプティブメッシュを示している。メッシュの要素サイズによって細分化効果を検証した。本例題は光電離モデルが含まれていない。代わりに、均一なバックグラウンドの電子とイオン電離密度、\(i.e.,10^{13}\rm m^{-3}\)が使用された³⁾。

参考文献

1) Y. V. Serdyuk, Propagation of Cathode-Directed Streamer Discharges in Air, Proceedings of 2013 COMSOL Conference in Rotterdam.
2) 佟 立柱, 低温プラズマシミュレーションのための適合格子細分化手法, 計算工学講演会論文集, Vol.24(2019年5月).
3) B. Bagheri, J. Teunissen, U. Ebert, et al., Comparison of Six Simulation Codes for Positive Streamers in Air, Plasma Sources Sci. Technol., 27, 095002 (2018).

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。