大気圧ストリーマ放電は化学反応性が高く、容易に発生させることが出来るといった特徴から、様々な技術応用が考えられている。ストリーマ放電に関する研究は主に絶縁破壊現象を解明する目的として古くから行われてきており、その理論はストリーマ理論として広く知られている。これらの技術をさらに発展および活用していくためには、ストリーマ放電の物理的、化学的な特徴を理解することは重要である。ストリーマ放電の基礎過程に関する研究は、実験とシミュレーションの両面から精力的に行われている。

ストリーマ放電は放電の進展速度が非常に速く、またその放電路は1mm以下の細いフィラメント構造を有することから、実験計測だけでは十分な時間分解能と空間分解能を得ることは難しい。このような状況において、ストリーマ放電シミュレーションを用いることは非常に有用である。ストリーマ放電シミュレーションでは、電子とイオンの集団を流体と近似したモデルを用いることが多い。加えて、流体モデルでは、荷電粒子の輸送パラメータが場の局所電界で瞬時に与えられると近似する局所電界近似法を併せて用いることが現状である¹⁾。

そこで本例題は、COMSOL Multiphysicsのプラズマモジュールに基づいて、 流体モデルに局所電界近似法を用い、移流拡散方程式とマクスウェル方程式を交互に解くことでストリーマの進展を再現する。COMSOLプラズマモジュール では、ストリーマ放電の計算方程式を以下に示している。

\begin{equation}
\begin{split}
&\frac{\partial n_e}{\partial_t}+\nabla・\Gamma_e=R_e-({\rm u}・\nabla)n_e \\
&\epsilon=F(E/N) \\
&{\rm \nabla・D}=\rho_q \\
&{\rm E}=-\nabla_V \\
&f(\epsilon)=\phi^{-3/2}\beta_1\exp\left (-(\epsilon\beta_2/\phi) \right ) \\
&\beta_1=\Gamma(5/2)^{(3/2)}\Gamma(3/2)^{(-5/2)} \\
&\beta_2=\Gamma(3/2)\Gamma(3/2)^{-1}
\end{split}
\end{equation}

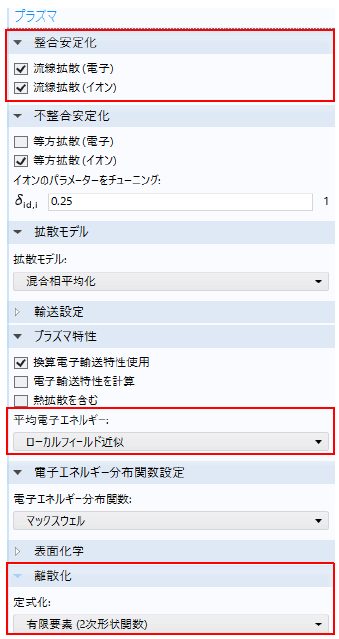
図1にCOMSOLのストリーマ放電の計算の設定画面を示す。ストリーマ計算においては電子およびイオン輸送方程式の流線拡散に基づく整合安定化が採用され、ストリーマ放電のペクレ数の高い系を求解することが可能になった。また、ローカルフィールド近似(局所電界近似法)を使用し、電子の平均エネルギー方程式は解かないため、計算が速くなった。

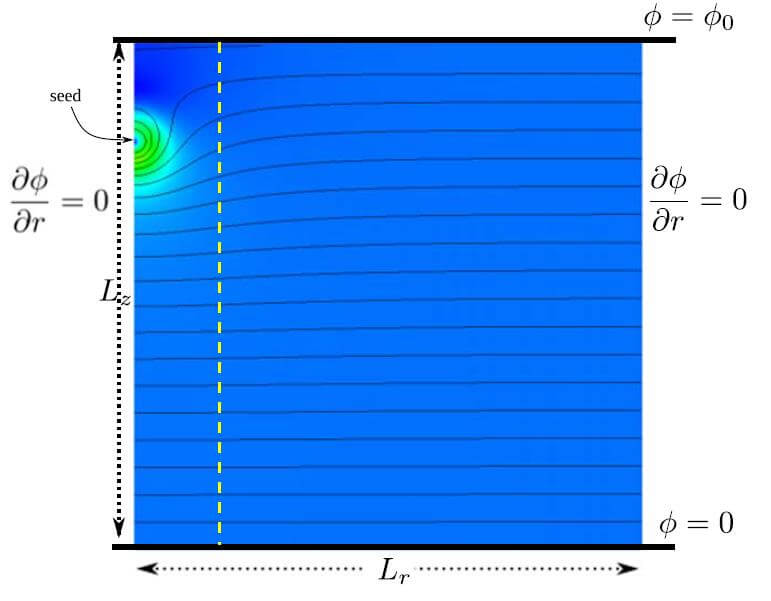
本例題は\(p=1{\rm bar}\)と\(T=300{\rm K}\)である80％N₂および20％O₂の乾燥した空気中のストリーマの放電を考慮する。モデル構造図を図2に示す。モデル領域は軸対称、\(L_r=L_z=1.25{\rm cm},\phi_0=18.75{\rm kV}\)である²⁾。ガウス分布である正イオンのシードは式(2)で定義される。

\(\begin{align}
n_i(r,{\rm z})=N_0\exp\left [ -\frac{r^2+{\rm(z-z_0)^2}}{\sigma^2} \right ] \tag{2}
\end{align}\)

ここで、\(\rm N_0=5\times 10^{18}m^{-3},\sigma=0.4mm,z_0=1cm\)である。

本書ではモデルおよび、図4の解析結果を作成する手順を示した。
計算モデルは、電子とイオンの輸送、空間電荷場の計算方程式を連立して計算を行うが、紙数の都合でここではこれらの方程式の説明を省略する。計算用の電子のドリフト速度と拡散係数および正味電離係数α’の絶対値は図3に示されている。

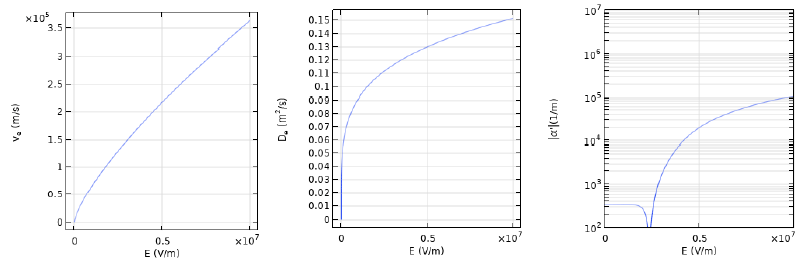
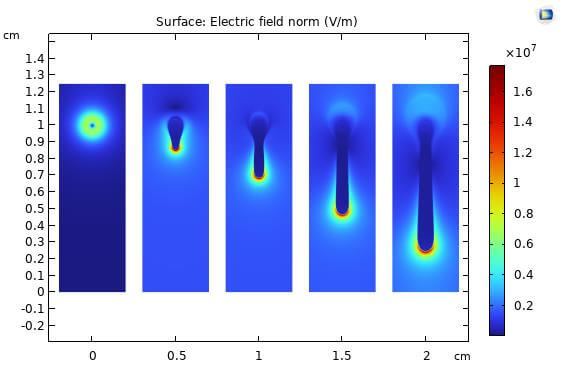
図4にストリーマ放電のシミュレーション結果、電界強度を示している。ガウス分布である正イオンのシードは電場を強化し、数ナノ秒以内に正ストリーマが下向きに発達する。計算では、20ns以内にストリーマが底部境界に到達した。計算時間は19時間40分だった。計算用のパソコンスペックは以下の通りであり、計算が12.07GBのメモリ(RAM)を利用した。

1. OS: WINDOWS 10
2. CPU: Intel(R) Xeon(R) CPU E5-1660 v2 @3.70GHz
3. メモリ(RAM): 128 GB

本例題は光電離モデルが含まれていない。代わりに、均一なバックグラウンドの電子とイオン電離密度、\(i.e.,10^{13}\rm m^{-3}\)が使用された²⁾。ストリーマ放電シミュレーションでは、高いバックグラウンド電子密度は頻繁に使われ、電子とイオンの密度勾配、さらにストリーマ先端の電場を減らすことで、計算上はストリーマ放電シミュレーションの実行が容易になる。

1) 小田昭紀，小室淳史，明石治朗，非平衡大気圧プラズマのシミュレーション，J. Plasma Fusion Res., Vol. 92, No.9, pp. 682-687 (2016).
2) B. Bagheri, J. Teunissen, U. Ebert, et al., Comparison of six simulation codes for positive streamers in air, Plasma Sources Sci. Technol., 27, 095002 (2018).

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。