乱流は、大小の渦(eddy) の非定常的な生成・消滅が生じる複雑な流れであるが、エンジニアリングにおいて興味があるのは、その平均的な挙動である。そのため、乱流の情報を得るために、乱流の支配方程式に対して平均化が施される。RANS乱流モデルは、この場合に導入されるものである。

RANSとは乱流モデルのひとつで、Reynolds-Averaged Navier-Stokesの頭文字をとったものである。RANSは流体の運動方程式であるナビエストークス方程式をアンサンブル平均して解く手法で、乱流の影響はすべて乱流モデルで表現する。RANSでは空間的・時間的に平均化を行うため、計算コストの削減が可能である。二次元、定常解析も可能なため、産業分野で一般的に活用されている。しかしながら、すべての流れ場において、実用的な解が得られるRANS 乱流モデルは存在しないため、流れ場に応じて適切なモデルを選択する必要がある¹⁾。

そこで本例題は、近年使用頻度が増加しているCOMSOL Multiphysicsの高レイノルズ数RANS乱流モデル：標準k-ε (2Eqn.)、低レイノルズ数RANS乱流モデル: 低Re k-ε (2Eqn.)、v²-f (3Eqn.)を対象に、室内噴流場を解析検証する。各の乱流モデルの特徴は以下にまとめられる。

a) 標準k-εモデル：収束性がよく産業界において最も広く使用されている。乱流エネルギーkと乱流散逸率を用いて渦粘性係数を計算する。標準k-εモデルは壁面に近い低レイノルズ数効果の大きい領域（粘性底層）を扱うことができない。強力な圧力勾配、剥離、強曲率流れを伴う複雑な流れには適さない。

b) 低Re k-εモデル：壁面近傍の低レイノルズ数効果の大きい粘性底層を扱えるよう修正を加えられたk-εモデルである。壁面の熱伝達係数を確認したい場合に適する。

c) v²-fモデル：拡張された低Re k-εモデルである。kとεに加えて壁の法線変動(v²)と楕円緩和関数(f)も計算する。曲面上の流れに対する優れた予測機能があり、熱伝達、表皮摩擦、および乱流境界層の分離を正確に予測できる。

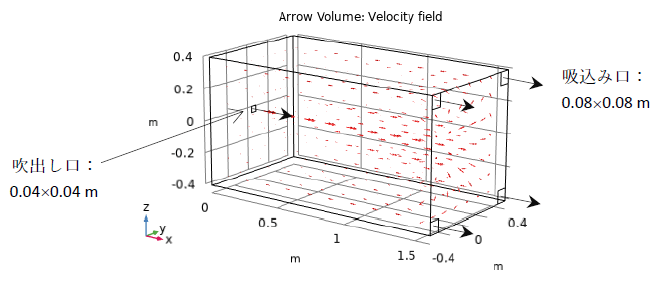
解析モデルは図１に示す。三次元モデルであり、後藤ら¹⁾により模型実験が行われた吹出し口Reが比較的小さい噴流場を検討する。噴流場の長さは1.6m、吹出し口の大きさは0.04×0.04m、4ケ所の吸込み口の大きさは0.08×0.08mである。空気の温度は20℃、圧力は1atmである。

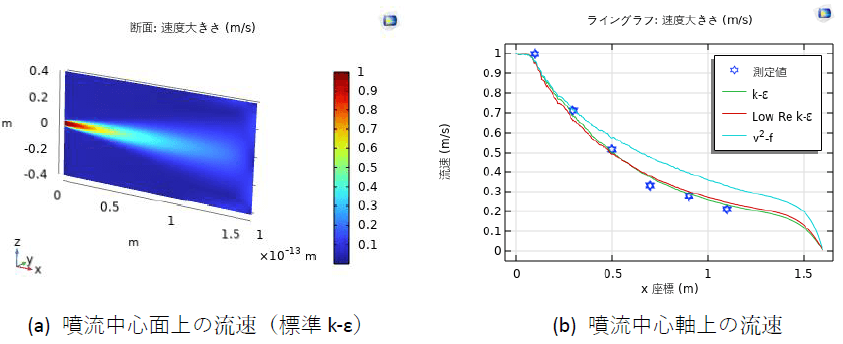
本書ではモデルおよび、図2の解析結果を作成する手順を示した。

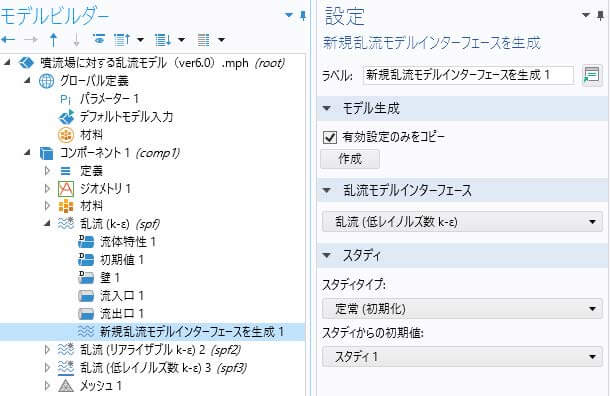
計算には、流入口に流速1m/s、流出口に圧力1atmを設定し、まず、標準k-ε乱流モデルを用いて室内噴流場を解きます。次に、標準k-ε乱流モデルによる計算結果に基づいてCOMSOL「新規乱流モデルインターフェースを生成」ノードを用いて、他の乱流モデルを作成し計算を行う。

k-ε乱流モデルの支配方程式は次の式で示される。

\(\begin{align}
& \rho({\bf u}・\nabla){\bf u}=\nabla・{\bf[-\rho l+K]+F} \\
& \nabla・(\rho{\bf u})=0\\
& {\bf K}=(\mu+\mu_{\rm T})(\nabla{\bf u}+(\nabla{\bf u})^{\rm T})-\frac23(\mu+\mu_{\rm T})(\nabla・{\bf u}){\bf l}-\frac23\rho k{\bf l}\\
& \rho({\bf u}・\nabla)k=\nabla・\left[\left(\mu+\frac{\mu_{\rm T}}{\sigma_{\rm k}}\right)\nabla_k\right]+P_{\rm k}-\rho\epsilon\\
& \rho({\bf u}・\nabla)k=\nabla・\left[\left(\mu+\frac{\mu_{\rm T}}{\sigma_{\epsilon}}\right)\nabla_\epsilon\right]+C_{\epsilon 1}\frac{\epsilon}{k}P_{\rm k}-C_{\epsilon 2}\frac{\epsilon^2}{k},~\epsilon={\rm ep}\\
\\
& \mu_{\rm T} =\rho c_\mu\frac{k^2}{\epsilon}\\
& P_{\rm k}=\mu_{\rm T} \left[\nabla{\bf u}：(\nabla{\bf u}+(\nabla{\bf u})^{\rm T})-\frac23(\nabla・{\bf u})^2 \right]-\frac23\rho k\nabla・{\bf u} \tag{1}
\end{align}\)

紙数の都合でここではこれらの方程式および他の乱流モデルの説明を省略する。

図2(a)に標準k-ε乱流モデルによる計算結果、室内噴流場における噴流中心面上の流速を示している。各の乱流モデルによる噴流中心軸上の流速を測定値¹⁾と比較した結果は図2(b)に示される。標準k-εモデルと低Re k-εモデルは測定値と一致することが分かった。v²-fモデルでは、既往の報告で、伝熱・冷却問題に対して有効なモデルとされている²⁾が、本例題の室内噴流場に対して、噴流の発達領域の予測精度が低下した。

参考文献

1) 後藤和恭, 酒井孝司, 小野浩己，等温噴流場におけるRANS乱流モデルの予測精度の検証，空気調和・衛生工学会論文集, Vol. 43, No. 257, pp. 1-9 (2018).
2) 船崎健一，ガスタービンの冷却問題におけるCFD解析，日本ガスタービン学会誌，Vol. 32, No. 4, pp. 270-277 (2004).

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。