流体機械内部で発生する剥離流れは大規模な再循環領域を形成し、圧力損失やサージングといった非定常現象を引き起こし、流体機械の駆動効率を低下させる。近年、小型流体機械の開発が注目され、低レイノルズ数域における剥離再付着流れおよび流動機構は製品性能に大きく影響するため流れ構造の理解が重要である¹⁾。

後方ステップ流れでは、再循環領域の大きさを再付着距離で評価できることから、制御ディバイスの評価に有効であると考えられる。図1に血液検査や尿検査を可能とするマイクロ流体プラットフォーム装置は示される²⁾。

計測測定により壁面近傍の流れや横渦の周波数特性、剥離せん断層の特性を理解することができるが、実験、試作にはコストがかかるため、流体解析が活用されている。流体解析は模擬実験や理論の確認、理解などに有意義であり、可視化、共有も行える。そこで本例題はCOMSOL Multiphysicsのk-ε乱流モデルを用いて、低レイノルズ数域における後方ステップ流れ計算およびアダプティブメッシュ（適合格子細分化法）の適用性の検討を行う。

k-ε乱流モデルの支配方程式は次の式で示される。

\(\begin{align}
& \rho({\bf u}・\nabla){\bf u}=\nabla・{\bf[-\rho l+K]+F} \\
& \nabla・(\rho{\bf u})=0\\
& {\bf K}=(\mu+\mu_{\rm T})(\nabla{\bf u}+(\nabla{\bf u})^{\rm T})-\frac23(\mu+\mu_{\rm T})(\nabla・{\bf u}){\bf l}-\frac23\rho k{\bf l}\\
& \rho({\bf u}・\nabla)k=\nabla・\left[\left(\mu+\frac{\mu_{\rm T}}{\sigma_{\rm k}}\right)\nabla_k\right]+P_{\rm k}-\rho\epsilon\\
& \rho({\bf u}・\nabla)k=\nabla・\left[\left(\mu+\frac{\mu_{\rm T}}{\sigma_{\epsilon}}\right)\nabla_\epsilon\right]+C_{\epsilon 1}\frac{\epsilon}{k}P_{\rm k}-C_{\epsilon 2}\frac{\epsilon^2}{k},~\epsilon={\rm ep}\\
\\
& \mu_{\rm T} =\rho c_\mu\frac{k^2}{\epsilon}\\
& P_{\rm k}=\mu_{\rm T} \left[\nabla{\bf u}：(\nabla{\bf u}+(\nabla{\bf u})^{\rm T})-\frac23(\nabla・{\bf u})^2 \right]-\frac23\rho k\nabla・{\bf u} \tag{1}
\end{align}\)

紙数の都合でここではこれらの方程式の説明を省略する。

アダプティブメッシュとは、解析結果に基づいてメッシュを細分化する手法である。アダプティブメッシュは最初に初期メッシュで解析し、エラーが高いと推定される領域に繰り返し要素を挿入し、モデルを再解決する。これは、必要に応じて何回でも繰り返すことである。本例題のアダプティブメッシュの解析手順は以下に示される。

1. 定常ソルバーを使用して、初期メッシュにて解析
2. 偏微分方程式の残差を評価
3. 「誤差のL2ノルム二乗」という手法によって解の誤差を推定
4. 推定誤差に応じて要素を細分化する。
5. 指定した細分化回数を超えるまで、この手順を繰り返す。

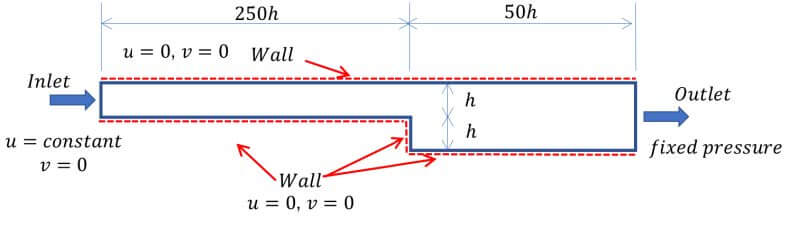
解析モデル³⁾は図2に示す。2Dモデルであり、流れの温度変化が小さいため、流れは非圧縮性であると見なせる。低レイノルズ数域（Re=100~800）後方ステップ流れの計算を行う。

本書ではモデルおよび、図3の解析結果を作成する手順を示した。

計算には、入口流速と高さはそれぞれu=Re×ν/h、h=1cmで定義される。ここでνは動粘性係数である。アダプティブメッシュは、L2ノルム誤差推定手法を使用し、細分化する格子の割合が式(2)で計算される。

\(\begin{align}
\left(\smallint_\Omega\Sigma_l S_l^{-2}h^{2ql}\lvert\rho_l\lvert^2dA\right)^{\frac12} \tag{2}
\end{align}\)

ここで、\(\rho_l\)は方程式\(l\)の残差、\(q_l\)は安定性評価微分次数、\(S_l\)はスケーリング因子、\(h\)はメッシュ要素サイズ、\(A\)はメッシュ要素の面積である。

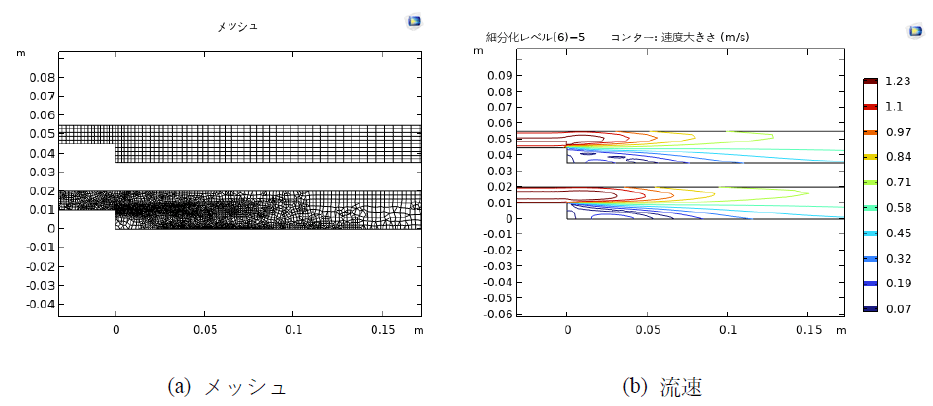
図3に低レイノルズ数域における後方ステップ流れの計算結果を示している。レイノルズ数Re=800であり、流路の左から流れが領域に入ってくると流れは段差に到達すると剥離することが再現された。上図はスタンダードメッシュ（マップトメッシュ）³⁾、下図は5回アダプティブメッシュを作成した。計算結果はメッシュの品質に依存していると示された。

参考文献

1) 山田俊輔, 本阿弥眞治, 岡本圭太, 新田貴志, 元祐昌廣, 石川仁, “低レイノルズ数域における後方ステップ流れの制御に関する研究（安定性解析を利用したSynthetic jetによる再付着流れの制御）”, 日本機械学会論文集B 編, Vol. 77, No. 775 (2011), pp. 279-287．
2) OISTニュース, https://www.oist.jp/ja/node/28444.
3) Li, Z.Q. and Li, M., “Accuracy verification of a 2D adaptive mesh refinement method using backward-facing step flow of low Reynolds numbers”, International Journal of Computational Methods, Vol. 18, No. 3 (2021), p. 2041012.

＊該当のCOMSOLモデルファイルと手順書をご要望のお客様は下記よりダウンロードいただけます。