腐食におけるアノード溶解による金属表面形状が大きく変化することがある。形状変化の計算手法は腐食の数値解析モデルの構成要素の１つであり、固定メッシュを用いて金属表面を間接的に表現する方法（界面捕捉法）と移動メッシュを用いて金属表面を直接的に表現する方法（界面追跡法）に大別される。代表的な形状変化の計算手法はEuler手法でのVOF（volume-of-fluid）法、レベルセット法、フェーズフィールド法およびLagrange法とEuler法が混合されたALE（arbitrary Lagrangian-Eulerian）法などが挙げられる。レベルセット法では、複雑な形状を表現することが可能であり、さらに、レベルセット関数を更新することにより、形状変化のみならず、形態変化も自然に表現できるため、流体力学など幅広い範囲に応用されている。

この計算例は、レベルセット法による腐食の数値解析のモデリングを行う。局部腐食進展挙動を解析し、ALE 法による計算結果および試験結果と比較することで計算効率を考察する。

本書では解析および、図2の解析結果を作成する手順を示した。

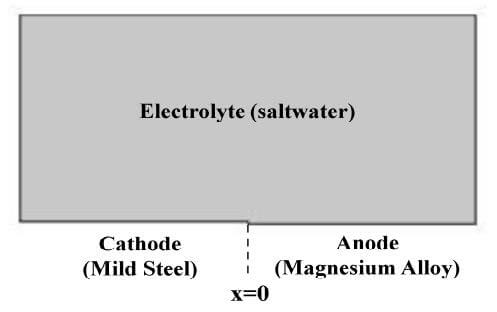
計算ジオメトリは、図1に示すような、軟鋼とマグネシウム合金(AE44)のガルバニック腐食解析モデルである。マグネシウム合金の酸化反応は以下のように考慮される。

\(\rm Mg(s)\Rightarrow Mg^{2+}(aq)+2{\mathit e^-}\)

拡散制限アノードターフェル式は以下のように示される。

\(i_{\rm tafel}=i_{\rm 0,an}・10^{\eta / A_{an}},~i_{\rm an}=\frac{i_{\rm lim}}{1+\frac{i_{\rm lim}}{i_{\rm tafel}}}\)

ここで、\(i_{\rm 0,an}\)は分極特性の交換電流密度、\(\eta\)は過電圧、\(A_{an}\)はターフェル勾配、\(i_{\rm lim}\)は限界電流密度である。マグネシウム合金の酸化反応によって、金属の境界が金属内の法線方向に移動し腐食速度は次式で算出される。

\(\nu_{\rm corr}=\frac{i_{\rm an}}{2F}\frac M\rho\)

ここで、\(F\)はファラデー定数、\(M\)はモル質量、\(\rho\)は密度である。

カソード表⾯の化学反応は、カソードターフェル式に従い、

\(i_{\rm cat}=-i_{\rm 0,cat}・10^{\eta/A_{cat}}\)

レベルセット法による腐食計算は以下のレベルセット関数の計算方程式を解く。

\(\frac{\partial \phi}{\partial t}+{\bf u}・\nabla\phi=\gamma\nabla・(\epsilon\nabla\phi-\phi(1-\phi)\frac{\nabla\phi}{|\nabla\phi|})\)

ここで、\(\bf u\)は金属表面の移動速度である。\(\phi\)はレベルセット関数であり、次式で定義される。

\(\phi(x,y,t)= \left[
\begin{array}{lll}
<0.5 ~ \text{電解質} \\
=0.5 ~ \text{界面} \\
>0.5 ~ \text{金属} \\
\end{array}
\right. \)

界面は\(\phi=0.5\)で表される。\(\epsilon\)は界面の厚さ、\(\gamma\)は界面の再初期化パラメータである。ここでは、\(\gamma=\nu_{\rm corr}\)とする。

レベルセット関数\(\phi\)を用いたデルタ関数は以下のように表される。

\(\delta=6|\phi(1-\phi)||\nabla\phi|\)

レベルセット法による腐食計算は電極を微小な電解質導電率がある電解質と定義し、次式で全領域の電解質導電率を求める。

\(\sigma=\sigma_{\rm ed}\times{\rm Vf2}+\sigma_{\rm el}\times{\rm Vf1}\)

ここで、\(\sigma_{\rm el}\)と\(\sigma_{\rm ed}\)はそれぞれ電解質・電極中の電解質導電率、Vf1とVf2はそれぞれ電解質・電極の体積比率を意味する。金属表面の化学反応は、以下のように電解質電流ソース\(Q_l\)で計算される。

\(Q_l=i_{\rm an}\delta\)

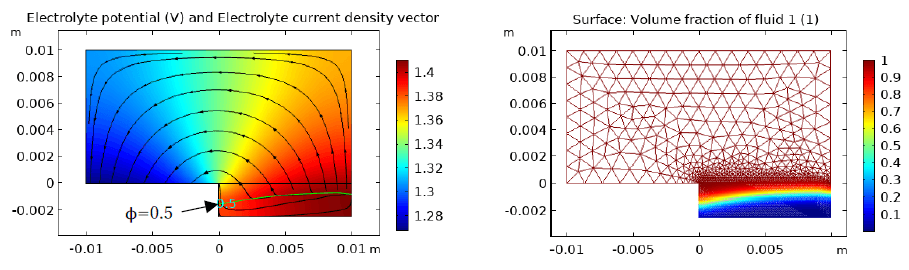
図2に腐食により3日後の電解質電位・電流密度、金属表面形状および電解質の体積比率を示している。固定メッシュに基づくレベルセット法により複雑な金属表面形状を捕捉することは可能になったが、腐食する金属領域にはかなり細かいメッシュを作成する必要になることが分かった。

参考文献

1) 佟立柱, 永山達彦, 汎用シミュレーションソフトによる腐食解析, 計算工学, Vol.25, No.3, 4099-4104 (2020).
2) 佟立柱, 腐食防食の高度な数値解析ツールCOMSOL Multiphysics, 材料と環境, Vol.62，No.10, 372-376

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。