CASES AND MATERIALS
事例/資料
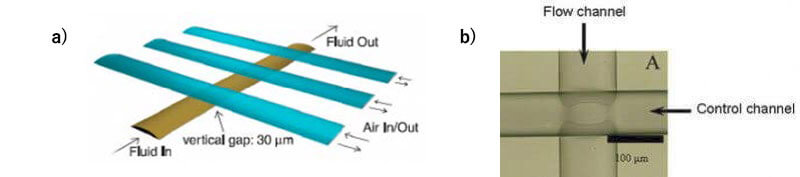
生体模倣システム (microphysiological system:MPS) ${ }^{1,2)}$ とは、 MEMS (micro electro mechanical systems)技術を用いて作製された微小な空間に、生体(in vivo)に近い培養環境を再構築したin vitro培養系のことである。マイクロ流体デバイスを細胞培養に利用する場合、生体内を模倣した微細構造を人工的に作製できること、液性条件や接着条件を時間的・空間的に制御できること、せん断応力や伸縮などの物理刺激を負荷できることなど、従来の細胞培養系では再現することが困難な培養環境を構築することができる。 Quake型バルブ3は、多層ソフトリソグラフィーから開発されたもので、3セットのマイクロバルブで閉弁と中圧送液を実現することができ、広く使 用されている(図 1 (a)). 図1(b)に2層構造Quake型バルブを示す。ポリジメチルシロキサン (PDMS) ダイアフラムの変形と半円形のチャネルの結合で構築された。
体積弾性率 $\kappa(\mathrm{Pa}): \quad E /[3 \times(1-2 \times v)]$
ラメ定数 $\mu\left(\mathrm{N} / \mathrm{m}^{2}\right): \quad E /[2 \times(1+v)]$
材料の密度 $\rho\left(\mathrm{kg} / \mathrm{m}^{3}\right): 920$
本書では、モデルおよび、2 章以後に図 3 と図 4 の解析結果を作成する手順を示す。
図 3 に $65 \mathrm{kPa}$ 圧力での PDMS 膜の変形した $3 \mathrm{D}$ プロファイルを示している。COMSOL パラメト リックスイープ機能によって、ダイアフラムの空気圧力層から 0 65 kPa の圧力を設定する。我々は、シミュレーション結果に基づいて、最適化されたグレースケールリソグラフィプロセスに よって図 4 に示した高さ $45 \mu \mathrm{m}$ の半円流路と $200 \mu \mathrm{m} \times 200 \mu \mathrm{m}$ の膜表面積を持つマイクロバルブ デバイスを製造した。
製造されたマイクロバルブのフォトレジスト金型プロファイルは、触針式プロファイラ (DektakXT-S、Bruker)によって測定された。測定結果と $65 \mathrm{kPa}$ の圧力でのシミュレーション膜 変形プロファイルの比較は図 5 に示されている。両者は概ね一致したことは検証された。測定值 とシミュレーション結果の間の小さい誤差は、プロセス条件によって PDMS の材料特性を変化 させた結果であると考えられる。PDMS のヤング率は、 $50 \mathrm{kPa}$ から $4 \mathrm{MPa}$ まで変化される試験が 既に報告された ${ }^{5)}$.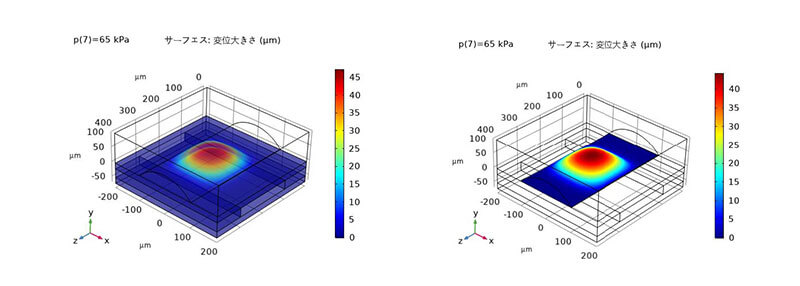
2) R. Gómez-Sjöberg, A.A. Leyrat, D.M. Pirone, C.S. Chen and S.R. Quake, Anal. Chem., 79 (2007) 85578563.
3) M.A. Unger, H.P. Chou, T. Thorsen, A. Scherer and S.R. Quake, Science, 288 (2000) 113-116.
4) K. Kamei, Y. Kato, Y. Hirai, S. Ito, J. Satoh, A. Oka, T. Tsuchiya, Y. Chen, O. Tabata, RSC Adv., 7 (2017) 36777.
5) I.D. Johnston, D.K. McCluskey, C.K.L. Tan and M.C. Tracey, J. Micromech. Microeng., 24 (2014) 35017.

図 1. Quake 型マイクロバルブ.
デジタルグレースケールマスクパターンの設計はQuake 型バルブを構築する重要なステップ である。これには半円形のチャネルの断面が有限要素解析(FEA)シミュレーションで得られた PDMS のダイアフラム変形と同様に作製することが有効である ${ }^{4)}$ 。そこで本例題はマイクロバ ルブの設計最適化を達成するために、COMSOL MultiphysicsのNeo-Hookean 超弾性材料モデルを用いて正方形のポリジメチルシロキサン(PDMS) 膜変形の計算を行った。Neo-Hookean 超弾性材 料モデルは次の式で示される。 $$ \begin{aligned} & 0=\nabla \cdot(\mathrm{FS})^{\top}+\mathrm{Fv}, \quad \mathrm{F}=1+\nabla \mathbf{u} \\ & \mathrm{S}=\mathrm{S}_{\text {inel }}+\frac{\partial W_{\mathrm{s}}}{\partial \epsilon}, \quad \sigma=J^{-1} \mathrm{FSF}^{\top}, \quad J=\operatorname{det}(\mathrm{F}) \\ & \epsilon=\frac{1}{2}\left(\mathrm{~F}^{\top} \mathrm{F}-1\right) \\ & W_{\mathrm{s}}=\frac{1}{2} \mu\left(\bar{l}_{1}-3\right)+\frac{1}{2} K\left(J_{\mathrm{el}}-1\right)^{2} \end{aligned} $$ 半円流路への膜変形の接触解析をPenalty法によって次の式を解く。 $$ \begin{aligned} & T_{\mathrm{n}}=\text { if }\left(g_{\mathrm{n}} \leq 0,-p_{\mathrm{n}} g_{\mathrm{n}}, 0\right) \\ & p_{\mathrm{n}}=f_{\mathrm{p}} \frac{E_{\text {char. }}}{h_{\text {min }}} \end{aligned} $$ 紙数の都合でここではこれらの方程式の説明を省略する。
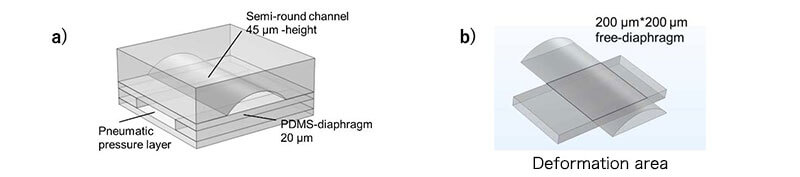
図 2. 解析モデル.
解析モデルは図 2 に示す。3D モデルであり、 $80^{\circ} \mathrm{C}$ の PDMS 硬化プロセス条件下での $1.89 \mathrm{MPa}$ のヤング率 $(E)$ と 0.499 のポアソン比 $(v)^{5)}$ が採用された。計算のパラメーターは以下の通りに定 義される。体積弾性率 $\kappa(\mathrm{Pa}): \quad E /[3 \times(1-2 \times v)]$
ラメ定数 $\mu\left(\mathrm{N} / \mathrm{m}^{2}\right): \quad E /[2 \times(1+v)]$
材料の密度 $\rho\left(\mathrm{kg} / \mathrm{m}^{3}\right): 920$
本書では、モデルおよび、2 章以後に図 3 と図 4 の解析結果を作成する手順を示す。
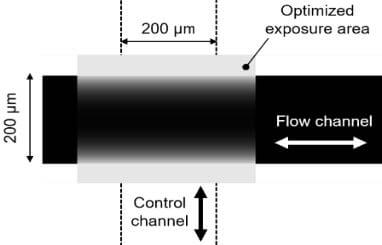
図 3 に $65 \mathrm{kPa}$ 圧力での PDMS 膜の変形した $3 \mathrm{D}$ プロファイルを示している。COMSOL パラメト リックスイープ機能によって、ダイアフラムの空気圧力層から 0 65 kPa の圧力を設定する。我々は、シミュレーション結果に基づいて、最適化されたグレースケールリソグラフィプロセスに よって図 4 に示した高さ $45 \mu \mathrm{m}$ の半円流路と $200 \mu \mathrm{m} \times 200 \mu \mathrm{m}$ の膜表面積を持つマイクロバルブ デバイスを製造した。
製造されたマイクロバルブのフォトレジスト金型プロファイルは、触針式プロファイラ (DektakXT-S、Bruker)によって測定された。測定結果と $65 \mathrm{kPa}$ の圧力でのシミュレーション膜 変形プロファイルの比較は図 5 に示されている。両者は概ね一致したことは検証された。測定值 とシミュレーション結果の間の小さい誤差は、プロセス条件によって PDMS の材料特性を変化 させた結果であると考えられる。PDMS のヤング率は、 $50 \mathrm{kPa}$ から $4 \mathrm{MPa}$ まで変化される試験が 既に報告された ${ }^{5)}$.

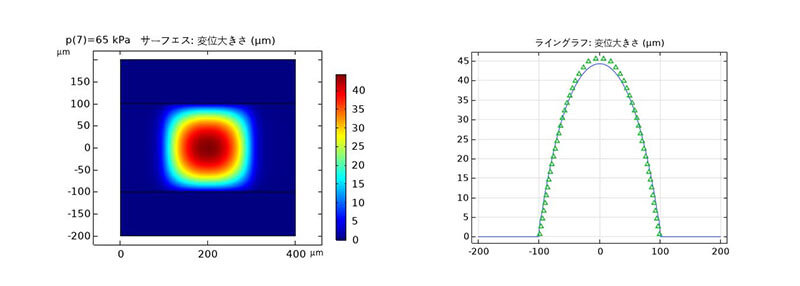
図 $3.65 \mathrm{kPa}$ 圧力でのPDMS 膜変形の3Dプロファイル.

図 4. マイクロバルブを作り出す最適化されたグレースケールパターン.

図 5. ダイアフラムの 表面変位および 測定した 金型プロファイル (△)との比較.
参考文献
1) H. Azizgolshani, J.R. Coppeta, E. M. Vedula, et al., Lab Chip, 21 (2021) 1454-1474.2) R. Gómez-Sjöberg, A.A. Leyrat, D.M. Pirone, C.S. Chen and S.R. Quake, Anal. Chem., 79 (2007) 85578563.
3) M.A. Unger, H.P. Chou, T. Thorsen, A. Scherer and S.R. Quake, Science, 288 (2000) 113-116.
4) K. Kamei, Y. Kato, Y. Hirai, S. Ito, J. Satoh, A. Oka, T. Tsuchiya, Y. Chen, O. Tabata, RSC Adv., 7 (2017) 36777.
5) I.D. Johnston, D.K. McCluskey, C.K.L. Tan and M.C. Tracey, J. Micromech. Microeng., 24 (2014) 35017.
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。