CASES AND MATERIALS
事例/資料
電気化学過程の解析は大学学部レベルの物理化学教科書に現れる、熱力学と反応論に基づいた電気化学の基本的な内容に加え、支持電解質の役割、電気二重層の形成、溶液内の電位分布、参照電極と三電極法、などの理解が必要になっているが、シミュレーションではプログラミング上の技巧が煩雑で、現実の電気化学系を処理するには多大な労力を要する。ここでは、電気化学過程における溶液内での拡散過程を重要な役割として、有限要素法の汎用ソフトウェアCOMSOL Multiphysicsを用いて計算した。電極反応による電気化学系における濃度変化のシミュレーション手法を紹介し、電気化学を学んでゆこうとする初心者への手引きとなると考えられる。
本例題は、長さ $L$ の 1 次元系で、左端 $(x=0)$ が電極、右端 $(x=L)$ がバルクに接した系を考える。電極での反応として、不可逆の酸化反応
$$
\mathrm{Red} \rightarrow \mathrm{Ox}+n \mathrm{e}^{-} (1)
$$
だけが起こり、生成した酸化型は電気化学的に不活性か、あるいは速やかに電気化学不活性な物質に変化するとする。
最初、過電圧が負の大きな值をとり、系全体がバルク濃度の還元体で占められている状態にあって、その状態が維持されているとする。そこに時刻 $t=0$ から $t=t_{d}$ の間、正の一定の過電圧 $\eta=$ $E-E_{0}>0$ を加えた場合の系の電流の時間変化を観測、即ち電位ステップクロノアンペロメトリー (PSCA)の実験を行なう。過電圧 $\eta$ の下での電極反応速度は、式(1)が不可逆反応なので、その反応速度は Buttler-Volmer 式1) $$ k_{0}^{+} \cdot C_{\mathrm{R}} \cdot \exp \left(\frac{\alpha n F}{R T}\left(E-E_{0}\right)\right)-k_{0}^{-} \cdot C_{0} \cdot \exp \left(-\frac{(1-\alpha) n F}{R T}\left(E-E_{0}\right)\right) (2) $$ の酸化項のみ(Anode Tafel 式)によって、$k_{0}^{+} を k_{0}$ に書き換え、 $$ k_{0} \cdot C_{\mathrm{R}} \cdot \exp \left(\frac{\alpha \eta F}{R T}\left(E-E_{0}\right)\right)=k_{0} \cdot C_{\mathrm{R}} \cdot \exp (\eta / A) (3) $$ と表せる。ここでRは気体定数、$T$ は熱力学温度、$C_{\mathrm{R}}$ は電極界面での還元体の濃度、$A=\frac{R T}{\alpha n F}$ である。ここで速度定数 $k_{0}$ は参照交換電流密度 $i_{0, \mathrm{ref}}$ との間にファラデー定数 $F を$ 用い、 $$ i_{0, \text { ref }}=n F k_{0} (4) $$ の関係がある。酸化体は上述のように系の電気化学に関係しないので、系の濃度としては還元体の濃度だけを考えれば良い。 本例題は、COMSOL Multiphysics の電気化学モジュールを利用し、次の Anode Tafel 式 $$ i_{\mathrm{loc}}=i_{0} \times 10^{\eta / \mathrm{A}_{a}} (5) $$ になった。 $i_{0}$ は交換電流密度、$i_{0}=i_{0, \mathrm{ref}} \cdot C_{\mathrm{R}}, \mathrm{A}_{a}=2.303 \times \mathrm{A}$ である。
($𝑥=exp (𝜂/𝐴)$であれば, $𝜂/𝐴=ln(𝑥)=2.303log (𝑥)$になり,そして, $𝑥= 10^{\eta / \mathrm{(2.303×A)}}$ であった。)
計算は、1 次元モデルを用いて行った。セルの長さ $\mathrm{L}=0.1 \mathrm{~cm}$, 還元体のバルク濃度 $c_{\text {bulk }}=1$ $\mathrm{mmol} / \mathrm{L}$, 拡散係数 $\mathrm{D}=1 \times 10^{-9} \mathrm{~m}^{2} / \mathrm{s}$, 熱力学温度 $\mathrm{T}=298.15 \mathrm{~K}$, 系の持続時間 $\mathrm{td}=100 \mathrm{~s}$, 電極界面 の反応速度定数 $\mathrm{k}_{0}=1 \times 10^{-6} \mathrm{~cm} / \mathrm{s}$, 初期電極電位 $\mathrm{E}_{0}=-1 \mathrm{~V}$, 印加電極電位 $\mathrm{E}_{1} は 0.3 \mathrm{~V}$, とした。
本書では、解析モデルおよび、2章以後に図 1 4 の解析結果を作成する手順を示す。 濃度分布の時間変化を図 1 に示す。 $t=0 \mathrm{~s}$ では全領域がバルク濃度であったが、時間経過とともに左端の電極から濃度が減少し、それが拡散によって右側の領域に広がっていく様子が見てとれる。右端は境界条件によりバルク濃度に固定されている。 領域を 5 等分した各点と両端の濃度の時間変化を図 2 に示す。右端では濃度はバルク濃度で一定であるが、電極に近づくにつれて、ある時刻から濃度の減少が始まることが分る。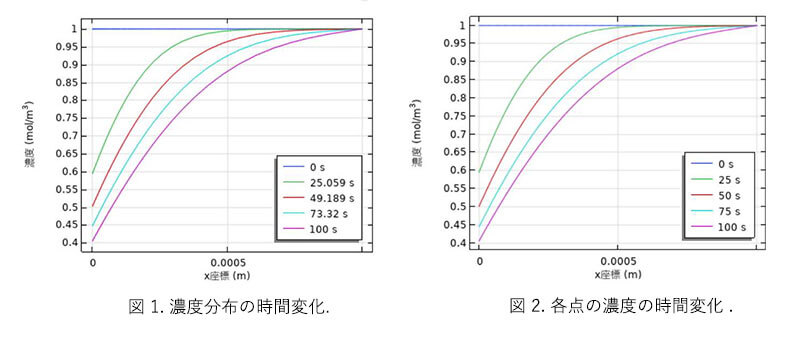
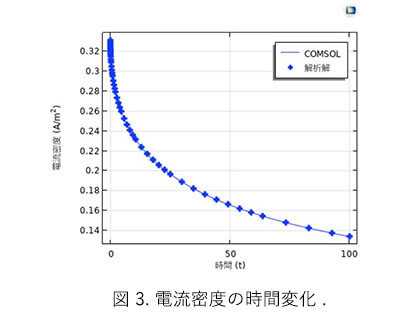
電流密度の時間変化を図 3 に示す,最初は大きな電流が流れ,それが時間とともに減衰していく。 図 1 から読み取った $100 \mathrm{~s}$ 経過後の左端電極付近の濃度勾配はおよそ $1.3 \times 10^{3} \mathrm{~mol} / \mathrm{m}^{4}$ なので、
これと拡散係数 $10^{-9} \mathrm{~m}^{2} / \mathrm{s}$ の積 即ち $1.3 \times 10^{-6} \mathrm{~mol} /\left(\mathrm{s} \mathrm{m}^{2}\right)$ が電極付近に単位面積、単位時間当たり拡散によって流れ込む還元体の物質量となる。そしてこれが電極反応で単位面積単位時間当たり消失する還元体の物質量と釣り合っているので、$n(=1)$ とファラデー定数とを掛けると,電極電流がおよそ $0.13 \mathrm{~A} / \mathrm{m}^{2}$ と求められる。これは図 3 から読み取った $100 \mathrm{~s}$ 経過後の電流密度の值とよく一致している。 図 3 には解析解も示されている。 解析解は次式の上うに与えられている ${ }^{2,3)}$. $$ i=n F k C \exp \left(\frac{k^{2} t}{D}\right) \times \operatorname{erfc}\left(k \sqrt{\frac{t}{D}}\right) (6) $$ 但し, $$ k=k_{0} \cdot \exp \left(\frac{\alpha n F}{R T}\left(E-E_{0}\right)\right) (7) $$ と置いた。また $C$ は還元体の初期濃度、erfc は余誤差関数である。 実際の計算に当たって、式(7)の指数関数部分がオーバーフローする場合には、余誤差関数の漸近展開 ${ }^{4,5)}$ $$ \operatorname{erfc}(x) \approx \frac{e^{-x^{2}}}{\sqrt{\pi}}\left(\frac{1}{x}-\frac{1}{2 x^{3}}+\frac{3}{4 x^{5}}-\frac{15}{8 x^{7}}+\cdots\right) (8) $$ を用いて、$x=k \sqrt{\frac{t}{D}}>15$ に対しては、$\frac{15}{8 x^{6}}<1.646 \times 10^{-7}$ が成立するので, $$ \operatorname{erfc}\left(x^{2}\right) \operatorname{erfc}(x) \approx \frac{1}{x \sqrt{\pi}}\left(1-\frac{1}{2 x^{2}}+\frac{3}{4 x^{4}}-\cdots\right) (9) $$ が 6 桁目までは正しい值を与える。このとき式(6)は $$ i \approx n F C \sqrt{\frac{D}{\pi t}}\left(1-\frac{1}{2 x^{2}}+\frac{3}{4 x^{4}}\right) (10) $$
となる。式(10)により、$𝑥→∞$の極限では式(6)が Cottrell式$i=n F C \sqrt{\frac{D}{\pi t}}$になることを理解できる。
電極電位 $\mathrm{E}_{1}$ を $0.2 \mathrm{~V}$ から $0.6 \mathrm{~V}$ まで $0.1 \mathrm{~V}$ 刻みに変元て電流密度の時間変化を見たものは図 4 で ある。 電極電位を上げていくと、式(3)に従って電極反応速度が大きくなり電流密度も増大するが、0.5 $\mathrm{V}$ と $0.6 \mathrm{~V}$ が殆ど重なっていることから、ある一定值に収束していくことが分る。この収束先は、電極の付近の濃度が一瞬にしてゼロとなったとして拡散方程式を解くと得られる Cottrell の式である。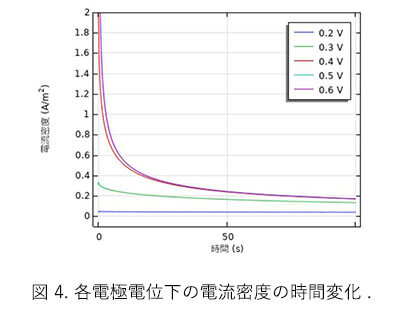
2) 大堺利行,加納健司,桑畑 進,「ベーシック電気化学」,化学同人 (2000) 110.
3) A.J. Bard and L.R. Faulkner, Electrochemical Methods―Fundamentals and Applications, 2nd Ed.”, Wiley, New York (2001) 195.
4) 寺沢寛一,「自然科学者のための数学概論 (増訂版 」,岩波書店 (1954) 158.
5) 犬井鉄郎,石津武彦、「 複素関数論 <東京大学基礎工学 7>」 、東京大学出版会 (1966) 174.
最初、過電圧が負の大きな值をとり、系全体がバルク濃度の還元体で占められている状態にあって、その状態が維持されているとする。そこに時刻 $t=0$ から $t=t_{d}$ の間、正の一定の過電圧 $\eta=$ $E-E_{0}>0$ を加えた場合の系の電流の時間変化を観測、即ち電位ステップクロノアンペロメトリー (PSCA)の実験を行なう。過電圧 $\eta$ の下での電極反応速度は、式(1)が不可逆反応なので、その反応速度は Buttler-Volmer 式1) $$ k_{0}^{+} \cdot C_{\mathrm{R}} \cdot \exp \left(\frac{\alpha n F}{R T}\left(E-E_{0}\right)\right)-k_{0}^{-} \cdot C_{0} \cdot \exp \left(-\frac{(1-\alpha) n F}{R T}\left(E-E_{0}\right)\right) (2) $$ の酸化項のみ(Anode Tafel 式)によって、$k_{0}^{+} を k_{0}$ に書き換え、 $$ k_{0} \cdot C_{\mathrm{R}} \cdot \exp \left(\frac{\alpha \eta F}{R T}\left(E-E_{0}\right)\right)=k_{0} \cdot C_{\mathrm{R}} \cdot \exp (\eta / A) (3) $$ と表せる。ここでRは気体定数、$T$ は熱力学温度、$C_{\mathrm{R}}$ は電極界面での還元体の濃度、$A=\frac{R T}{\alpha n F}$ である。ここで速度定数 $k_{0}$ は参照交換電流密度 $i_{0, \mathrm{ref}}$ との間にファラデー定数 $F を$ 用い、 $$ i_{0, \text { ref }}=n F k_{0} (4) $$ の関係がある。酸化体は上述のように系の電気化学に関係しないので、系の濃度としては還元体の濃度だけを考えれば良い。 本例題は、COMSOL Multiphysics の電気化学モジュールを利用し、次の Anode Tafel 式 $$ i_{\mathrm{loc}}=i_{0} \times 10^{\eta / \mathrm{A}_{a}} (5) $$ になった。 $i_{0}$ は交換電流密度、$i_{0}=i_{0, \mathrm{ref}} \cdot C_{\mathrm{R}}, \mathrm{A}_{a}=2.303 \times \mathrm{A}$ である。
($𝑥=exp (𝜂/𝐴)$であれば, $𝜂/𝐴=ln(𝑥)=2.303log (𝑥)$になり,そして, $𝑥= 10^{\eta / \mathrm{(2.303×A)}}$ であった。)
計算は、1 次元モデルを用いて行った。セルの長さ $\mathrm{L}=0.1 \mathrm{~cm}$, 還元体のバルク濃度 $c_{\text {bulk }}=1$ $\mathrm{mmol} / \mathrm{L}$, 拡散係数 $\mathrm{D}=1 \times 10^{-9} \mathrm{~m}^{2} / \mathrm{s}$, 熱力学温度 $\mathrm{T}=298.15 \mathrm{~K}$, 系の持続時間 $\mathrm{td}=100 \mathrm{~s}$, 電極界面 の反応速度定数 $\mathrm{k}_{0}=1 \times 10^{-6} \mathrm{~cm} / \mathrm{s}$, 初期電極電位 $\mathrm{E}_{0}=-1 \mathrm{~V}$, 印加電極電位 $\mathrm{E}_{1} は 0.3 \mathrm{~V}$, とした。
本書では、解析モデルおよび、2章以後に図 1 4 の解析結果を作成する手順を示す。 濃度分布の時間変化を図 1 に示す。 $t=0 \mathrm{~s}$ では全領域がバルク濃度であったが、時間経過とともに左端の電極から濃度が減少し、それが拡散によって右側の領域に広がっていく様子が見てとれる。右端は境界条件によりバルク濃度に固定されている。 領域を 5 等分した各点と両端の濃度の時間変化を図 2 に示す。右端では濃度はバルク濃度で一定であるが、電極に近づくにつれて、ある時刻から濃度の減少が始まることが分る。


電流密度の時間変化を図 3 に示す,最初は大きな電流が流れ,それが時間とともに減衰していく。 図 1 から読み取った $100 \mathrm{~s}$ 経過後の左端電極付近の濃度勾配はおよそ $1.3 \times 10^{3} \mathrm{~mol} / \mathrm{m}^{4}$ なので、
これと拡散係数 $10^{-9} \mathrm{~m}^{2} / \mathrm{s}$ の積 即ち $1.3 \times 10^{-6} \mathrm{~mol} /\left(\mathrm{s} \mathrm{m}^{2}\right)$ が電極付近に単位面積、単位時間当たり拡散によって流れ込む還元体の物質量となる。そしてこれが電極反応で単位面積単位時間当たり消失する還元体の物質量と釣り合っているので、$n(=1)$ とファラデー定数とを掛けると,電極電流がおよそ $0.13 \mathrm{~A} / \mathrm{m}^{2}$ と求められる。これは図 3 から読み取った $100 \mathrm{~s}$ 経過後の電流密度の值とよく一致している。 図 3 には解析解も示されている。 解析解は次式の上うに与えられている ${ }^{2,3)}$. $$ i=n F k C \exp \left(\frac{k^{2} t}{D}\right) \times \operatorname{erfc}\left(k \sqrt{\frac{t}{D}}\right) (6) $$ 但し, $$ k=k_{0} \cdot \exp \left(\frac{\alpha n F}{R T}\left(E-E_{0}\right)\right) (7) $$ と置いた。また $C$ は還元体の初期濃度、erfc は余誤差関数である。 実際の計算に当たって、式(7)の指数関数部分がオーバーフローする場合には、余誤差関数の漸近展開 ${ }^{4,5)}$ $$ \operatorname{erfc}(x) \approx \frac{e^{-x^{2}}}{\sqrt{\pi}}\left(\frac{1}{x}-\frac{1}{2 x^{3}}+\frac{3}{4 x^{5}}-\frac{15}{8 x^{7}}+\cdots\right) (8) $$ を用いて、$x=k \sqrt{\frac{t}{D}}>15$ に対しては、$\frac{15}{8 x^{6}}<1.646 \times 10^{-7}$ が成立するので, $$ \operatorname{erfc}\left(x^{2}\right) \operatorname{erfc}(x) \approx \frac{1}{x \sqrt{\pi}}\left(1-\frac{1}{2 x^{2}}+\frac{3}{4 x^{4}}-\cdots\right) (9) $$ が 6 桁目までは正しい值を与える。このとき式(6)は $$ i \approx n F C \sqrt{\frac{D}{\pi t}}\left(1-\frac{1}{2 x^{2}}+\frac{3}{4 x^{4}}\right) (10) $$
となる。式(10)により、$𝑥→∞$の極限では式(6)が Cottrell式$i=n F C \sqrt{\frac{D}{\pi t}}$になることを理解できる。
電極電位 $\mathrm{E}_{1}$ を $0.2 \mathrm{~V}$ から $0.6 \mathrm{~V}$ まで $0.1 \mathrm{~V}$ 刻みに変元て電流密度の時間変化を見たものは図 4 で ある。 電極電位を上げていくと、式(3)に従って電極反応速度が大きくなり電流密度も増大するが、0.5 $\mathrm{V}$ と $0.6 \mathrm{~V}$ が殆ど重なっていることから、ある一定值に収束していくことが分る。この収束先は、電極の付近の濃度が一瞬にしてゼロとなったとして拡散方程式を解くと得られる Cottrell の式である。

参考文献
1) 外島忍、佐々木英夫、「電気化学」、オーム社 (1964) 143.2) 大堺利行,加納健司,桑畑 進,「ベーシック電気化学」,化学同人 (2000) 110.
3) A.J. Bard and L.R. Faulkner, Electrochemical Methods―Fundamentals and Applications, 2nd Ed.”, Wiley, New York (2001) 195.
4) 寺沢寛一,「自然科学者のための数学概論 (増訂版 」,岩波書店 (1954) 158.
5) 犬井鉄郎,石津武彦、「 複素関数論 <東京大学基礎工学 7>」 、東京大学出版会 (1966) 174.
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。