現在の定常状態におけるシミュレーション研究では、昔から研究されているアーク溶接などの現象については多く行われており、報告も多数ある。弊社開発したモデル「アーク溶接における MHD 解析」では過渡計算が行われたが、流れ計算を含まらないため、簡易モデルと言われる条件でシミュレーションされた。 MHD (MagnetoHydroDynamics : 電磁流体力学) 解析は、局部熱平衡近似として行われる手法がよく使われる。熱流体、電磁流体の挙動は質量保存則、運動量保存則、エネルギー保存則、電流連続の式、オームの法則により支配される。アークプラズマにおける電子、イオン、中性粒子の輸送は解かず、伝熱、流体、電磁気を解く。ガスを放電させて大電流を流すと、瞬間的に放電路が熱せられて局部的に急激な圧力上昇が起こり、そこから衝撃波が発生すると示唆させる。衝撃波の形成とともに放射損失が非常に重要になるが、このシヨックフロントを解決するのは計算上で非常に困難である。問題の複雑さを軽減するために、ここでは、追加の安定化方法を採用し、アーク溶接における MHD 非定常解析の計算手法を示す。それによって時間変化ごとにガス流と加熱の挙動および電磁場分布を捉える。

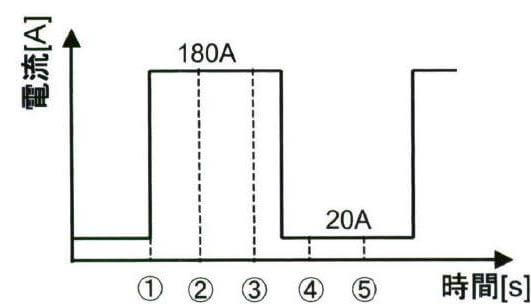
本例題は、図 1 のように、「アーク溶接における MHD 解析」と同じ形状を利用し、流れおよび磁場の計算を追加しており、さらに COMSOL の電磁流体力学インターフェースを導入する。ローレンツカおよび起電力の計算も含まる。図 2 に示した周波数$20 \mathrm{~Hz}$のパルス電流 $I_{\mathrm{p}}$ を採用した。

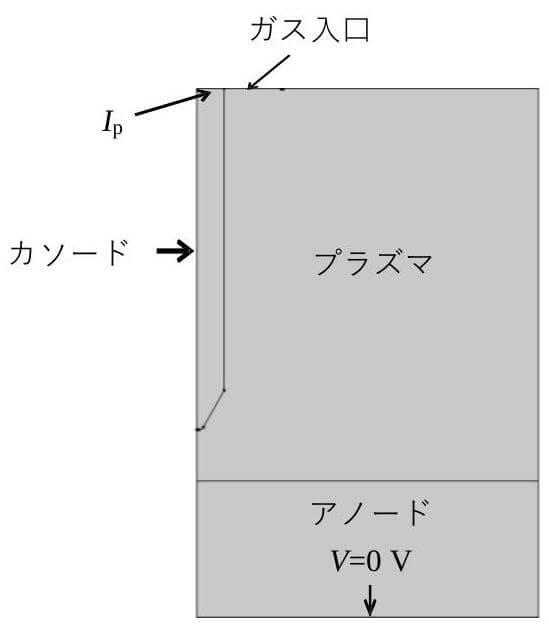
プラズマ放電の熱源 $Q$ を伝熱（流体）インターフェースに連成させて、支配方程式を式(1)に示す。

$$
\begin{gathered}
\rho C_{p} \frac{\partial T}{\partial t}+\rho C_{p} \mathbf{u} \cdot \nabla T+\nabla \cdot \mathbf{q}=Q \\
\mathbf{q}=-k \nabla T
\end{gathered} \tag{1}
$$

ここで、 $\rho$ は密度、 $C_{p}$ は比熱容量、 $T$ は温度、 $\mathbf{u}$ は流速、 $\mathbf{q}$ は熱流束、 $k$ は熱伝導率である、熱源 Qは、マルチフィジックス機能によって以下に定義される。

1）抵抗加熱 (オーム加熱): $Q=\mathrm{J} \cdot \mathrm{E}$
2）正味放射損失 $Q_{\text {rad }}$
3）エンタルピー輸送

$$
\frac{\partial}{\partial T}\left(\frac{5 k_{B} T}{2 q}\right)(\nabla T \cdot \mathrm{J})
$$

アノードとカソード境界熱源 $Q_{b}$ は式(2)で表される。

$$
\begin{array}{ll}
-\mathbf{n} \cdot(-k \nabla T)=Q_{b} & \\
Q_{b}=|\mathbf{J} \cdot \mathbf{n}| \phi_{s} & \text { アノード } \\
Q_{b}=-\left|\mathbf{J}{\text {elec }}\right| \phi{s}+\left|\mathbf{J}{\text {ion }}\right| V{\text {ion }} & \text { カソード }
\end{array} \tag{2}
$$

ここで、$\phi_{s}$ は表面仕事関数、 $V_{\text {ion }}$ はプラズマの電離電位、 $\mathbf{J}{\text {elec }}$ と $\mathbf{J}{\mathrm{ion}}$ はそれぞれ電子とイオンの電流密度である。
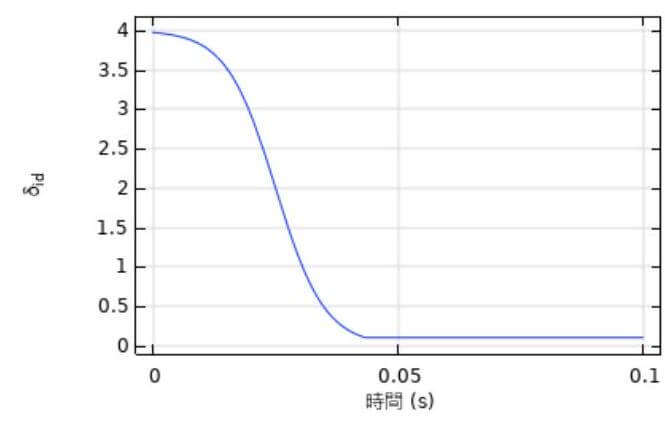
本例題は、MHD非定常解析手法を示す。図2 に示すパルス電流は、周期ごとに20Aのベース電流から、180Aのピーク電流まで $120 \mathrm{~A}$ 電流值が上がるため、毎回生成されたアーク放電路にさらに熱せられる、局部的に急激な圧力上昇が起こることで、計算は困難になる。ここで、追加の安定化方法として、COMSOLの等方性拡散という不整合安定化手法を利用した。この手法は人工的な拡散を追加するため、問題の解析精度に影響を与えるが、図3に示したチューニングパラメーター $\delta_{\mathrm{id}}$ のようにこの影響を最小限に抑える。等方性拡散項は式(3)に定義される。

$$
c_{\text {art }}=\nabla \cdot\left(\delta_{\text {id }} h|\rho \mathbf{u}| \nabla \mathbf{u}\right) \tag{3}
$$

ここで、 $\delta_{\mathrm{id}}$ はチューニングパラメーター、hは局部メッシュのサイズである。
本書では、解析モデルおよび、2 章以後に図 4 の解析結果を作成する手順を示す。

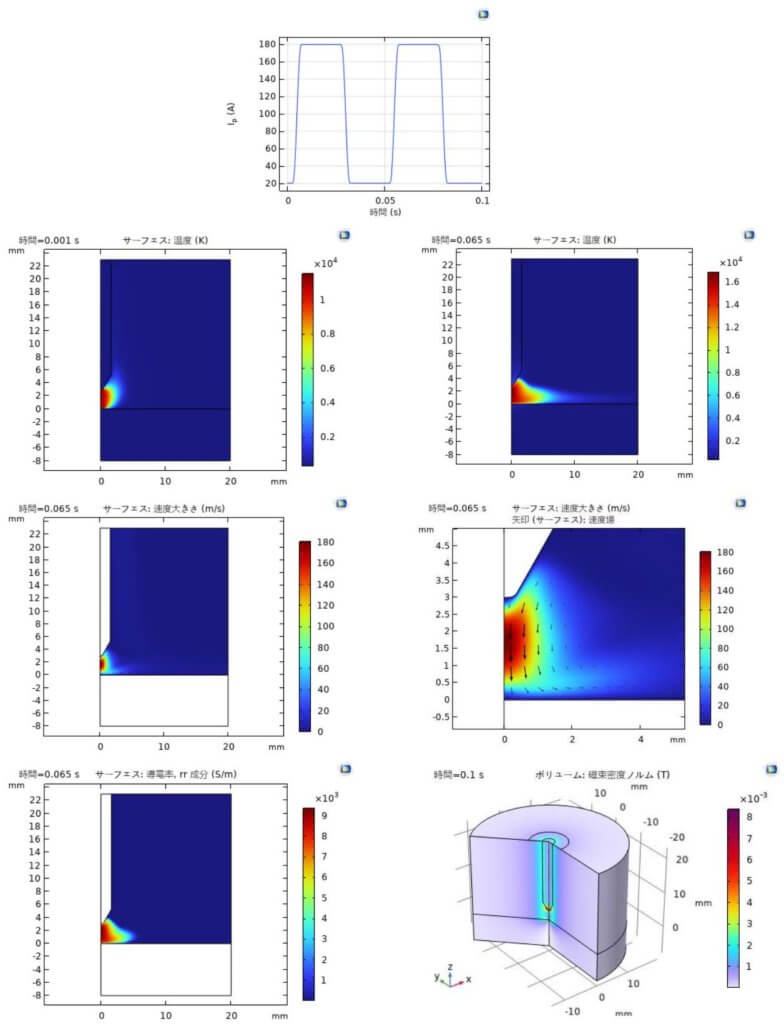
溶接時間を2周期、 $0.1 \mathrm{~s}$ とて計算が行われた。第1周期でアークが形成され、第2周期以後は安定したパルス放電になると考元られる。図4は溶接電流、温度、速度、ガスの導電率および磁束密度の計算結果である。視覚的に示すため、異なる時刻での結果は示された。また、ガスの導電率の結果表示にはガス以外の部分の導電率が0に設定された。

参考文献

1） 平田好則, パルスアーク溶接, 溶接学会誌, Vol. 71, No. 5, 2002: 389-404.

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。