従来のリチウムイオン電池には可燃性の有機電解液が含まれており、発火・爆発事故が多く報告されている。有機電解液を無機固体電解質に置き換えた全固体電池は、安全性、高エネルギー密度および長寿命が期待される${ }^{1)}$。全固体電池は可燃性の有機電解液を不燃性の無機固体電解質に置き換えた安全性の高い電池であり、薄膜型とバルク型に大別されている。薄膜型全固体電池では、気相法を用いて薄膜を積層することにより、良好な電極-電解質間の固体界面接合を実現している。ここで、薄膜型全固体電池（以下、全固体電池と略称）を考慮する。
交流インピーダンス測定法は、試料電池へ微少な交流電流を流して、基準交流波と比較することで、試料電池のインピーダンスを複素インピーダンス（インピーダンスの大きさと位相）として求める方法である。交流の周波数を少しずつ変化させ、各周波数で得られるインピーダンスと位相差を複素平面上にプロットすることで電池の内部インピーダンスを視覚的に明確化できる。複素インピーダンスプロットはナイキストプロットもしくはコールコールプロットと一般に呼ばれる、コールコールプロットとは、誘電体の複素誘電率をさまざまな周波数に対して複素平面にプロットしたものをいうため、ここでは、電気化学系の複素インピーダンスプロットはナイキストプロットと呼ぶ。図 1 に単純な酸化還元反応 $\left(0+n \mathrm{e}^{-} \rightleftharpoons \mathrm{R}\right)$ の理論的なナイキストプロットとランドルス型等価回路を示す。

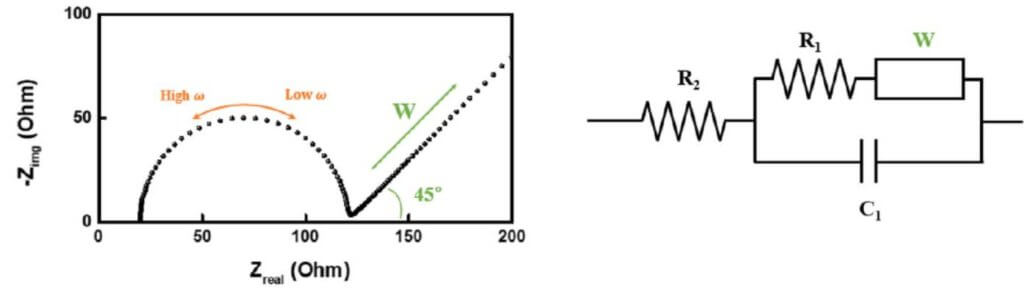
図 1 におけるWはワールブルグインピーダンスである。電極反応を伴う場合は、電極側の電子が電解質側の分子やイオンに受け渡される。この電極反応がバトラー・ボルマー式を使えば、荷移動過程に関係する電荷移動抵抗 $R_{1}$ と、 物質移動過程に関係するワールブルグインピーダン スWの直列回路で表せる。両者を合わせてファラデーインピーダンスと呼ぶ ${ }^{2)}$。
交流インピーダンス $Z$ は、複素数で表され、実部と虚部をされぞれ $Z_{\mathrm{Re}}$ と $Z_{\operatorname{lm}}$ で表すと、虚数単位をjとして次式に書ける。

$$
\dot{Z}=Z_{\mathrm{Re}}-j Z_{\mathrm{lm}} \tag{1}
$$

ベクトル亡்の大きさ $|\dot{Z}|$ と位相角 $\phi$ は次の内容をもつ。

$$
|\dot{Z}|=\sqrt{Z_{\mathrm{Re}}^{2}+Z_{\mathrm{lm}}^{2}} \tag{2}
$$

$$
\tan \phi=\frac{Z_{\mathrm{lm}}}{Z_{\mathrm{Re}}} \tag{3}
$$

$$
\sigma=\frac{R T}{\sqrt{2} n^{2} F^{2} A}\left(\frac{1}{\sqrt{D_{\mathrm{o}}} c_{\mathrm{o}}}+\frac{1}{\sqrt{\bar{D}{\mathrm{R}}} c{\mathrm{R}}}\right) \tag{4}
$$

図 1 に示したように、周波数が高い場合には、化学種の拡散によるワールブルグインピーダンスWの寄与は無視できるようになる。軌跡は、実軸上の $Z_{\mathrm{Re}}=R_{2}+R_{1} / 2$ を心とする半径 $R_{1} / 2$ の 半円を描く。一方、周波数が低いときは逆に電荷移動抵抗の寄与が減り、物質移動に由来するワールブルグインピーダンスWが支配的となる。その軌跡は、実軸の $R_{2}+R_{1}-2 \sigma^{2} C_{1}$ を切片とした傾き 1 の直線となる。 $\sigma$ は次式の内容をもつ。

ここで、$D_{\mathrm{o}}, D_{\mathrm{R}}$, ならびに $c_{\mathrm{o}}, c_{\mathrm{R}}$ はそれぞれ溶液中の酸化体と還元体の拡散係数と電極表面濃度、$n$ は関与電子数、$F$ はファラデー定数である。電荷移動抵抗 $R_{1}$ と交換電流 $i_{0}$ は次式で結びつく。

$$
R_{1}=\frac{R T}{F i_{0}} \tag{5}
$$

この計算例は、COMSOL Multiphysicsによる全固体電池のインピーダンス解析を行う。まず、放電曲線の計算結果を試験値 ${ }^{3}$ と比較することで、全固体電池の解析モデルを検証する。次に交流インピーダンス測定法と同じ手法で微少な交流電流を流して全固体電池のインピーダンスを 考察する。

計算ジオメトリは、図 2 に示すような、正極を $\mathrm{LiCoO}_{2}$ 、負極を $\mathrm{Li}$ 、固体電解質をLiPONとする 全固体電池の1Dモデルである。固体電解質と正負極領域との間の界面で起こった電極反応は、以下のように考慮される。

負極と正極の表面化学反応は式(1)と(2)で表われる。

$$
{Li} \leftrightarrow \mathrm{Li}^{+}+e^{-} \tag{6}
$$
$$
{LiCoO}_{2} \leftrightarrow \mathrm{Li}_{1-x} \mathrm{CoO}_{2}+xLi^{+}+xe^{-} \tag{7}
$$

これらの電気化学反応はバトラー・ボルマー式でモデル化される ${ }^{3)}$ 。

電解質内の化学反応を電離反応 $\mathrm{Li}^{0} \leftrightarrow \mathrm{Li}^{+}+\mathrm{n}^{-}$とする ${ }^{3}$。 ここで $\mathrm{Li}^{0}$ は酸素と結合した動かない リチウム, $\mathrm{n}^{-}$は非補償型の負の電荷である。 $\mathrm{Li}^{+}$と $\mathrm{n}^{-}$の輸送計算はネルンスト・プランク方程式

$$
\mathbf{N}{i}=-D{i} \nabla c_{i}+\frac{z_{i} F}{R T} D_{i} c_{i} \nabla \phi_{l} \tag{9}
$$

で行われる。ここで, $c_{i}$ と $D_{i}$ はイオンの濃度と拡散係数, $z_{i}$ はイオン価数, $F$ はファラデー定数, $T$ は絶対温度, $R$ は気体定数, $\phi_{l}$ は電解質電位である。電解質における電流密度分布は次式の内容をもつ。

$$
\mathbf{i}{l}=F \sum{i} z_{i}\left(-D_{i} \nabla c_{i}-z_{i} u_{m, i} F c_{i} \nabla \phi_{l}\right) \tag{10}
$$

正極内のリチウム種の輸送はフィックの法則

$$
\mathbf{N}{\mathrm{Li}}=-D{\mathrm{Li}} \nabla c_{\mathrm{Li}} \tag{11}
$$

に従う。 $c_{\mathrm{Li}}$ と $D_{\mathrm{Li}}$ はリチウム種の濃度と拡散係数である。計算では, 式(9)と(11)が質量保存式

$$
\frac{\partial c_{k}}{\partial t}+\nabla \cdot \mathbf{N}{k}=R{k} \tag{12}
$$

に代入される。 $k$ は $i$ と $\mathrm{Li}$ を意味する。 $R_{k}$ は反応速度である。

本書では解析モデルおよび、図 3 の解析結果を作成する手順を示した。

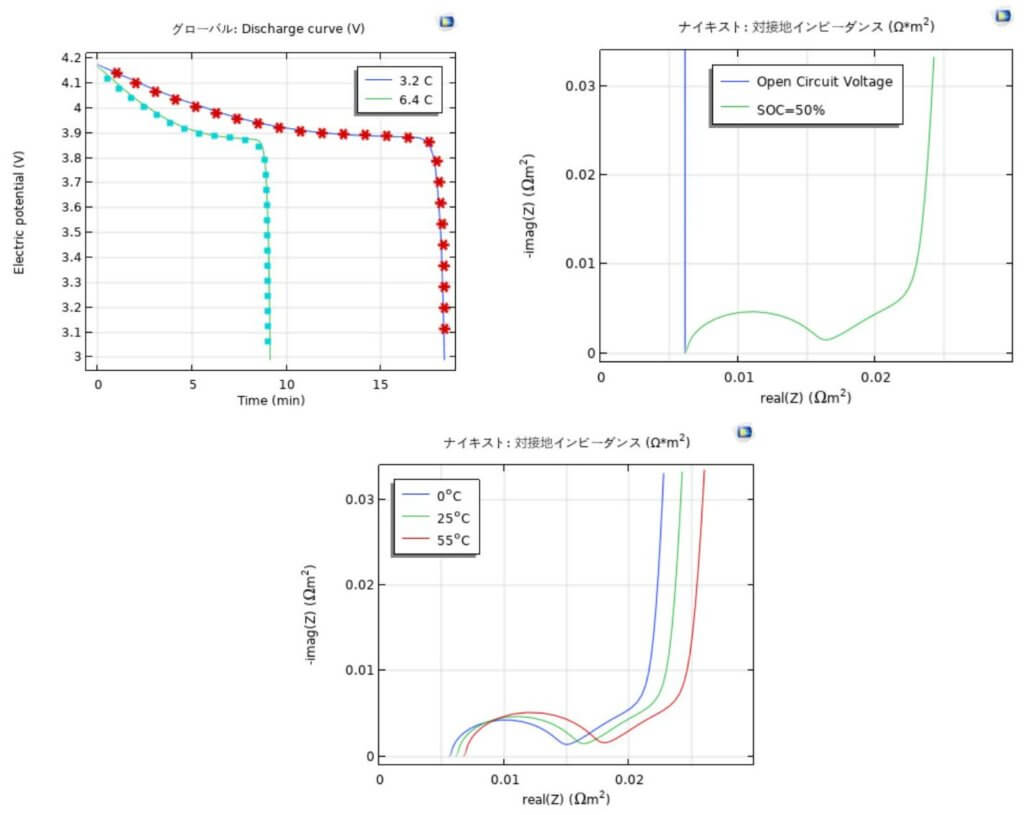
図3 に全固体電池の放電曲線およびインピーダンスを示している。放電曲線の計算値は試験値（象徴）3 とよく一致したことで、全固体電池の解析モデルは検証された。電池に負荷をかけていない（$OCV$）とかけている（$S OC=50% 50%$）状態のナイキストプロットが示された。全固体電池に負荷をかけていない場合（$OCV$）は、等価回路が電解質側の抵抗𝑅 2 と電気二重層の静電容量𝐶 1 の直列回路になると考えられる。その際、インピーダンスの軌跡は虚数軸に平行な直線となり、周波数が高くなるほど実軸切片に近づいていく。従来のリチウムイオン電池における多孔質電極内でのイオン抵抗のインピーダンスへの影響が薄膜型全固体電池に発生しないことを検証した。温度に依存する全固体電池のナイキストプロットも示された。

参考文献

1) 佟立柱，福川真，リチウムイオン電池・全固体電池のシミュレーション技術－ Li イオンの輸送と反応に基づく電気化学モデルから集中パラメータによる電池モデルまで－，計算工学, Vol. 25, No. 4, 4145-4150 (2020).
2) 渡辺 正, 片山 靖, 電池がわかる電気化学入門, オーム社 (2011).
3) D. Danilov, R. A. H. Niessen, and P. H. L. Notten, Modeling All-Solid-State Li-Ion Batteries, J. Electrochem.Soc., Vol. 158, No. 3, A215–A222 (2011).

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。