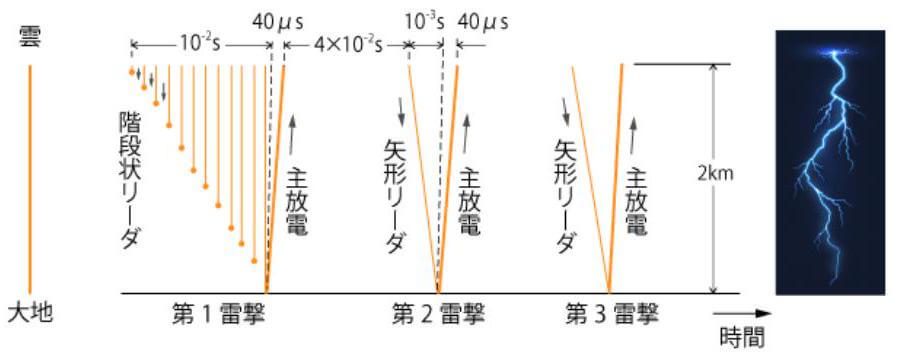
雷放電は、雲から大地に放電する対地放電(いわゆる落雷、Ground Flash)と雲の中で放電が完結する雲放電(Cloud Flash)の2種に大別する。そしてさらに、落雷は雲内の正電荷が中和される正極性落雷と負電荷が中和される負極性落雷の2種に分けられる。これらの各種放電の比率は、季節や積乱雲のタイプなどによって大きく変化する。落雷は、放電開始(Initiation)、リーダ(Leader)、帰還雷撃(Return Stroke)、ダートリーダ(Dart Leader)、後続雷撃(Subsequent Return Stroke)などの各過程から構成されている。落雷は約 $10^{5} \mathrm{~m} / \mathrm{s}$ 程度で大地に向けて放電は進展する。これをステップトリーダ(Stepped Leader)と呼ぶ。地表面に達すると、強い発光を伴って、同じ経路を光速の3分の1程度の速度で地表から上空に放電が進展する。これを第一帰還雷撃(First Return Stroke)と呼ぶ。その時、平均 $30 \mathrm{kA}$ 程度の電流が流れる。その後、再び、同様な経路を、積乱雲からリーダにした。しかし、速度が一桁ほど速い(107 $\mathrm{m} / \mathrm{s}$ 程度)ダートリーダと呼ばれる放電が下降し、地表面付近に達すると再び帰還雷撃に似た大電流が流孔る。これを先ほどの第一帰還雷撃に対して、後続雷撃(Subsequent Return Stroke)と呼んでいる。こうした過程が何度も繰り返され、一つの雷放電が完結する ${ }^{1)}$。 図1 亿落雷の仕組みを示す。帰還雷撃と後続雷撃とも主放電が呼ばれる。
高圧架空電線路は長距離にわたって自然の厳しい条件にさらされるため、雷撃を受ける機会も多く、この雷撃による異常電圧が送電線に入り、伝播して発変電所などの設備に影響を与える。 また、送電線に直接落雷するとその膨大な電圧のため、各相の碍子連がすべてフラッシオーバしたことで再送電が不能になる場合がある。現在、複合絶緑体とした碍子連の絶緑評価は、数値シミュレーションを含んで、実験室試験条件で行われたが、これらの報告は複合絶緑体単体に対して行った研究である ${ }^{2,3)}$ 。雷放電は自然界に存在する $\mathrm{km} $にも及ぶ超長ギャップ放電であり、その形態は、数センチ程度のギャップ長の実験室放電とは大きく異なる。図2 に送電線路を示している。複合絶緑体(碍子)が送電線路における鉄塔に実装されるため、3D解析が必要になると考えられる。そこで本例題は、COMSOL MultiphysicsのRFモジュールを用いて雷撃を受けた時の高圧架空電線路における複合絶縁体(碍子)の絶縁評価を行った。落雷において負極性落雷が $90 \%$程度 ${ }^{4)}$ であるため、ここでは、負極性落雷による雷の電磁パルス(LEMP:Lightning Electromagnetic Pulse)攻撃に対して複合絶緑体(碍子)の電磁場解析を行った。

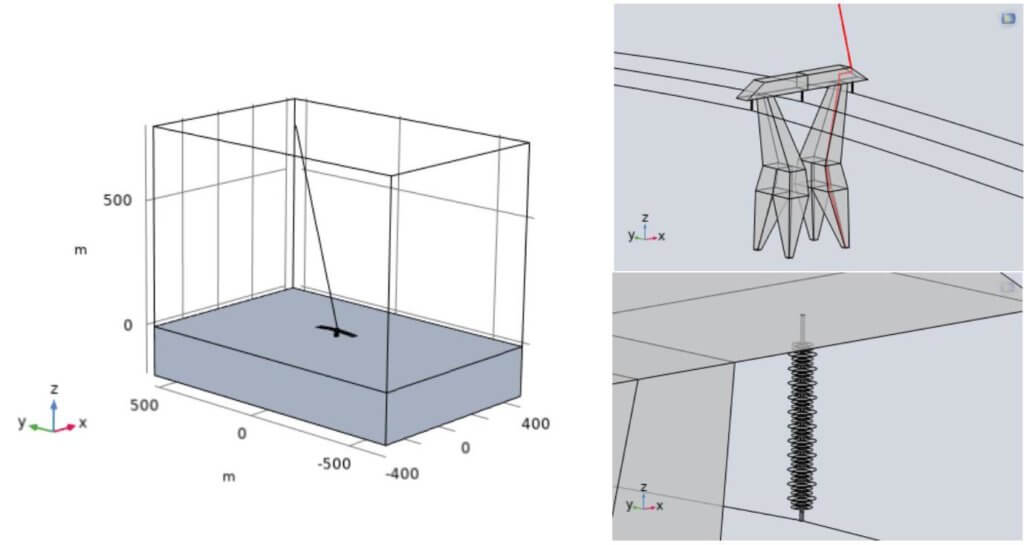
解析モデルは図3に示す。高圧配電線では避雷器の密な取り付けにより、誘導雷による雷事故は少なく、直撃雷によるそれの割合が高い。そのため、ここでは、鉄塔に直撃雷が発生することをモデリングする。骨組み構造から構成される鉄塔は導電体として一体化される。主放電とした第一帰還雷撃は後続雷撃より2~3倍高い電流 ${ }^{4)}$ が流れることで、第一帰還雷撃による解析を考慮する。帰還雷撃工学モデル ${ }^{5)}$ は以下に示される。
$$
i= \begin{cases}\frac{i_{\max }}{\eta} \cdot \frac{\left(\frac{t_{d}}{T}\right)^{n}}{1+\left(\frac{t_{d}}{T}\right)^{n}} \exp \left(-\frac{t_{d}}{\tau}\right), t_{d}=t-\frac{s}{V_{p}} & t_{d}>0 \\ 0, & t_{d}<0\end{cases} \tag{1}
$$
ここで、 $i$ は帰還雷撃電流、 $i_{\max }$ は雷パルス振幅、 $T$ は雷パルス立ち上がり時の定数、 $\tau$ は雷パル ス減衰時の定数、 $\eta$ と $n$ は雷パルスのパラメーター、$s$ はパラメーター化パス、 $V_{p}$ はパルス速度である。
表 1. 帰還雷撃工学モデルのパラメーター ${ }^{5)}$
| $i_{\max }(\mathrm{kA})$ | $T(\mu s)$ | $\tau(\mu s)$ | $\eta$ | $n$ | $s$ | $V_{p}$ |
|---|---|---|---|---|---|---|
| 30 | 0.454 | 143 | 0.993 | 10 | $s 1$ | $\sim \mathrm{c}_{-}$const $/ 3$ |
各パラメーターは表1 に示される。 $s 1$ はパラメーター化パスとしたCOMSOL変数、c_constは光速、COMSOL組み込み定数である。
本例題は、COMSOL MultiphysicsのRF モジュールの電磁波(時間発展)インターフェースを利用した。磁気ベクトルポテンシャルの波動方程式を時間領域で解く。一体化された鉄塔の表面は完全導体(PEC: Perfect Electric Conductor)を設定することで、鉄塔内での帰還雷撃電流経路は鉄塔への雷撃点と接地点の間に任意で設定可能であると考えられる。本モデルの帰還雷撃電流経路は図4 に示される。
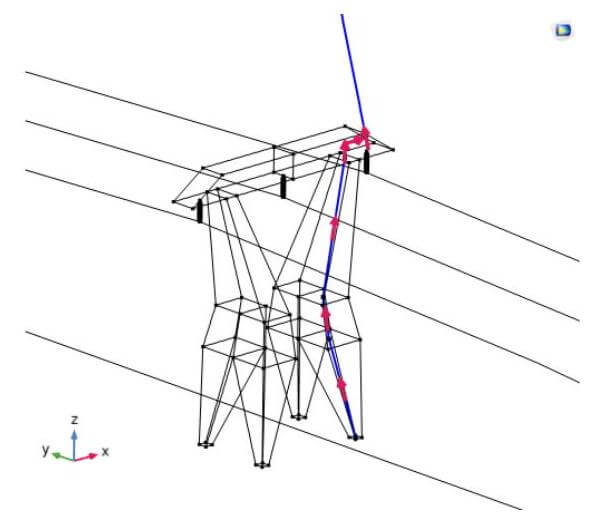
本書では、モデルおよび、2章以後に図5 と図6 の解析結果を作成する手順を示す。
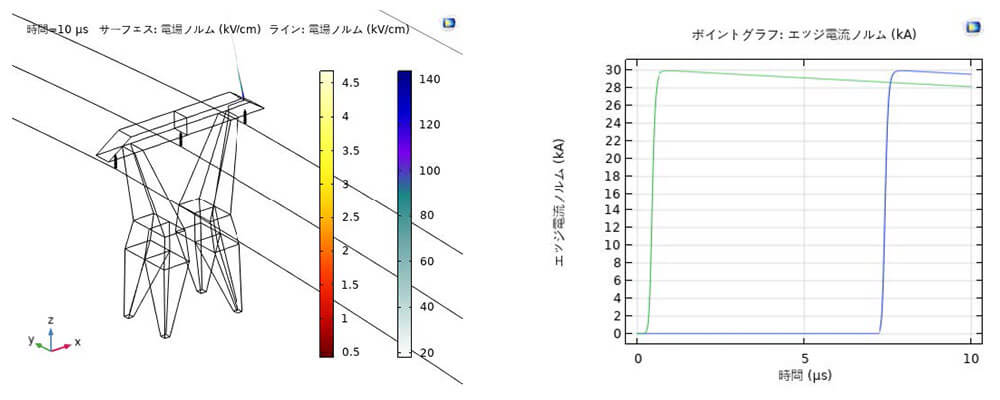
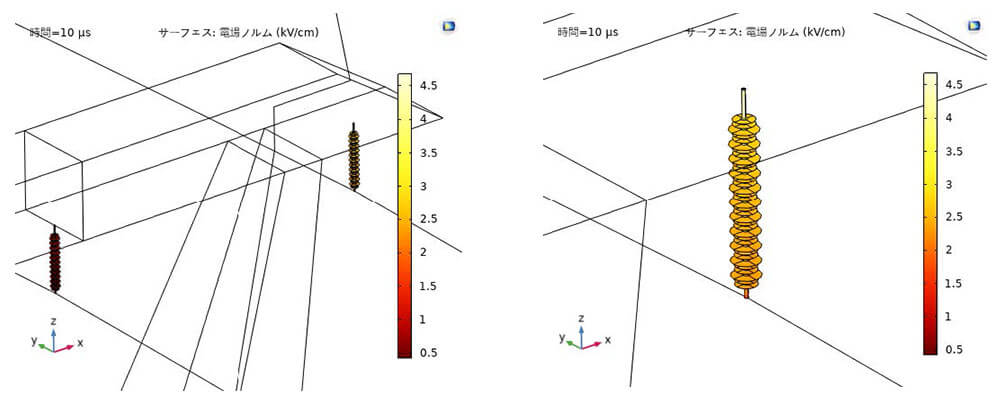
図 $5 に 10 \mu \mathrm{s}$ 後の複合絶緑体(碍子)表面と落雷経路における誘導電場および落雷の接地点と開始点の帰還雷撃電流を示している。鉄塔への雷撃点に最大 $144 \mathrm{kV} / \mathrm{cm}$ の誘導電場が発生した。複合絶緑体表面には、最大 $4.67 \mathrm{kV} / \mathrm{cm}$ の誘導電場があった。帰還雷撃電流では、$7 \mu \mathrm{s}$ 後に落雷開始の放電雲に着く、 $7.9 \mu \mathrm{s}$ 後に最大値 $30 \mathrm{kA}$ に上昇した。図6 は図5 を拡大した $10 \mu \mathrm{s}$ 後の複合絶縁体表面での誘導電場分布である。複合絶縁体の芯棒の上部に最大誘導電場が示された。水滴が付着した高圧絶緑体表面にコロナを発生させる電場は $10 \mathrm{kV} / \mathrm{cm}$ 以下であり、最小限のコロナを確保するための最大許容電場は $4.2 \mathrm{kV} / \mathrm{cm}$ であることが既に報告された ${ }^{6)}$。複合絶緑体(碍子)にシールドリングなどを追加して複合絶緑体における最大誘導電場を減らせる必要性を示唆している。
参考文献
1) 牛尾知雄,日本物理学会誌,Vol. 71, No. 4, 2016: 235–238.
2) X. Zhao, X. Yang, J. Hu, et al., IEEE Trans. Dielectr. Electr. Insul., Vol. 26, No. 4, 2019: 1253-1259.
3) A. Al-Gheilani, W. Rowe, Y. Li, and K.L. Wong, Energy Procedia, Vol. 110, 2017: 95–100.
4) Y. Baba and V.A. Rakov, Present Understanding of the Lightning Return Stroke, H.D. Betz, et al.(eds.), Lightning: Principles, Instruments and Applications, Springer Science+Business Media B.V. 2009.
5) F. Heidler, J. Cvetic, Eur. Trans. Electr. Power (ETEP), Vol. 12, No. 2, 2002: 141-150.
6) A.J. Phillips, D.J. Childs, and H.M. Schneider, IEEE Trans. Power Del., vol. 14, No. 3, 1999: 1081-1089.
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。