雷放電は、雲から大地に放電する対地放電（いわゆる落雷、Ground Flash）と雲の中で放電が完結する雲放電（Cloud Flash）の2種に大別するそとしてさらに、落雷は雲内の正電荷が中和される正極性落雷と負電荷が中和される負極性落雷の2種に分けられる。これらの各種放電の比率は、季節や積乱雲のタイプなどによって大きく変化する。
落雷は、放電開始（Initiation）、リーダ（Leader）、帰還雷撃（Return Stroke）、ダートリーダ（Dart Leader）、後続雷撃（Subsequent Return Stroke）などの各過程から構成されている。落雷は 約 $10^{5} \mathrm{~m} / \mathrm{s}$ 程度で大地に向けて放電は進展する。これをステップトリーダ（Stepped Leader）と呼ぶ。地表面に達すると、強い発光を伴って、同じ経路を光速の3分の1程度の速度で地表から上空に放電が進展する。これを第一帰還雷撃（First Return Stroke）と呼ぶ、その後、再び、同様な経路を、積乱雲からリーダにした。しかし、速度が一桁ほど速い（$10 ^{7} \mathrm{m} / \mathrm{s}$ 程度）ダートリーダと呼ばれる放電が下降し、地表面付近に達すると再び帰還雷撃に似た大電流が流れる。これを先ほどの第一帰還雷撃に対して、後続雷撃（Subsequent Return Stroke）と呼しでいる。こうした過程が何度も繰り返され、一つの雷放電が完結する ${ }^{1) }$ . 図 1 に落雷の仕組みを示す。帰還雷撃と後続雷撃とも主放電が呼ばれる。

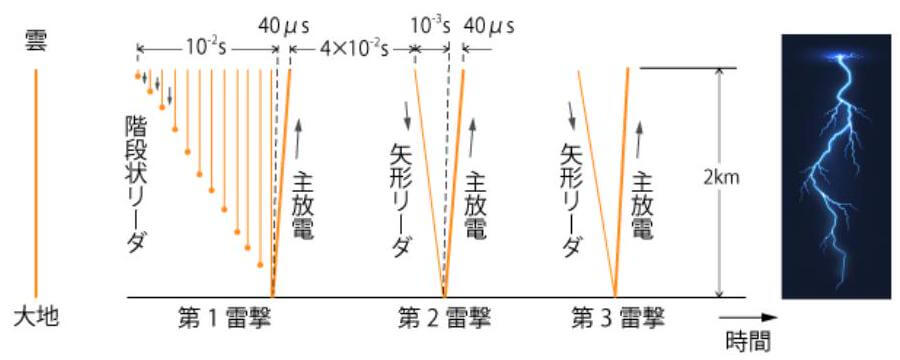
第一帰還雷撃（First Return Stroke）を形成する前に、階段状（ステップトリーダ）の雷リーダが雲から発生し、空気を通し地表面に進展する。雷リーダが地表面に近づくに達すると、強い電場によって地上構造物が応答リーダを放射する。雷リーダの先端と地上構造物の間の距離は落雷距離と呼ばれる。本例題は、避雷設計の国際規格であるIEC62305で定義されている避雷システム設計ルートに基づいて、応答リーダを放射する前に雷リーダにさらされる地上構造物の電界の解析を行う。
ローリングスフィア法（Rolling sphere method）は避雷システム設計ルートの1つである. 図 2 に示したように地上構造物に取り付けられた回転球の半径 $R$ は落雷距離に等しいと考えられる ${ }^{2) }$。半径Rは帰還雷撃のピーク電流の関数であり、次のように表される ${ }^{2) }$ .

$$
R=1.9 \times I_{\text {peak }}^{0.9} \tag{1}
$$

ここで、Rはローリングスフィア半径 $(\mathrm{m}), I_{\mathrm{peak}}$ は帰還雷撃のピーク電流（kA）である.

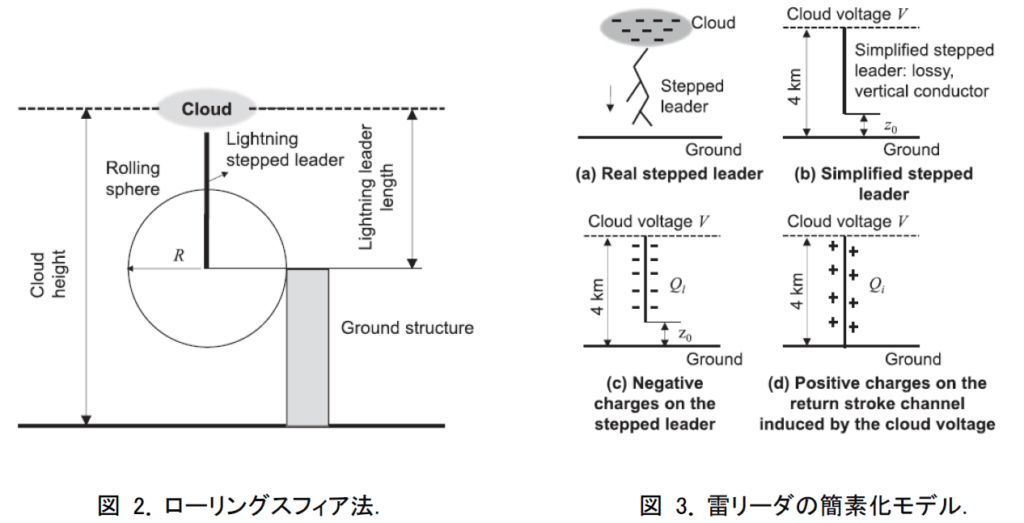
雷リーダが地面に近づくに達するとき、リーダの電荷密度は雲の帯電による電界と地上構造 物からの電界増強の両方に依存する。ここでは、図圠示した簡素化モデルを採用する。雷リー ダに沿った電流分布 $\lambda $は式(2)に表される ${ }^{2) }$。

$$
\lambda(\eta)=a_{0} \cdot\left(1-\frac{\eta}{H-z_{0}}\right) \cdot G\left(z_{0}\right) \cdot I_{\text {peak }}+\frac{I_{\text {peak }} \cdot(a+b \cdot \eta)}{1+c \cdot \eta+d \cdot \eta^{2}} \cdot F\left(z_{0}\right), \quad 0 \leq \eta \leq L, \quad z_{0} \geq 10 \tag{2}
$$

ここで、 $\eta$ は雷リーダの先端からの距離 $(\mathrm{m}), \eta=z-z_{0}, H$ は雲の高さ、 $z_{0}$ は地表面と雷リーダの 先端の距離 $(\mathrm{m}), I_{\text {peak }}$ は帰還雷撃のピーク電流 $(\mathrm{kA})$ であり、

$$
\begin{aligned}
& G\left(z_{0}\right)=1-\left(z_{0} / H\right), \\
& F\left(z_{0}\right)=0.3 \alpha+0.7 \beta, \alpha=e^{-\left(z_{0}-10\right) / 75}, \beta=1-\left(z_{0} / H\right) \\
& a_{0}=1.476 \cdot 10^{-5}, \\
& a=4.857 \cdot 10^{-5}, b=3.9097 \cdot 10^{-6}, c=0.522, d=3.73 \cdot 10^{-3}
\end{aligned}
$$

である。

高圧架空電線路は長距離にわたって自然の厳しい条件にさらされるため、雷撃を受ける機会も多く. 高圧架空電線路の体単体の研究3が行われたが、雷放電は自然界に存在する $\mathrm{km}$ に及ぶ超長ギャップ放電であり、その形態は、数センチ程度のギャップ長の実験室放電とは大きく異なる。図4に送電線路を示している。複合絶縁体（碍子）が送電線路における鉄塔に実装されるため、複合絶縁体の絶縁評価は広い空間における $3 \mathrm{D}$ 解析が必要であると考えられる。そこで本例題は、COMSOL Multiphysicsを用いて雷リーダによる高圧架空電線路における複合絶縁体（碍子）の3D電界分布を解析した。解析モデルは図5に示す。

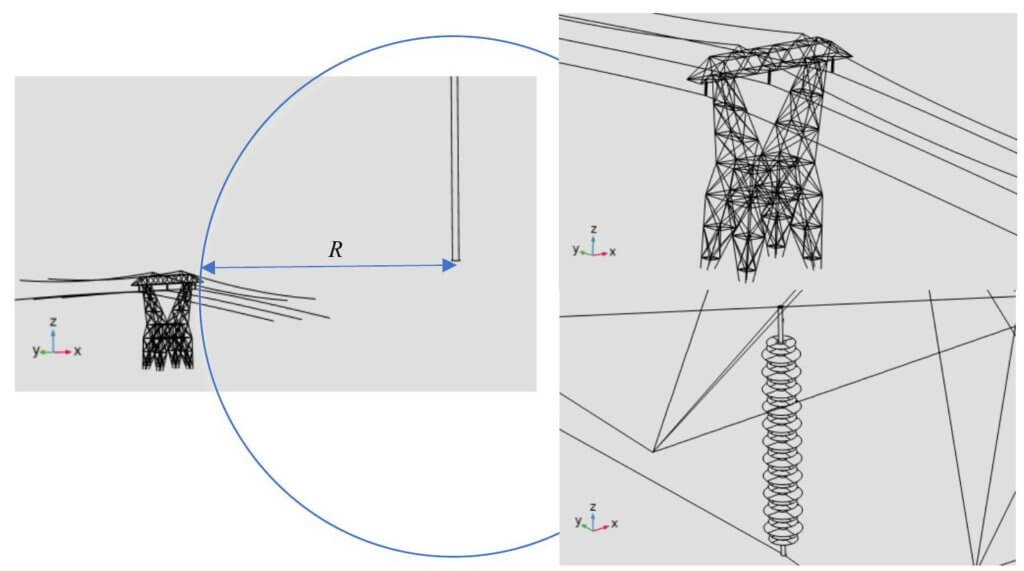
本書では、モデルおよび、2章以後に図 6 の解析結果を作成する手順を示す。

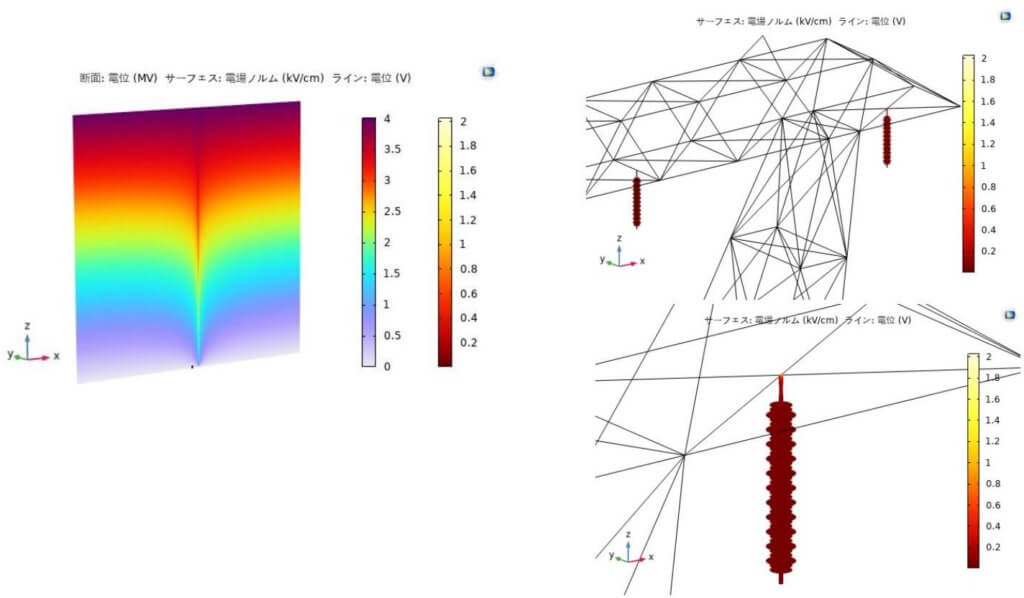
図 6 に第一帰還雷撃のピーク電流を $100 \mathrm{kA}$ とした雷リーダによる電界分布の計算結果を示している。雲層の電圧は $4 \mathrm{MV}$ 、計算領域は $4 \mathrm{~km} \times 4 \mathrm{~km} \times 4 \mathrm{~km}$ とした。雷りーダの速度 $V_{l}$ と半径 $R_{l}$ は それぞれ $10^{5} \mathrm{~m} / \mathrm{s}$ と $1.5 \mathrm{~m}$ を設定した。それによって、式(2)に示した電流密度 $\lambda(\eta)$ をCOMSOL設定パラメータである空間電荷密度 $\rho(\eta)$ に切り替え、以下に書き換えられた。

$$
\rho(\eta)=\lambda(\eta) /\left(\pi R_{l}{ }^{2}\right) / V_{l} \tag{3}
$$

図 6 に示したように複合絶縁体の芯棒の上部に最大電場が示され、 $2 \mathrm{kV} / \mathrm{cm}$ があった。水滴が付着した高圧絶縁体表面にコロナを発生させる電場は $10 \mathrm{kV} / \mathrm{cm}$ 以下であり、最小限のコロナを確保するための最大許容電場は $4.2 \mathrm{kV} / \mathrm{cm}$ であることが既に報告された ${ }^{4) 5) }$. 従って、雷リーダに対して現在の複合絶緑体（碍子）の絶縁性が十分であると示唆している。

参考文献

1) 牛尾知雄, 日本物理学会誌, Vol. 71, No. 4, 2016: 235-238.
2) Y. Wang and O. I. Zhupanska, Wind Energ., Vol. 20, 2017: 927-942.
3) X. Zhao, X. Yang, J. Hu, et al., IEEE Trans. Dielectr. Electr. Insul., Vol. 26, No. 4, 2019: 1253-1259
4) A.J. Phillips, D.J. Childs, and H.M. Schneider, IEEE Trans. Power Del., vol. 14, No. 3, 1999: 10811089.
5) K. Eleperuma, T. P. Saha, and T. Gillespie, Aust. J. Electr. Electron. Eng., Vol. 4, No.3, 2008: 239-248.

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。