リチウムイオン二次電池は、車両分野・通信分野・産業分野・建設分野・再生可能エネルギー・携帯機器と、幅広い分野で活用されており、現代の生活には欠かせないものとなっている。リチウムイオン二次電池は、充放電の繰り返しで劣化する。使用環境条件によっては、想定した設計サイクル寿命を待たずに機能を停止し、事故に繋がることがある。
交流インピーダンス測定法は、試料電池へ微少な交流電流を流して、基準交流波と比較することで、試料電池のインピーダンスを複素インピーダンス（インピーダンスの大きさと位相）として求める方法である。交流の周波数を少しずつ変化させ、各周波数で得られるインピーダンスと位相差を複素平面上にプロットすることで電池の内部インピーダンスを視覚的に明確化できる。ここでは、リチウムイオン二次電池の容量を減少させる要因として、負極表面に SEI（Solid Electrolyte Interphase）層を生成するモデルを構築し、充放電サイクルによる劣化の進展に着目してリチウムイオン二次電池のインピーダンス解析を行う。充放電サイクル、劣化およびインピーダンス計算のモデリング手法を示す。

SEIを生成する寄生的なリチウムイオンの還元反応は式(1)に示されている ${ }^{1)}$。

$$
\mathrm{S}+\mathrm{Li}^{+}+e^{-}=\mathrm{P}_{\mathrm{SEI}} \tag{1}
$$

ここで、 $\mathrm{S}$ は溶媒、$\mathrm{P}_{\mathrm{SEI}}$ は生成物である。 $\mathrm{P}_{\mathrm{SEI}}$ が生成されると、バッテリー内のリサイクル可能なリチウムが失われ、SEI層の抵抗の増加および負極における電解液の体積分率の減少をさせる。低から中程度の充放電レートであれば、 $\mathrm{Li}^{+}$濃度および溶媒濃度は過剩に存在するため、溶液中の $\mathrm{Li}^{+}$の濃度が大きく変化しないと想定できる ${ }^{1)}$ 。これに基づいて、この寄生反応は濃度依存性を考慮しない陰極ターフェル反応速度論に従う ${ }^{1)2)}$。

$$
i_{\text {para }}=-i_{\text {para }, 0} \exp \left(\frac{-\alpha_{c} F \eta}{R T}\right) \tag{2}
$$

ここで、 $i_{\mathrm{para}}$ は寄生反応電流密度、 $i_{\mathrm{para}, 0}$ は交換電流密度、 $\alpha_{c}$ はカソードの電荷移動係数、 $F$ はフ アラデー定数、$\eta$ は過電圧、 $R$ は気体定数、 $T$ は温度である。
交流インピーダンスZ்は、複素数で表され、実部と虚部をされぞれ $Z_{\mathrm{Re}}$ と $Z_{\mathrm{lm}}$ で表すと、虚数単位をjとして次式に書ける。

$$
\dot{Z}=Z_{\mathrm{Re}}-j Z_{\mathrm{lm}} \tag{3}
$$

ベクトルZ்の大きさ $|\dot{Z}|$ と位相角 $\phi$ は次の内容をもつ。

$$
|\dot{Z}|=\sqrt{Z_{\mathrm{Re}}^{2}+Z_{\mathrm{lm}}{ }^{2}} \tag{4}
$$

$$
\tan \phi=\frac{Z_{\mathrm{lm}}}{Z_{\mathrm{Re}}} \tag{5}
$$

この計算例は、COMSOL Multiphysics を用いて、交流インピーダンス測定法と同じ手法で微少な交流信号を流してリチウムイオン二次電池のインピーダンスを考察する。図1 にリチウムイオン二次電池モデルを示す。正極を$\mathrm{NCA}\left(\mathrm{LiNi}{0.8} \mathrm{Co}{0.15} \mathrm{Al}{0.05} \mathrm{O}{2}\right)$ 、負極をグラファイト(黒鉛)、電解液を $\mathrm{LiPF}_{6} / \mathrm{EC}: \mathrm{EMC}$ (3:7)とするリチウムイオン電池の $1 \mathrm{D}$ モデルが利用される。

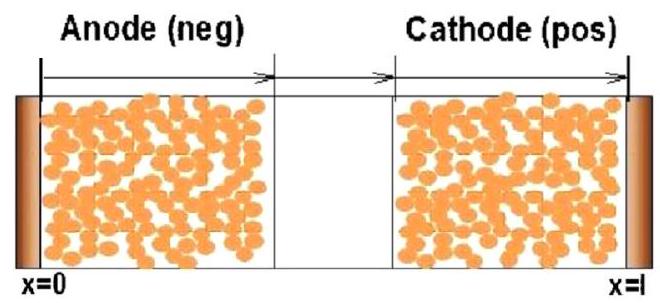
リチウムイオン電池の解析は、電極活物質内の $\mathrm{Li}$ が固液界面における挿入・脱離反応および電解液中の $\mathrm{Li}^{+}$が泳動・拡散を通して、対極の活物質へ輸送される計算を行う。電池の充放電過程に対する電極で起こる電気化学反応は Butler-Volmer 式でモデル化される ${ }^{3)}$。

$$
i_{\mathrm{loc}}=i_{0}\left[\exp \left(\frac{\alpha_{a} F \eta}{R T}\right)-\exp \left(\frac{-\alpha_{c} F \eta}{R T}\right)\right] \tag{6}
$$

$$
i_{0}=i_{0, \text { ref }}(T)\left(\frac{c_{s}}{c_{s, \text { ref }}}\right)^{\alpha_{c}}\left(\frac{c_{s, \text { max }}-c_{s}}{c_{s, \text { max }}-c_{s, \text { ref }}}\right)^{\alpha_{a}}\left(\frac{c_{l}}{c_{l, \text { ref }}}\right)^{\alpha_{a}} \tag{7}
$$

ここで、 $i_{\mathrm{loc}}$ は電極表面（活物質粒子表面）電流密度、 $\alpha_{a}$ と $\alpha_{c}$ は電荷移動係数、 $\eta$ は過電圧、 $i_{0}$ は交換電流密度、 $i_{0, \mathrm{ref}}$ は基準電位である交換電流密度、 $c_{l}$ と $c_{s}$ は電解質中の $\mathrm{Li}^{+}$濃度と電極内の $\mathrm{Li}$濃度、 $c_{l, \text { ref }}$ は電解質塩の参照濃度、 $c_{s, \max }$ は電極内 $\mathrm{Li}$ の最大濃度である。
多孔質電極における活物質粒子表面の $\mathrm{Li}$ 挿入反応は次式で表される。

$$
\mathrm{Li}^{+}+e^{-}+\Theta_{s} \Leftrightarrow \mathrm{Li}_{s} \tag{8}
$$

ここで、 $\Theta_{s}$ と $\mathrm{Li}_{s}$ はそれぞれ活物質粒子表面の空きサイトと埋まったサイトである。活物質粒子中の $\mathrm{Li}$ 輸送計算は、電池の空間次元の上に追加次元1Dで行われる。

$$
\frac{\partial c_{s}}{\partial t}=-\nabla \cdot\left(-D_{\mathrm{s}} \nabla c_{\mathrm{s}}\right) \tag{9}
$$

式(9)の境界条件は以下に定義される。

$$
\left.\frac{\partial c_{s}}{\partial r}\right|{r=0}=0, \quad-\left.D{s} \frac{\partial c_{s}}{\partial r}\right|{r=1}=-R_{\mathrm{Li} \Theta}
$$

ここで、 $D_{\mathrm{s}}$ は $\mathrm{Li}$ の拡散係数、 $R_{\mathrm{Li} \Theta}$ は $\mathrm{Li}$ のル流束、 $r$ は追加次元 $1 \mathrm{D}$ の正規化された座標である。 $r=0$ は活物質粒子中心、 $r=1$ は活物質粒子表面と表される。

電解液における $\mathrm{Li}^{+}$輸送は高濃度電解液理論に従う ${ }^{3)}$。バイナリー電解質における $\mathrm{Li}^{+}+$輸送は次式で表される。

$$
\frac{\partial\left(\epsilon_{l} c_{l}\right)}{\partial t}+\nabla \cdot \mathbf{J}_{l}=R_{l} \tag{10}
$$

$$
\mathbf{J}_{l}=-D_{l, \mathrm{eff}} \nabla c_{l}+\frac{\mathbf{i}_{l} t_{+}}{F} \tag{11}
$$

ここで、 $\epsilon_{l}$ は電解質の占める体積率、 $\mathbf{J}{l}$ は $\mathrm{Li}^{+}$のフラックス, $D{l, \mathrm{eff}}$ は $\mathrm{Li}^{+}$の有効拡散係数、 $\mathbf{i}{l}$ は電解質の電流密度、 $t_{+}$は $\mathrm{Li}^{+}$の転送係数、$R_{l}$ はソース項である。
電解質および電極における電流分布 $\mathbf{i}{l}$ と $\mathbf{i}{s}$ は次式で表される。

$$
\nabla \cdot \mathbf{i}_{l}=i_{t o t}+Q_{l} \ \tag{12}
$$

$$
\nabla \cdot \mathbf{i}_{s}=-i_{t o t}+Q_{s} \tag{13}
$$

$$
\mathbf{i}{l}=-\sigma{l, \mathrm{eff}} \nabla \phi_{l}+\frac{2 \sigma_{l, \mathrm{eff}} R T}{F}\left(1+\frac{\partial \ln f}{\partial \ln c_{l}}\right)\left(1-t_{+}\right) \nabla \ln c_{l} \tag{14}
$$

$$
\mathbf{i}{s}=-\sigma{s, \mathrm{eff}} \nabla \phi_{s} \tag{15}
$$

ここで、$\phi_{l}$ と $\phi_{s}$ はそれぞれ電解質と電極の電位、$\sigma_{l, \mathrm{eff}}$ と $\sigma_{s, \mathrm{eff}}$ は電解質と電極の有効導電率、$i_{t o t}$ は電気化学反応の総電流密度、$f$ は活量係数、$Q_{l}$ と $Q_{S}$ はそれぞれ電解質と電極の電流ソース項である。
本書では解析モデルおよび，図 3 の解析結果を作成する手順を示した。

図 2 に示した COMSOL Multiphysics の溶解-沈着化学種のセクションで、SEI の密度およびモル質量を定義し、薄膜抵抗のセクションで、充放電サイクルによって SEI 厚みの計算パラメーターを設定する。

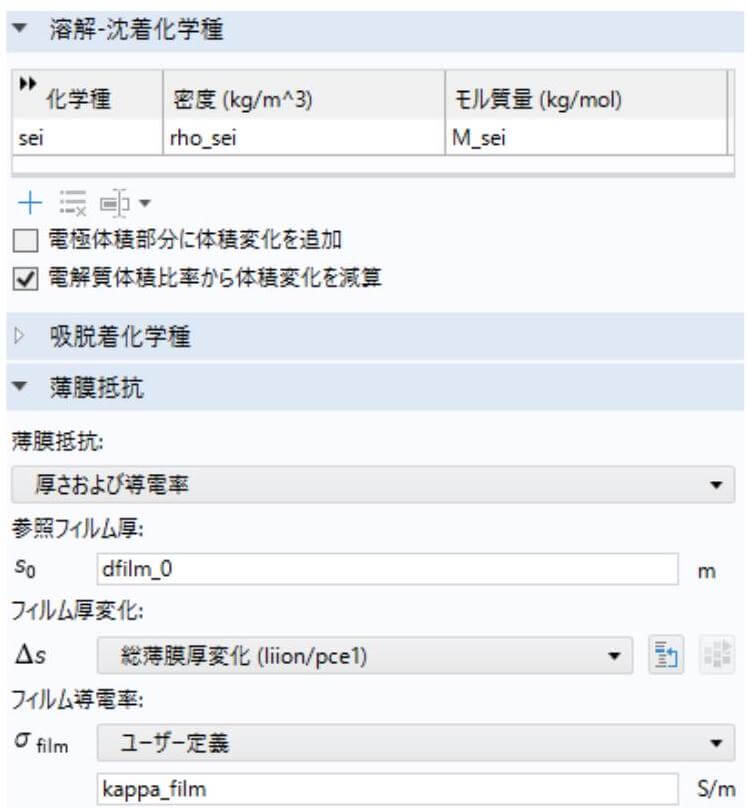
負極 (グラファイト)における SEI 種の濃度および SEI 層の厚みの計算式は次の内容をもつ。

$$
\frac{\partial c_{\mathrm{SEI}}}{\partial t}=-\frac{v_{\mathrm{SEI}} i_{\mathrm{para}}}{n F} \tag{16}
$$

$$
\delta_{\mathrm{film}}=-\frac{c_{\mathrm{SEI}} M_{\mathrm{SEI}}}{A_{v} \rho_{\mathrm{SEI}}} \tag{17}
$$

ここで、 $c_{\mathrm{SEI}}$ は $\mathrm{SEI}$ 種の濃度、 $v_{\mathrm{SEI}}$ は $\mathrm{SEI}$ 種の化学量論係数、 $\delta_{\mathrm{film}}$ は $\mathrm{SEI}$ 層の厚み、 $A_{v}$ は電極の活性化比表面積、 $M_{\mathrm{SEI}}$ と $\rho_{\mathrm{SEI}}$ はそれぞれ $\mathrm{SEI}$ 種のモル質量と密度である。
計算には1つの充放電シミュレーションサイクルで、より多くのサイクルにおける平均化した劣化挙動と表わされ、SEI層に捕捉されたリチウムが全て負極から出てくることをモデリングした。容量損失は、SEIを形成させる反応式(1)の化学量論係数を書き直して加速因子 $\tau$ を導入した。

$$
\tau \mathrm{S}+\mathrm{Li}^{+}+e^{-}+(\tau-1) \mathrm{Li}{s}=\tau \mathrm{P}_{\mathrm{SEI}} \tag{18}
$$

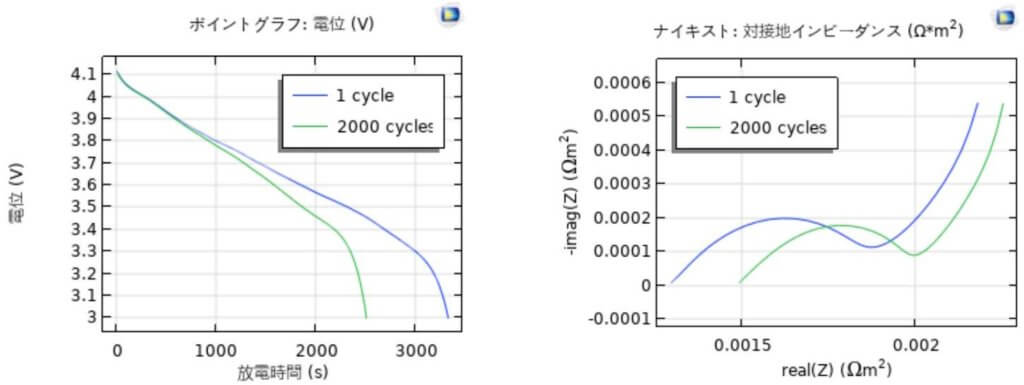
計算結果は図 3 に示している。加速因子 $\tau$ を250として、劣化を含む充放電サイクルを8回計算して、実際の充放電サイクルは2000になった。劣化になる前のリチウムイオン二次電池のインピーダンスと比較するため、劣化が発生する前に1つの充放電サイクルを計算した。リチウムイオン二次電池の放電曲線およびインピーダンスの計算結果を図3に示した。劣化によって、電池容量が減らすことが示された。インピーダンスの実部を増やしたが、インピーダンスの虚部は少し減少すると示唆される。これは、リチウムイオン挿入反応に対する電荷移動抵抗は式(7)に示した交換電流 $i_{0} $ に依存し、$c_{l}$ と $c_{s}$ の変化がバランスをとっていく結果であると考えられる。

参考文献

1) P. Ramadass, B. Haran, P. Gomadam, R. White, and B. N. Popov, “Development of first principles capacity fade model for li-ion cells,” J. Electrochemical Society, Vol. 151, No. 2, A196-A203 (2004).
2) G. Ning, R. E. White, and B. N. Popov, “A generalized cycle life model of rechargeable li-ion batteries”, Electrochimica Acta, Vol. 51, 2012-2022 (2006).
3) 佟立柱、福川真、リチウムイオン電池・全固体電池のシミュレーション技術－ Li イオンの輸送と反応に基づく電気化学モデルから集中パラメータによる電池モデルまでー、計算工学、 Vol. 25, No. 4, 4145-4150 (2020).

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。