円筒型、角型およびラミネート (パウチ) 型のリチウムイオン電池は、スマホバッテリーや電気自動車搭載電池、家庭用蓄電池など幅広い分野で応用されている。重量およびコストを削減しならびにパッケージング効率を高めたラミネート型リチウムイオン電池は、電気自動車などに搭載されることで注目されている。
電気自動車用のリチウムイオン電池は、HEV、BEV など様々な用途に対応する必要があり、エネルギー密度とパワー密度を用途に合わせて設計することになる、ラミネート型リチウムイオ ン電池(図 1)では、積層電極の面積と積層数によって容量が決まるため、設計の変更が比較的容易であり、外装にもラミネートフィルムを使用しているため容器としての自由度も高く、様々な用途へ対応することが可能な構造である。
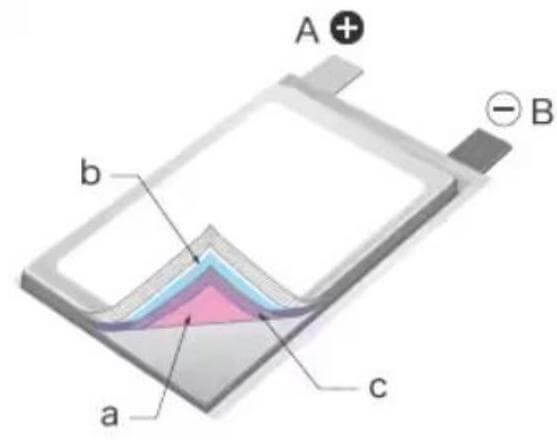
A : 正極端子 B:負極端子
a: 正極 b: 負極 c:セパレータ
図 1.ラミネート型リチウムイオン電池
ラミネート型リチウムイオン電池は、円筒形電池と比べて表面積が広いため放熱性が高く、充放電によるセル全体の温度上昇を低く抑えることが可能である。
この計算例は、COMSOL Multiphysics® を用いて、ラミネート型リチウムイオン電池の 3 次元シミュレーションを行う。電解質中のリチウムイオンの濃度分布と電流分布、電極内の充電率の変化および電池の放電特性を示し、電池の発熱挙動を考察する。
リチウムイオン電池における電解液中のリチウムイオン輸送は高濃度電解液理論に従う。これによって、リチウムイオン輸送への駆動力は電気化学ポテンシャル勾配で決められる ${ }^{1)}$。
$$
c_{i} \nabla \mu_{i}=\sum_{j \neq i} K_{i j}\left(\mathrm{v}{j}-\mathrm{v}{i}\right) \tag{1}
$$
ここで、$c_{i}$ は濃度、$\mu_{i}$ は電気化学ポテンシャル、$K_{i j}$ は交互作用係数、$\mathrm{v}{i}$ と $\mathrm{v}{j}$ は速度である。
バイナリー電解質においては、リチウムイオン輸送および電流分布が次式で求まる。
$$
\mathbf{N}{+}=-D_{l} \nabla c_{l}+\frac{\mathbf{i}_{l} t{+}}{F} \tag{2}
$$
$$
\mathbf{i}_{l}=-\sigma_{l} \nabla \phi_{l}+\frac{2 \sigma_{l} R T}{F}\left(1+\frac{\partial \ln f}{\partial \ln c_{l}}\right)\left(1-t_{+}\right) \nabla \ln c_{l} \tag{3}
$$
ここに、$\mathbf{N}{+}$は流量、$D{l}$ は拡散係数、$\mathbf{i}{l}$ は電解質の電流密度、$t{+}$は $\mathrm{Li}^{+}$の転送係数、$F$ はファラデー定数、$\phi_{l}$ は電解質の電位、$\sigma_{l}$ は電解質の導電率、$R$ は気体定数、$T$ は絶対温度、$f$ は電解質塩の活量係数である。
正極と負極にリチウムイオンを挿入・脱離する電気化学反応は次式で示される ${ }^{2,3)}$。
$$
\mathrm{Li}^{+}+e^{-}+\Theta_{s} \Leftrightarrow \mathrm{Li}\Theta_{s} \tag{4}
$$
ここに、$\Theta_{s}$ は自由な反応サイト、$\mathrm{Li}_{s}$ は占拠された反応サイトである。式(4)に対するバトラー・ ボルマー式は
$$
i_{l o c}=i_{0}\left[\exp \left(\frac{\alpha_{a} F \eta}{R T}\right)-\exp \left(\frac{-\alpha_{c} F \eta}{R T}\right)\right] \tag{5}
$$
$$
i_{0}=i_{0, \text { ref }}(T)\left(\frac{c_{s}}{c_{s, \text { ref }}}\right)^{\alpha_{c}}\left(\frac{c_{s, \text { max }}-c_{s}}{c_{s, \text { max }}-c_{s, \text { ref }}}\right)^{\alpha_{a}}\left(\frac{c_{l}}{c_{l, \text { ref }}}\right)^{\alpha_{a}} \tag{6}
$$
ここで、$i_{\mathrm{loc}}$ は電極表面(活物質粒子表面)電流密度、$\alpha_{a}$ と $\alpha_{c}$ は電荷移動係数、$\eta$ は過電圧、$i_{0}$ は交換電流密度、$i_{0, \text { ref }}$ は基準電位である交換電流密度、$c_{l}$ と $c_{s}$ は電解質中の $\mathrm{Li}^{+}$濃度と電極内の $\mathrm{Li}$ 濃度、$c_{l, \text { ref }}$ は電解質塩の参照濃度、$c_{s, \max }$ は電極内 $\mathrm{Li}$ の最大濃度である。
多孔質電極における活物質粒子中のリチウム種の輸送計算は、空間次元の上に追加次元 $1 \mathrm{D}$ で行われる。
$$
\frac{\partial c_{s}}{\partial t}=-\nabla \cdot\left(-D_{\mathrm{s}} \nabla c_{\mathrm{s}}\right) \tag{7}
$$
式(7)の境界条件は以下に定義される。
$$
\left.\frac{\partial c_{s}}{\partial r}\right|_{r=0}=0, \quad-\left.D{s} \frac{\partial c_{s}}{\partial r}\right|_{r=1}=-R_{\mathrm{Li \Theta}} \tag{8}
$$
ここで、$D_{\mathrm{s}}$ は $\mathrm{Li}$ の拡散係数、$R_{\mathrm{Li \Theta}}$ は $\mathrm{Li}$ のモル流束、 $r$ は追加次元 $1 \mathrm{D}$ の正規化された座標である. $r=0$ は活物質粒子中心、 $r=1$ は活物質粒子表面と表される。
リチウムイオン電池におけるオーム損失、電気化学反応および反応混合物による発熱が生じる熱伝導現象は次式でモデル化される。
$$
\rho C_{p} \frac{\partial T}{\partial t}+\nabla \cdot \mathbf{q}=Q_{j h}+Q_{c h e m}+Q_{m} \tag{9}
$$
ここで、$T$ は温度、$\rho$ は密度、$C_{p}$ は熱容量である、q は熱流束、$\mathbf{q}=-k \nabla T$ と定義される。ここに、$k$ は熱伝導度である。$Q_{j h}, Q_{c h e m}$ および $Q_{m}$ はそれぞれオーム損失、電気化学反応および反応混合物による発熱項である。
本書では解析モデルおよび、図 2 の解析結果を作成する手順を示した。
解析モデルは図 1 に示したように、正極を $\mathrm{NMC}\left(\mathrm{LiNi}{1 / 3} \mathrm{Mn}{1 / 3} \mathrm{Co}{1 / 3} \mathrm{O}{2}\right)$、負極をグラファイト (黒鉛)、電解液を $\mathrm{LiPF}_{6} / \mathrm{EC}: \mathrm{DEC}(1: 1)$ とする幅 $12.5 \mathrm{~cm}$、長さ $19.5 \mathrm{~cm}$、厚さ $0.019 \mathrm{~cm}$ であるラミネ 一ト型セル${ }^{4)}$をモデル化した。セルの中心には、セパレータ $(25 \mu \mathrm{m})$ があり、その両側は負極と正極 (それぞれ $79 \mu \mathrm{m}$ と $70 \mu \mathrm{m}$ )、負極と正極の外側は電流コレクタ(それぞれ $12 \mu \mathrm{m}$ と $21 \mu \mathrm{m}$ )がある。タブは電流コレクタの同じ厚さであり、負極と正極の電流コレクタの同一端に付る。セル電圧を 1 と $4 \mathrm{C}$ レートで $3 \mathrm{~V}$ まで放電する計算を行った。 計算時間は 44 分 21 秒でした。 計算用のパソコンスペックは以下の通りで
- OS: Windows 10 Pro
- プロセッサ: Intel(R) Xeon(R) Gold 6334 CPU @ 3.60GHz 3.70 GHz
- 実装 RAM 128 GB
ある。計算結果は図 2 に示している。結果を明確的に示すため、セルの厚さを 150 倍に拡大して 表示された。1Cレートで放電完了の時の電解質電位と電流密度、電解質塩の濃度、および電極 の充電状態(SOC)を示している。1 と 4 C レートでの放電曲線および放電完了の時の温度分布 も示された。放電完了の時にタブ端子の反対側に高い温度が形成され、温度分布の不均一性が明らかになった。
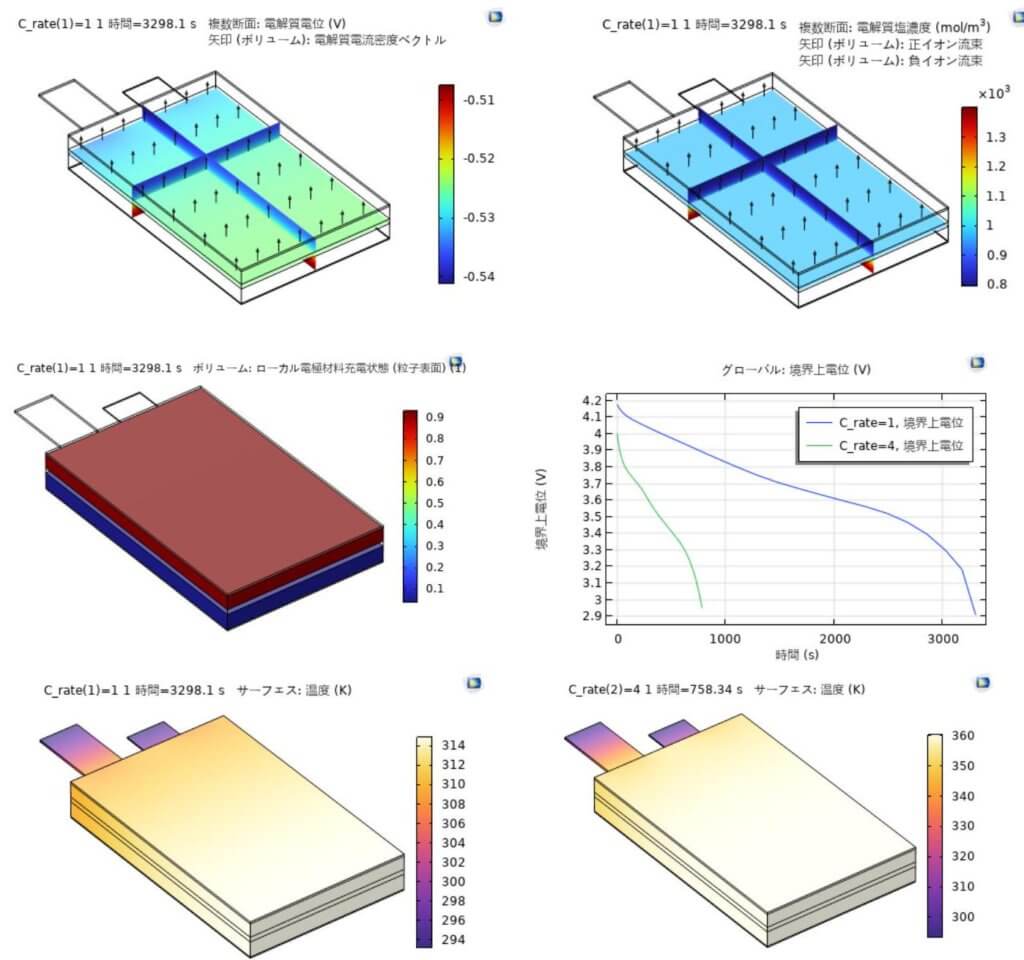
図 2. ラミネート型リチウムイオン電池の計算結果.
参考文献
1) Newman, J. and Thomas Alyea, K. E., Electrochemical Systems , 3rd ed., John Wiley & Sons, Hoboken
NJ (2004) 2004).
2) Thomas, K. E., Darling, R. M., and Newman, J., Mathematical Modeling of Lithium Batteries , in
Advances in Lithium Ion Batteries , Van Schalkwijk, W. A. and Scrosati, B., Editors, Kluwer
Academic/Plenum Publishers, New York, (2002), pp.345 392392.
3) 佟立柱、福川真、リチウムイオン電池・全固体電池のシミュレーション技術- Li イオンの輸送と反応に基づく電気化学モデルから集中パラメータによる電池モデルまで-、計算工学、Vol. 25, No. 4, 4145 4150 (2020).
4) Yazdanpour, M., Taheri, P., Mansouri, A., and Bahrami, M., A Distributed Analytical Electro Thermal
Model for Pouch Type Lithium Ion Batteries, Journal of The Electrochemical Society , Vol. 161, No.
14 (2014), pp. A1953 A1963.
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。