水溶液を用いて金属を電気化学的に還元析出する電析プロセスは、金属の分離、回収、精製を目的とした電解精製工程や電解採取工程、素材の表面処理や電子デバイスの配線形成における めっきプロセスなどの幅広い用途で用いられる重要な技術である。
電析プロセスにおける電流分布は電気化学セルの動作を特徴付ける重要なパラメーターである。高品質めっき加工には作用電極上の均一な電流分布が必要で、電流密度条件を改善することが要求されている。
回転形ハルセル(Rotating Cylinder Hull、RCH) ${ }^{1)}$ は、外側絶縁チューブと同軸の内側円筒電極で構成される。この構造において、均一な物質移動分布があり、その大きさを簡単に変更できる。回転形ハルセルを用いて、電流分布と物質移動効果を同時に含むプロセスを検討できる。図 1 に回転電極および回転形ハルセル $(\mathrm{RCH})$ の構造を示す。

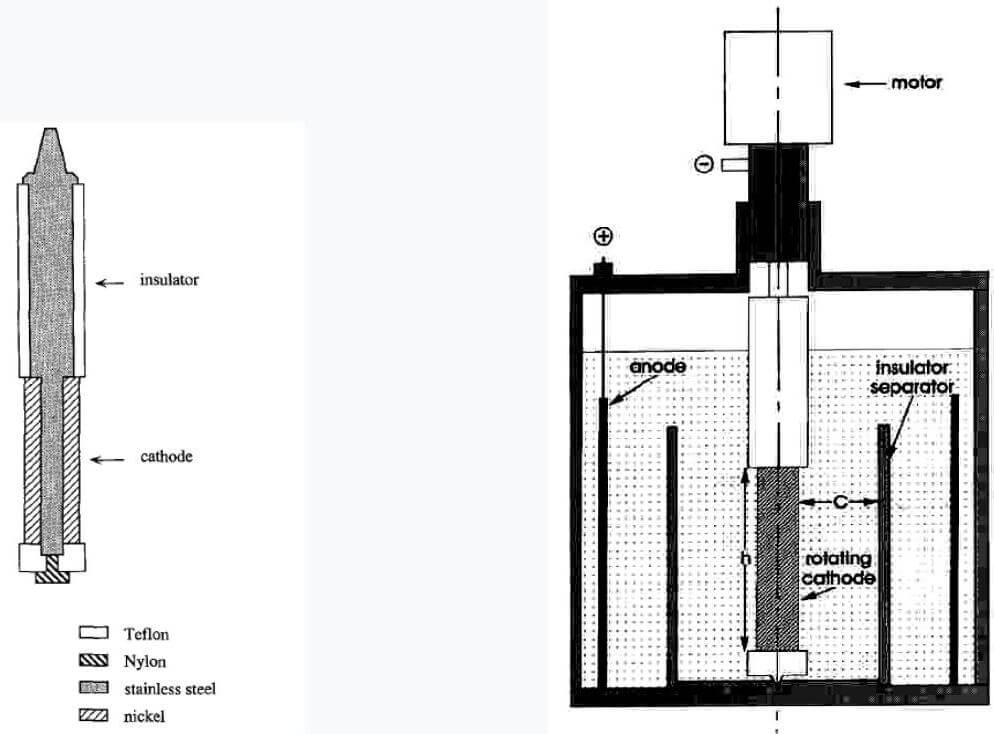
図 1. 回転電極および回転形ハルセル $(\mathrm{RCH})$ の構造 ${ }^{1,2)}$。

電気化学反応器の設計では、寸法一貫性とした電気の類似性についてスケールアップ基準が必要である。無次元のワグナー数 (以下 $W a_{\mathrm{T}}$ 数) は、電流分布に対する過電位の影響を特徴付ける量として使用される。この $W a_{\mathrm{T}}$ 数は、スケールアップ設計における均一な電流分布のガイドとして使用できる。ここでは、カソード表面の電極反応をターフェル式で表し、二次電流分布の均一性は次の形式の無次元 $W a_{\mathrm{T}}$ 数で表示される。

$$
W a_{\mathrm{T}}=\frac{\beta_{c} \kappa}{\left|i_{\mathrm{avg}}\right| h} \tag{1}
$$

ここで、$\kappa$ は電解液の導電率、$\beta_{c}$ はカソード反応のターフェル勾配、$i_{\mathrm{avg}}$ はカソード表面の平均電流密度、$h$ は電極システムの特徴的な長さ、ここではカソードの長さに等しいとする。

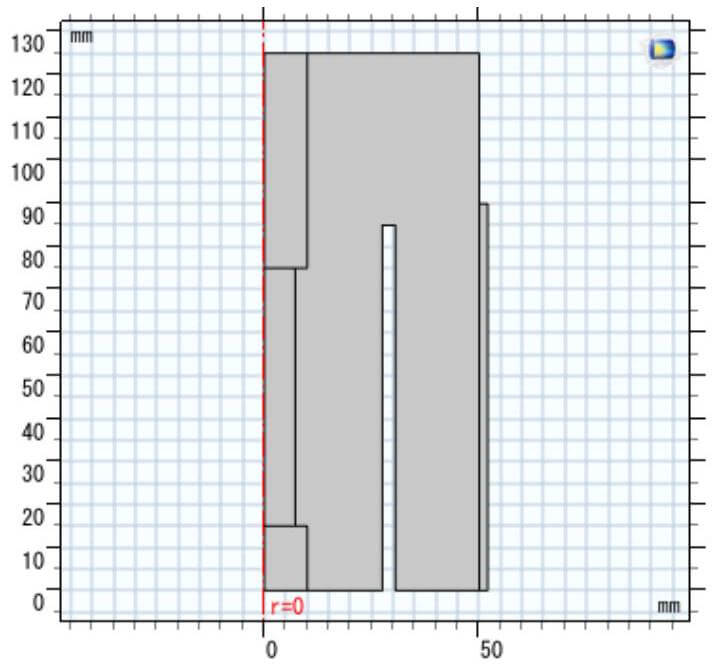
図 2. 解析モデル.

解析モデルを図 2 に示す。図 1 に示した回転形ハルセル $(\mathrm{RCH})$ と同じ構造で解析領域を液面とアノード表面までの溶液の領域とした。
本書では解析モデルおよび、図 3 の解析結果を作成する手順を示した。

モデルは軸対称 $2 \mathrm{D}$ で、電解質を、導電率 $0.35 \mathrm{~S} / \mathrm{cm}$ の硫酸銅水溶液であると想定する。式(1)によって、$W a_{\mathrm{T}}$数を0.03と１に対する平均電流密度をカソード表面に印加し、2次電流分布を計算する。
電解液の電位および電流密度をオームの法則によって求める。

$$
i=-\kappa \nabla \Phi \tag{2}
$$

$$
\nabla^{2} \Phi=0 \tag{3}
$$

アノードの電位を0とし、カソード表面の境界条件は電極反応速度論に基づく。

$$
-\kappa \partial \Phi / \partial n=i_{\mathrm{loc}} \tag{4}
$$

ここで、$i_{\text {loc }}$ はカソード表面電流密度で、ターフェル式で表される。

$$
i_{\text {loc }}=-i_{0} \exp \left(-\eta / \beta_{\mathrm{c}}\right) \tag{5}
$$

ここで、$i_{0}$ は交換電流密度、$\eta$ は過電圧である。$\eta=V_{\mathrm{c}}-\Phi-E_{\mathrm{eq}}、\quad V_{\mathrm{c}}$ はカソードの電位、$E_{\mathrm{eq}}$ は平衡電位である。ここでは、ターフェル勾配 $\beta_{c}=45 \mathrm{mV}$ と $E_{\mathrm{eq}}=0$ とする ${ }^{1)}$。それ以外の境界は絶縁とした。

図 3 に電解質電位およびカソード表面の電流分布を示している。めっき加工におけるめっき膜厚の均一性については、式(1)の $W a_{\mathrm{T}}$ 数で解釈することができ、膜厚均一性を良くするために $W a_{\mathrm{T}}$ 数を大きくすることは図 $3(\mathrm{~b})$ に示された。カソード表面の電流分布はシンボル表示とした文献１)からの測定値と一致することで、大きい $W a_{\mathrm{T}}$ 数があったカソード表面の電流分布は均一性が良くなる傾向が検証された。

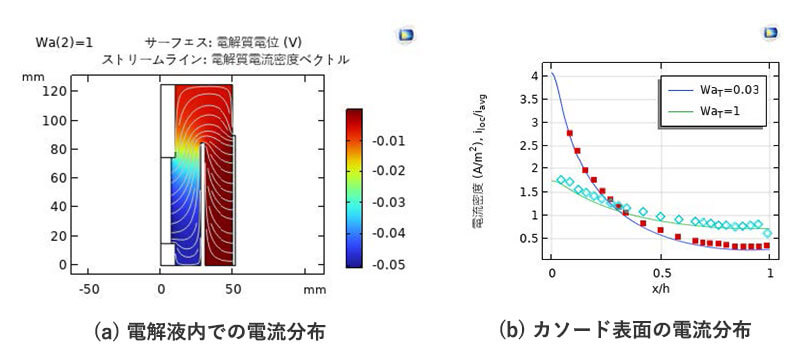
図 3. 回転形ハルセル $(\mathrm{RCH})$ の計算結果.

参考文献

1) Madore, C., Matlosz, M., and Landolt, D.: Experimental investigation of the primary and secondary
current distribution in a rotating cylinder Hull cell. J. Appl. Electrochem. 22, 1155–1160 (1992).
2) Madore, C., Landolt, D., Haenpflug, C., and Hermann, J.A.: Application of the rotating cylinder hull cell
to the measurement of throwing power & the monitoring of copper plating baths. Plating Surf. Finish. 82 (8), 36-41
(1995).

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。