バッテリーの安全性シミュレーション技術により、現象の把握、設計・評価の効率化へ寄与を目指している。熱暴走とは、電池セル内で連鎖的に起こる、電池の急激な温度上昇を伴う反応のことである。図1に $\mathrm{Li}(\mathrm{NiCoMn}) \mathrm{O}_{2}(\mathrm{NCM})$ 正極を備えた $25 \mathrm{Ah}$ 大型角形リチウムイオン電池の熱暴走の試験結果を示す。

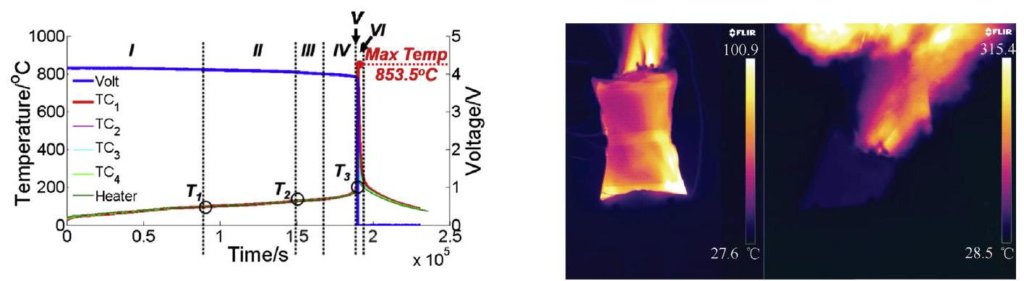
図 1. T,V)-t曲線およびサーモグラフィ画像 ${ }^{1)}$ .

熱暴走したセルからの延焼によって他のセルが次々と熱暴走すると、バッテリーパックの安全性や電気自動車の走行に大きな脅威となる。ここでは、これらの現象を予測することで、モジュールの安全設計に有用な情報を得る。
熱暴走中に放出されるエネルギーは、活物質と電解質の間の分解反応によって引き起こされる発熱反応によるものであることが一般的に認められる。これは通常の充放電時の電池の発熱と違っているため、モデリングの複雑性が非常に高くなると考えられる。また、深刻な熱暴走現象に耐えられるバッテリーパックを設計する場合、さまざまな化学反応を含む実際のセルに基づいた現実的な最悪のケースを想定したシナリオを描く必要である。これにより、熱暴走を考慮するため、発熱プロファイルまたは関数を定義する手法がある ${ }^{2)}$ 。ここでは、図 2 に示した発熱ファイルを採用した。

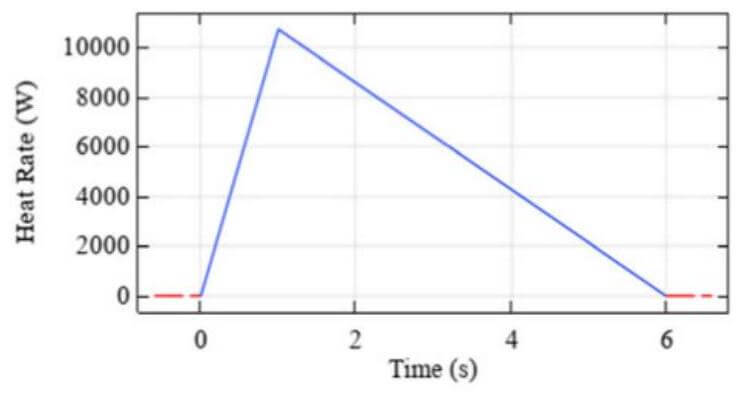
図 2. 熱暴走トリガー時の熱源 ${ }^{2)}$ .

この計算例は、電池セルにおけるオーム抵抗と電荷移動および拡散プロセスに基づく電池のすべての電圧損失を取り扱えるCOMSOL Multiphysics® ${ }^{\circledR}$ の集中電池モデル ${ }^{3)}$ と環境空気の熱流体挙動を連成計算し、バッテリーパックの熱暴走現象を考察する。
本書では解析モデルおよび、図 4 の解析結果を作成する手順を示した。

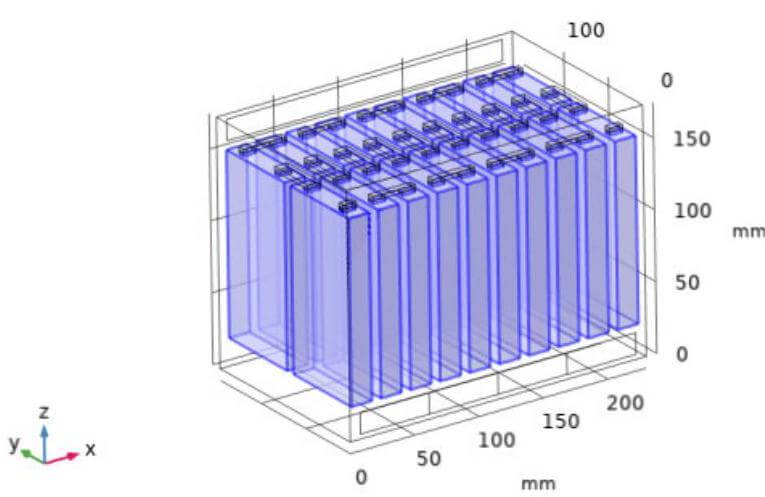
図 3. 解析モデル ${ }^{4)}$.

計算ジオメトリは、図 3 に示すような、容量 $2.5 \mathrm{Ah}$ の角形リチウムイオン電池 20 個からなるバッテリーパック ${ }^{4)}$ である。バッテリーは 10 直列 2 並列構成で接続される。電池の電圧 $E_{\mathrm{cell}}$ は次式で定義される。

$E_{\text {cell }}=E_{\mathrm{OCV}}(\mathrm{SOC}, T)+\eta_{\mathrm{IR}}+\eta_{\text {act }}+\eta_{\text {conc }}$

ここで、$E_{\mathrm{OCV}}(\mathrm{SOC}, T)$ は充電状態 (State Of Charge, $\mathrm{SOC}$ )に関する開回路電圧 (Open Circuit Voltage, $\mathrm{OCV}), T$ は温度、$\eta_{\mathrm{IR}}, \eta_{\mathrm{act}}$ および $\eta_{\mathrm{conc}}$ はそれぞれ抵抗分極、活性化分極および濃度分極である。

SOC は 1Dでの無次元変数 $X$ を用いて次式により得られる。

$$
\tau \frac{\partial \mathrm{SOC}}{\partial t}=-\nabla \cdot(-\nabla \mathrm{SOC})
$$

$\boldsymbol{\tau}$ は拡散時間定数、$t$ は時間である。境界条件は

$$
\begin{aligned}
-\left.\nabla \mathrm{SOC}\right|_{X=0} & =0 \\ -\left.\nabla \mathrm{SOC}\right|_{X=1} & =\frac{\tau I_{\text {cell }}}{N_{\text {shape }} Q_{\text {cell }}}
\end{aligned}
$$

となる。$X=0$ は粒子の中心、$X=1$ は粒子の表面と定義される。$N_{\text {shape }}$ は粒子の形状係数、1 はデカルト座標系、2 は円筒座標系、3 は球面座標系を意味する。リチウムイオンイオンバッテリーパックにおける熱暴走現象は以下の熱伝導方程式で計算される。

$$
\rho C_{p} \frac{\partial T}{\partial t}+\nabla \cdot \mathbf{q}=Q_{\mathrm{h}}
$$

ここで、$T$ は温度、$\rho$ は密度、$C_{p}$ は熱容量、$\mathbf{q}$ は熱流束、$Q_{\mathrm{h}}$ は熱源である。$\mathbf{q}=-k \nabla T$ と定義され、$k$ は熱伝導度である。
熱暴走の伝播を開始するには、充電サイクルの初期段階で 1 ケのセルが内部短絡などにより誤動作し始めると想定される。故障したセルのトリガーには図 2 に示した熱源 ${ }^{3) を}$ を利用する。他のセルについては、最高温度 $65^{\circ} \mathrm{C}$ に達すると、この熱源がトリガーされると考慮する。
図 4 は熱暴走がトリガーされた時と拡大した後のバッテリーパックの熱暴走伝播の計算結果である。熱暴走がトリガーされたセルから周辺に拡散することによって、空気の循環を計算して熱暴走伝播を解析した。

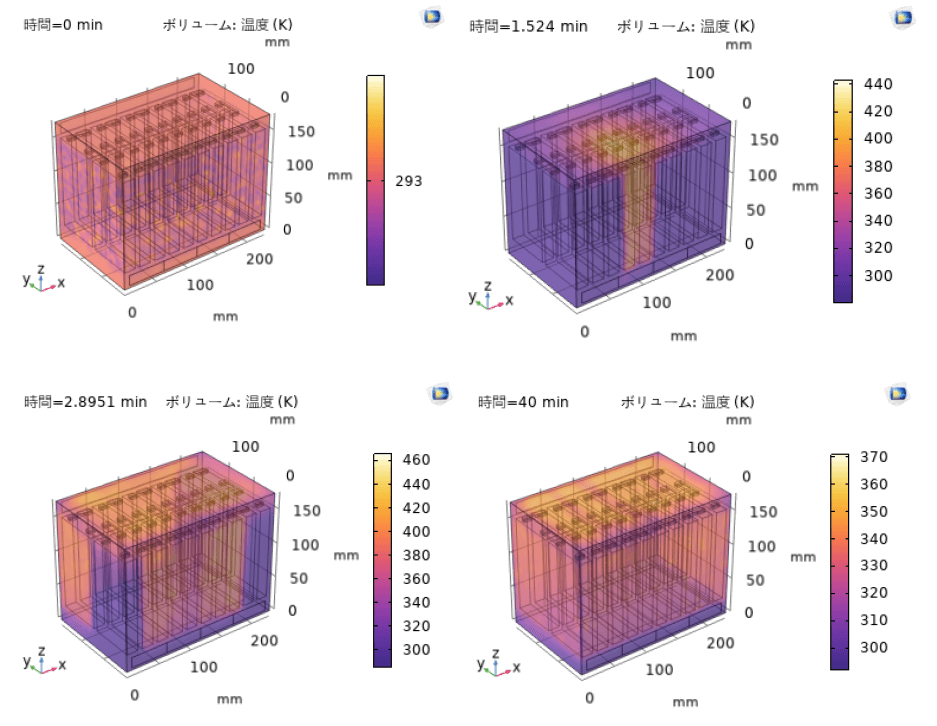
図 4. バッテリーパック内における熱暴走伝播

参考文献

1) X. Feng, M. Fang, X. He, et al., J. Power Sources 255, 294-301 (2014).
2) P.T. Coman, E.C. Darcy, and R.E. White, J. Electrochem. Soc. 169, 040516 (2022).
3) 佟立柱, 福川真, 計算工学 25(4), 4145-4150 (2020).
4) O. Yetik, N. Yilmaz, T.H. Karakoc, Int. J. Energy Res. 45, 13851-13864 (2021).

＊該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。