〜上村⼯業株式会社 (C. Uyemura & Co., Ltd.) ⽣本雷平様ご提供〜
半導体の微細化技術の進展によって、チップの高集積化、高速化、低消費電力化が年々進んでおり、電子機器の小型化・高機能化や高性能化を牽引する大きな推進力となっている。よって、高集積化、高速化されたチップの特性を引き出すためには配線密度が高い基板が必要となっている、微細配線パターンを有する基板では、パターン形状のサイズが $10 \mu \mathrm{m}$ のオーダーであり、基板サイズは100~300 mm(直径)のオーダーなので、パターン形状をそのまま再現するメッシユを基板全体に生成すると解析規模が膨大になり、計算が実現不可能である。この問題を解決するため、ここでは、図1に示したMehdizadehら${ }^{1)}$が提案したパターン率(めっき部の全面積に対する割合)を取り扱う。
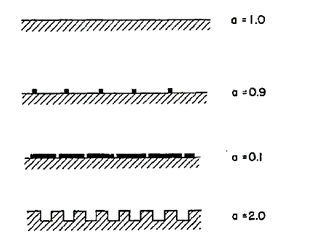
パターン率は単位表面積当たりのめっきする部分の面積を意味する。式(1)で定義される${ }^{1)}$。
$$
\begin{equation} a=\frac{A_{\text {ACT }}}{A_{\text {SUP }}} \tag{1} \end{equation}
$$
ここで、$a$ はパターン率、$A_{\mathrm{ACT}}$ はめっきする部分の面積、$A_{\mathrm{SUP}}$ は表面積 (superficial area, 平らな電極上の投影面積)である。
式(1)によって、パターン形状の影響をカソードとした基板表面の電流密度の計算に合わせる。カソード表面電流密度が式(2)で表示される。
$$
\begin{equation} \frac{-\kappa}{a i_{0}} \nabla \phi \cdot \mathbf{n}=e^{\frac{\alpha_{a} F \eta}{R T}}-e^{-\frac{\alpha_{c} F \eta}{R T}} \tag{2} \end{equation}
$$
ここで、 $\phi$ は電位、кはめっき液の電気伝導率、 $i_{0}$ は交換電流密度、 $\alpha_{a}$ と $\alpha_{c}$ はアノードとカソードの電荷交換係数、Fはファラデー定数、 $T$ は絶対温度、 $R$ は気体定数、 $\eta$ は過電圧である。
電気化学反応器の設計では、寸法一貫性とした電気の類似性についてスケールアップ基準が必要である。無次元のワグナー数 (以下 $W a$ 数) は、電流分布に対する過電位の影響を特徴付ける量として使用される。この $W a$ 数は、スケールアップ設計における均一な電流分布のガイドとして使用できる。ここでは、カソード表面にバトラー・ボルマー動力学のターフェル式を考慮し、二次電流分布の均一性は次の形式の無次元 $W a_{\mathrm{T}}$ 数で表示される ${ }^{1)}$。
$$
\begin{equation} W a_{\mathrm{T}}=\frac{R T \kappa}{\alpha_{\mathrm{C}} F L \bar{\tau}_{\mathrm{SUP}}} \tag{3} \end{equation}
$$
ここで、 $\bar{\imath}_{\text {SUP }}$ は表面積電流密度の平均値、$L$ は電極システムの特徴的な長さ、ここでは図 2 に示されている。
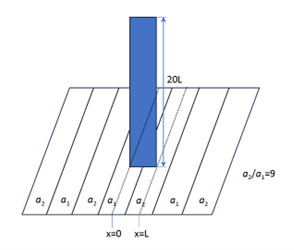
解析モデルを図 2 に示す。2Dモデルである。本例題は、異なるパターン率を持つ2つの領域が隣接した基本的なめっき問題を考慮する。無限に交互に繰り返される2つのパターン内での単一の対称部分のみとする。青色の矩形はめっき槽の単一の対称要素の2次元断面を示している。カソードの一部はパターン率 $a_{1}$ で、もう一部はパターン率 $a_{2}$ でパターン化される。 $\lambda$ は対称部分内におけるパターン率 $a_{1}$ 領域の幅を示す。パターン率の空間分布を $a^{*}$ として、次式で表示される${ }^{1)}$ 。
$$
\begin{equation} a^{*}=\frac{a_{1}}{\bar{a}}, \quad 0<x / L<\lambda \tag{4a} \end{equation}
$$
$$
\begin{equation} a^{*}=\frac{a_{2}}{\bar{a}}, \quad \lambda<x / L<1 \tag{4b} \end{equation}
$$
$\bar{a}$ はパターン率の平均値、式(5)で示されている。
$$
\begin{equation} \bar{a}=\lambda a_{1}+(1-\lambda) a_{2} \tag{5} \end{equation}
$$
本書では解析モデルおよび、図3 の解析結果を作成する手順を示した。
計算には、$a_{1}=0.1、a_{2}=0.9、\lambda=0.5、\mathrm{~L}=1 \mathrm{~mm}$ とする。電解質を、導電率 $10 \mathrm{~S} / \mathrm{m}$ の硫酸銅水溶液であると想定する。式(3)によって、 $W a_{\mathrm{T}}$ 数を 0.1 と 1 に対する総電流をアノード表面に印加し、2次電流分布を計算する。
図3 に電解質電位、電解質電流およびカソード表面の電流分布を示している。パターン率が低い側(この例では左側)でカソード電流密度が高いことという一般的な結果はここに再現された。
これによって、シード層の大部分がフォトレジストによって隠されている領域に、より厚いめっき物が予想できる。ただし、$W a_{\mathrm{T}}$数が高くなると、カソード電流密度のプロファイルが均一になり、大きい$W a_{\mathrm{T}}$数があったカソード表面の電流分布は均一性が良くなる傾向が検証された。
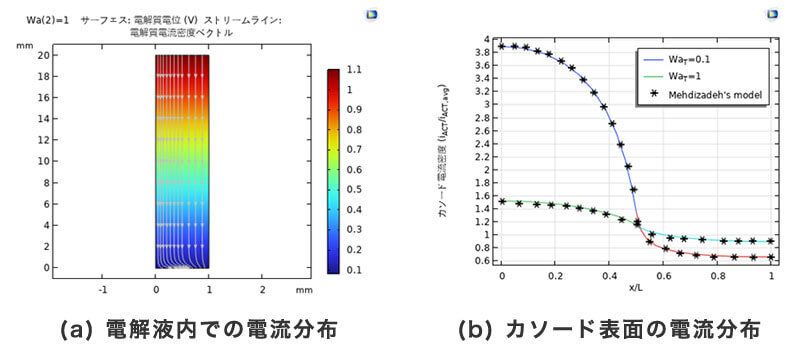
図 3. パターンめっきにおける電流分布の計算結果.
参考文献
- S. Mehdizadeh, J. O. Dukovic, P. C. Andricacos, L. T. Romankiw and H. Y. Cheh: The Influence of Lithographic Patterning on Current Distribution: A Model for Microfabrication by Electrodeposition, J. Electrochem. Soc. 139 78 (1992).
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりダウンロードいただけます。