ヘリウムガスを用いたプラズマ弾丸伝播型の大気圧プラズマジェットを誘電体プレートに照射すると,プレートをトンネルして伝播するかように,プレートの裏面側にプラズマジェットが現れることがある.このプラズマジェットのトンネル現象は,通常の物質輸送型のジェットではあり得ない現象であり,学術的に極めて興味深い現象である1).
プラズマ弾丸が誘電体をトンネリングするという現象は,弾丸着弾時の蓄積電荷由来の局所電場によって裏面側に新たなプラズマ弾丸を生成するというメカニズムで説明される.そのため,誘電体板の片面に高電圧パルスを印加すると,誘電体板の反対側の面に接する空間がヘリウムで満たされている場合には,表面発射型プラズマ弾丸と呼ばれる局所的放電の伝播が生じる.本モデルは,その現象をCOMSOL Multiphysicsâに備わっているアダプティブメッシュを利用して再現するモデルである.
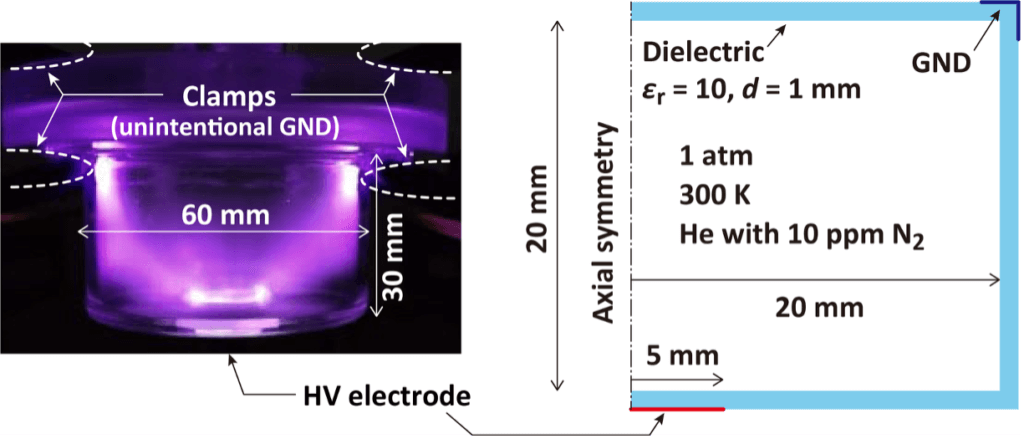
計算用のジオメトリは図1に示した2D軸対称モデルとし,実験系におおよそ一致するようにした.ガスはヘリウムと微量窒素(10 ppm),温度は300 K, 圧力は1 atmである.カソードは接地し,アノードは電圧が7 kVで印加される.
本書ではモデルおよび,図4の解析結果を作成する手順を示す.計算モデルは,電子,イオンと中性粒子の輸送,空間電荷場の計算方程式を連立して計算を行うが,紙数の都合でここではこれらの方程式の説明2)を省略する.
プラズマ弾丸の伝播という放電現象を記述できる最低限の反応として,以下の反応を考慮した.
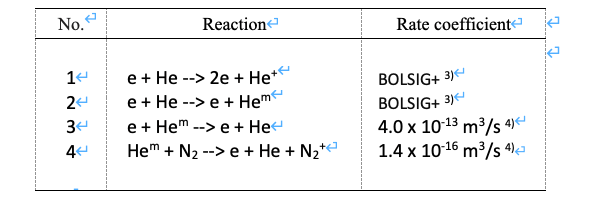
式(1)と(2)の電子衝突反応レート係数は,ボルツマン解析ソフトBOLSIG+ 3)で求められ, 計算結果を図2に示している.Hemはヘリウム原子の準安定励起状態である.実際には,2つの準安定励起状態が存在するが,本モデルでは,簡単化のためにそれらを区別しないこととした.つまり,それぞれに励起される電子衝突断面積は異なるが,本モデルではそれらの和を使用した.なお,光イオン化も種電子の供給源として重要視されているが,本モデルでは,比較的大きい初期電子密度を仮定しているので,光イオン化は考慮していない.プラズマ弾丸の伝播では,プラズマ弾丸の伝播では,微量の窒素がヘリウムの準安定励起原子によってイオン化されることも,重要視されているので,He 100%のモデルではなく,N2が存在する放電反応系の最も簡単化したものとした.
プラズマ弾丸モデルの作成において,計算領域のメッシング生成は重要な要素の1つである.プラズマ弾丸の伝搬に応じて,アダプティブメッシュ細分化(Adaptive Mesh Refinement,AMR)法が有効になっている.図3にCOMSOLのアダプティブメッシュ細分化の設定画面を示す.アダプティブメッシュ細分化では,放電における急峻な変化をする部分で細かいメッシュにすることができる.
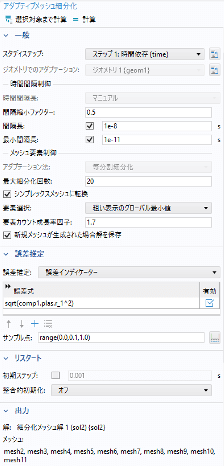
その際の指標となる量を誤差インディケーターに入力する.本モデルでは,イオン化レートが急峻に変化する部分を細かいメッシュにするために,sqrt(comp1.plas.r_1^2)とした.plas_r_1はイオン化反応(1)の反応レートである.二乗してルートをとるのは,plas.r_1が負になる可能性を考慮したためである.図3に示す間隔長は,メッシュを再構築する時間間隔である.
したがって,これをあまりにも小さくすると,メッシュ再構築の回数が多くなりすぎるため,計算時間の短縮につながらない可能性があるので,注意を要する.本モデルは,間隔長を10 nsにすると,計算が3分15秒になるのに対し,1 nsにすると22分52秒(通常のメッシュで「極めて細かい」を選択した場合と同等)となる.計算用のパソコンスペックは以下の通りである.
- OS: WINDOWS 11
- CPU: Intel(R) Xeon(R) Gold 6334 CPU @ 3.60GHz (3.70 GHz)
- メモリ(RAM):128 GB
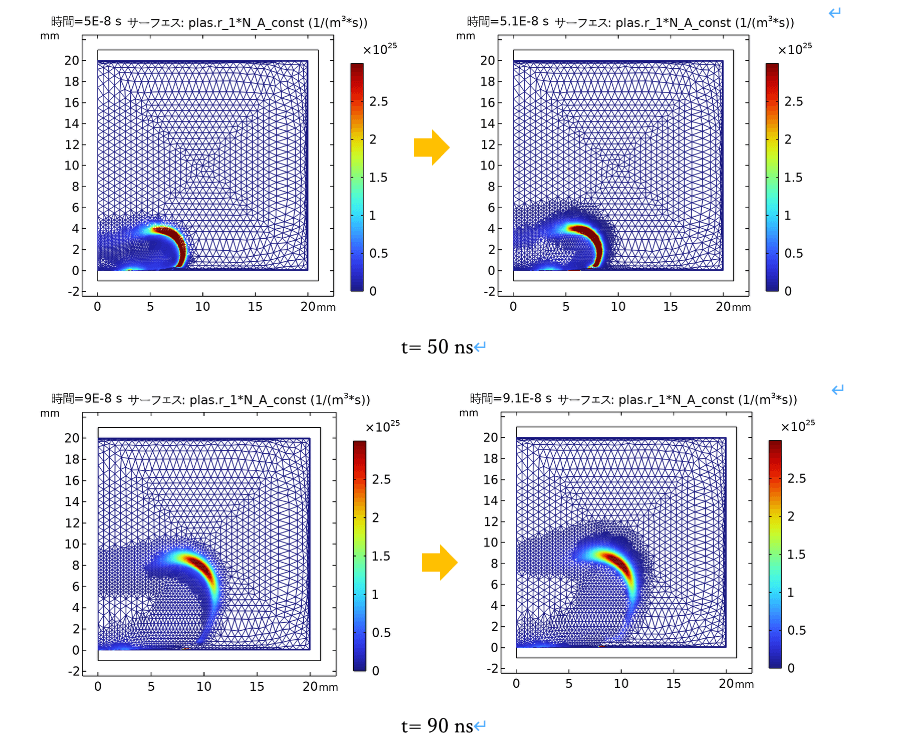
計算には電子エネルギー分布関数をマックスウェル,誘電体表面にイオン衝突による二次電子放出係数を0.01,二次電子平均エネルギーを4とする.また,誘電体表面にイオンと励起種の付着係数は1である.100 nsまで計算を行った.図4は間隔長を10 nsにした場合の計算結果,ワイヤーフレームで表したイオン化レート(プラズマ弾丸に相当)である.50 nsと90 nsの時にメッシュを更新する様子を示すように,イオン化レートの高いところ(プラズマ弾丸の場所)において,メッシュが細かくなっていることが再現され,アダプティブメッシュが機能していることを検証した.
参考文献
- 白藤 立,プラズマ弾丸「トンネリング」現象とその応用展望,応用物理,95(1),2026.
- 放電・プラズマ気相シミュレーション技法調査専門委員会編,「放電・プラズマ気相シミュレーション技法:佟立柱,竹内希,3.3 COMSOL Multiphysicsを用いた非熱プラズマと熱プラズマの計算」,電気学会技術報告第1488号,pp. 70-74 (2020).
- G. J. M. Hagelaar and L. C. Pitchford, Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models, Plasma Sources Sci. Technol., 14 (2005) 722-733.
- H. Halfmann, Characterization of low pressure double inductively coupled plasmas, determination of fundamental sterilization mechanisms and surface modifications of medical materials, Ph.D Thesis, Ruhr-University, Bochum, 2008, p. 42.
*該当のCOMSOLモデルファイルをご要望のお客様は以下よりご請求ください。