確率変数\(\ X\ \)が取り得る離散値を\(\ (x_1,\cdots,x_m) \ \)とし、離散値それぞれに対応する確率\(\ (p_1,\cdots,p_m) \ \)が存在するとき、確率変数\(\ X\ \)を離散型確率変数という。離散型確率変数\(\ X\ \)が任意の離散値\(\ x\ \)をとる関数を\(\ f(x)\ \)としたとき、\(\ f(x)\ \)を確率質量関数と呼ぶ。 \[f(x_i)=P\,(X=x_i) \tag{1.1}\] \[P\,(X=x_i)=P_X(x_i)=p_i \tag{1.2}\] 確率質量関数\(\ P_X(x_i)\ \)については、以下の条件を満足する必要がある。 \[0\le P_X(x_i)\le 1 \tag{1.3}\] \[ \sum_{i=1}^m P_X(x_i)=1 \tag{1.4}\] 一方、確率変数\(\ X\ \)が連続値の場合には、式 (1.2) による確率\(\ P_X(x)\ \)は常に\(\ 0\ \)となる。そこで、次式で確率変数\(\ \ X\ \)が\(\ a\le X \le b\ \)となる確率を表す。このとき、\(\ f(x)\ \)を確率密度関数と呼ぶ。 \[\int_a^bf(x)dx=P\,(a\le X\le b) \tag{1.5}\] \[p\,(X=x)=p_X(x) \tag{1.6}\] 確率密度関数\(\ p_X\,(x)\ \)については、以下の関係が成立する。 \[p_X(x)\ge0 \tag{1.7}\] \[\int_{-\infty}^{\infty} p_X\, (x)dx=1 \tag{1.8}\] 文脈により確率変数を明示する必要がないときには、確率質量あるいは単に確率(確率質量関数)を\(\ P\,(x)\ \)、確率密度(確率密度関数)を\(\ p\,(x) \ \)と表す。
2つの離散型確率変数確率変数\(\ X\ \)と\(\ Y\ \)の確率質量関数を考える。 \[P_X(X=x_i)=P_X(x_i)\ ,\quad i=1,\cdots,m \tag{2.1}\] \[P_Y(Y=y_j)=P_Y(y_j)\ ,\quad j=1,\cdots,n \tag{2.2}\]
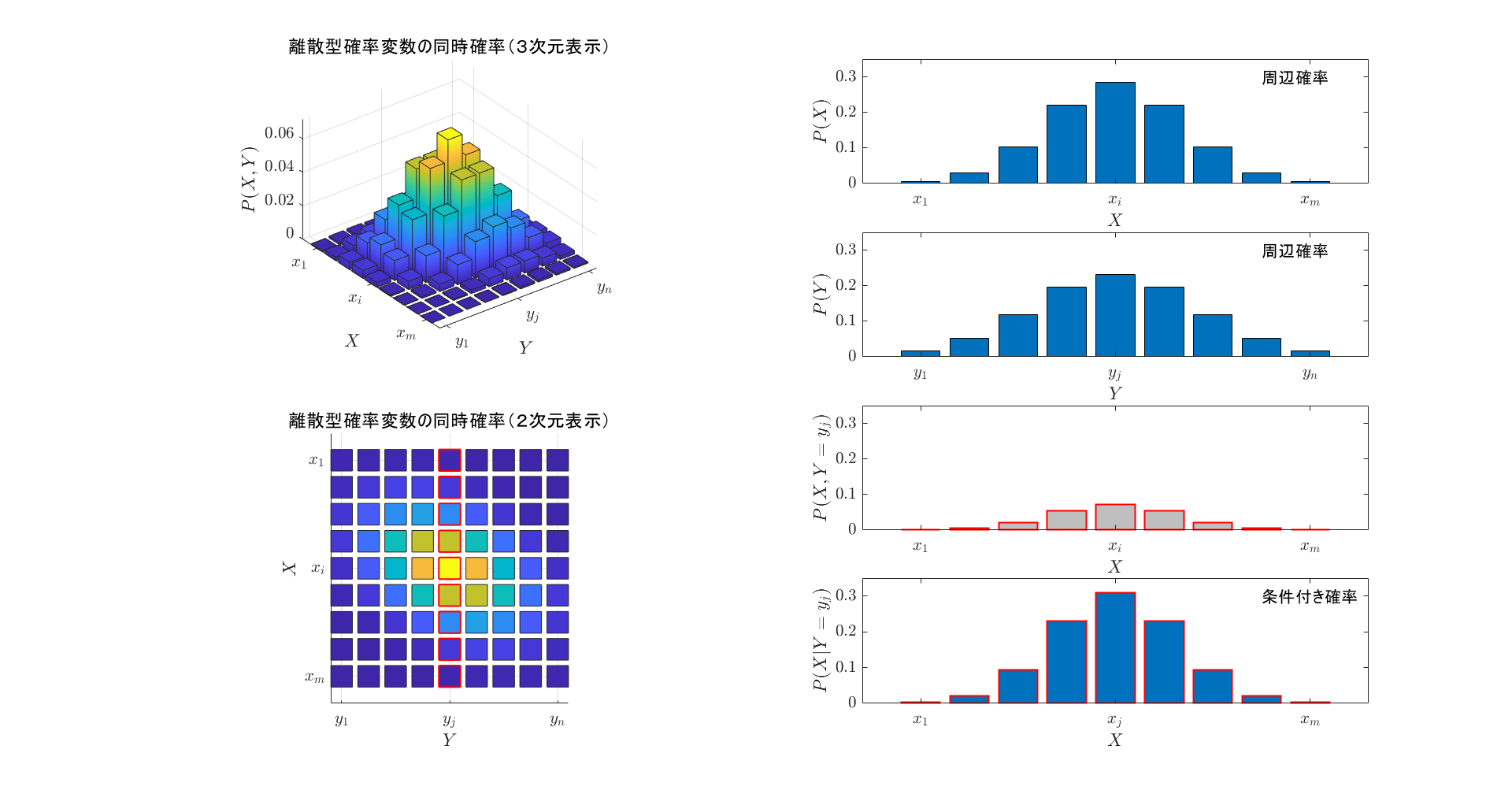
2つの離散型確率変数が\(\ X=x_i\ \)かつ\(\ Y=y_j\ \)となる同時確率を次式で定義する。 \[P_{X\cap Y}(X=x_i \cap Y=y_j)=P\,(X=x_i \cap Y=y_j) \tag{2.3}\] 以下、確率変数を明示せず同時確率を\(\ P\,(x_i,y_j)\ \)と表すこととすると、以下の関係が成立する。 \[P\,(x_i,y_j)\ge0 \tag{2.4}\] \[ \sum_{i=1}^m \sum_{j=1}^n P\,(x_i,y_j)=1 \tag{2.5}\] 図 1 の左上に同時確率の例を示す。
同時確率分布\(\ P\,(X,Y)\ \)の一方の確率分布に着目し、その総和によって定義される確率分布を周辺確率という。 \[\sum_{j=1}^n P\,(x_i,y_j) = P\,(X=x_i) \ ,\quad i=1,\cdots.m \tag{2.6}\] \[\sum_{i=1}^m P\,(x_i,y_j) = P\,(Y=y_j) \ ,\quad j=1,\cdots.n \tag{2.7}\] 図 1 の右上に式 (2.6) と (2.7) による周辺確率の例を示す。
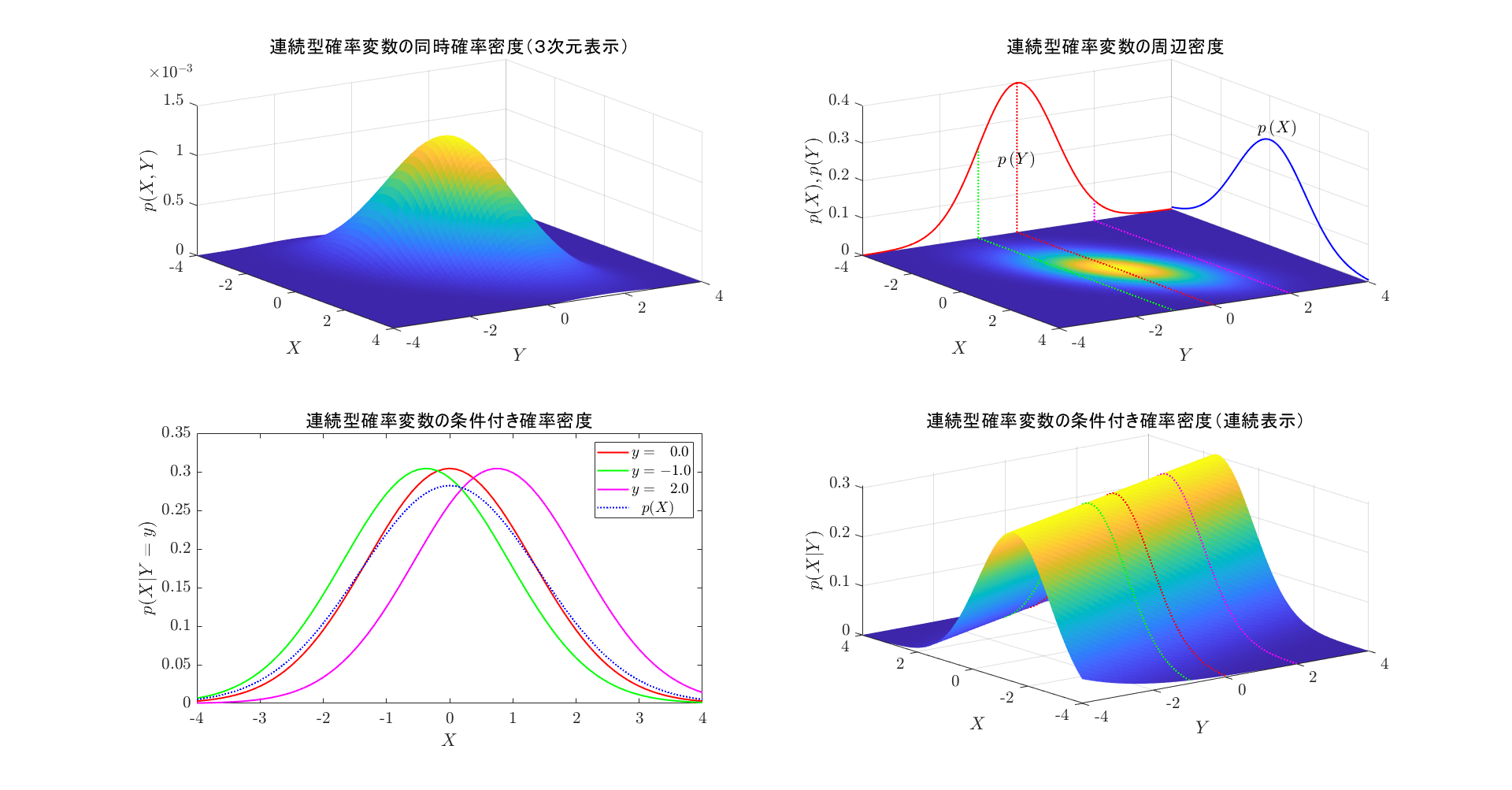
2つの確率変数が\(\ X=x\ \)かつ\(\ Y=y\ \)となる確率密度を同時確率密度という(図 2 左上)。式 (2.4) (2.5) に対応する関係が成立する。 \[p\,(x,y)=p\,(X=x \cap Y=y) \tag{3.1}\] \[p\,(x,y)\ge0 \tag{3.2}\] \[\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p\,(x,y)\,dxdy=1 \tag{3.3}\]
同時確率密度分布\(\ p\,(X,Y)\ \)から以下に定義する周辺確率密度分布が定義される(図 2 右上)。 \[\int_{-\infty}^{\infty} p\,(X,Y)\,dY=p\,(X) \tag{3.4}\] \[\int_{-\infty}^{\infty} p\,(X,Y)\,dX=p\,(Y) \tag{3.5}\]
同時確率密度分布\(\ p\,(X,Y)\ \)から以下に定義する条件付き確率密度分布が定義される。
\[p\,(X\,|\,Y=y)=\frac{p\,(X,Y=y)}{p\,(Y=y)} \tag{3.6}\]
\[p\,(Y\,|\,X=x)=\frac{p\,(Y,X=x)}{p\,(X=x)} \tag{3.7}\]
図 2 右上の3本の点線で示される\(\ Y=y\ \)の平面で切り出した同時確率密度分布と周辺確率密度から求めた条件付き確率密度を図 2 左下に示す。\(¥X\ \)の周辺確率密度分布も点線で重ねて表示している。
この例では、条件付き確率密度は1次元の分布であるが、全体の振舞いを理解するために、確率密度を連続的に配置した2次元空間での分布を図 2 右下に示す(左上の同時確率密度とは異なることに注意が必要である)。
式 (2.3) による定義
\(\ P_{X\cap Y}(X=x_i \cap Y=y_j)=P\,(X=x_i \cap Y=y_j) \ \)を
\[P_{X\cap Y}(X=x_i \cap Y=y_j)=P\,(X=x_i)\cdot P\,(Y=y_j) \ \tag{4.1}\]
と勘違いしてはいけない。式 (4.1) は常に成立することはなく、成立する場合2つの確率変数は独立であるという。
2つの確率変数\(\ X\ \)と\(\ Y\ \)が独立であるとき、以下の関係が成り立つ。この関係は確率についても成立する。条件付き分布がもう一方の確率変数に関わらず周辺分布と一致することを表していて、図 2 の左下で考えると、3本の条件付き密度が点線の周辺分布に一致することになる。
\[p\,(X\,|\,Y)=p\,(X) \tag{4.2}\]
\[p\,(Y\,|\,X)=p\,(Y) \tag{4.3}\]
式 (3.6) と (3.7) を確率密度で表すと、 \[p\,(x\,|\,y)=\frac{p\,(x,y)}{p\,(y)} \tag{5.1}\] \[p\,(y\,|\,x)=\frac{p\,(y,x)}{p\,(x)} \tag{5.2}\] となる。\(\ p\,(x,y)=p\,(y,x)\ \)であるので、式 (5.1) を変形して得られる\(\ p\,(x,y)\ \)を式 (5.2) に代入すると \[p\,(y\,|\,x)=\frac{p\,(x\,|\,y)\,p\,(y)}{p\,(x)} =\frac{p\,(x\,|\,y)\,p\,(y)}{\int p\,(x\, |\,y)\,p\,(y)\,dy}\ \tag{5.3}\] となる。この関係をベイズの定理と呼ぶ。
確率変数\(\ X\ \)がパラメータ\(\ \theta\ \)に支配されていると仮定し、条件付き確率密度\(\ p\,(\theta \,|\,x)\ \)を考える。パラメータがある確率密度\(\ p\,(\theta )\ \)であるとき、新しいデータ\(\ x\ \)があたえられたときの新たなパラメータの確率密度が\(\ p\,(\theta \,|\,x)\ \)になるということを表している。式 (5.3) を書き直すと
\[p\,(\theta \,|\,x)=\frac{p\,(x\,|\,\theta )\,p\,(\theta )}{p\,(x)} =\frac{p\,(x\,|\,\theta )\,p\,(\theta )}{\int p\,(x\,|\,\theta )\,p\,(\theta ) \,d\theta}\ \tag{5.4}\]
が得られる。この式に現れる\(\ p\,(x\,|\,\theta )\ \)は、見かけでは条件付き確率密度の形式となっているが、新たなパラメータの確率密度から原因となったデータを推測する尤もらしさを表していて、尤度関数(単に尤度)と呼ぶ。尤度関数を\(\ f\,(x\,|\, \theta )\ \)と改めて書くと、ベイズの定理は
\[p\,(\theta \,|\,x)=\frac{f\,(x\,|\,\theta )\,p\,(\theta )}{p\,(x)} =\frac{f\,(x\,|\,\theta )\,p\,(\theta )}{\int f\,(x\,|\,\theta )\,p\,(\theta ) \,d\theta}\ \tag{5.5}\]
と表すことができる
この式に現れるそれぞれの項によって以下の関係が示される。分母は尤度関数を\(\ \theta \ \)で積分する周辺化を表すことから周辺尤度と呼ぶ。
\[\text{事後確率密度}=\frac{\text{尤度}\times \text{事前確率密度}}{\text{周辺尤度}}\]
周辺尤度は\(\ \theta \ \)の関数ではないため正規化定数と考えて
\[\text{事後確率密度}\propto \text{尤度}\times \text{事前確率密度}\]
と表すこともある。