前回の強形式編の記事で紹介したように、なるべく構成関係を線形に仮定した幾何形状の変化を考慮した支配方程式は次のようになります。

$$
\begin{aligned}
\boldsymbol{\nabla}_{\boldsymbol{x}} \cdot \boldsymbol{\sigma}+\mathbf{f}_{\boldsymbol{v}}=\mathbf{0} & \quad \text { in } \Omega_{\mathrm{t}} \\
\boldsymbol{\sigma}=\boldsymbol{J}^{-1} \mathbb{C}: \boldsymbol{\varepsilon} & \quad \text { in } \Omega_{\mathrm{t}} \\
\boldsymbol{\varepsilon}=\ln \boldsymbol{V} & \quad \text { in } \Omega_{\mathrm{t}} \\
\boldsymbol{\sigma} \cdot \boldsymbol{n}=\mathbf{f}_{\boldsymbol{a}} & \quad \text { on } \partial \Omega_{\mathrm{a}}^{\mathrm{t}} \\
\boldsymbol{u}=\overline{\boldsymbol{u}} & \quad \text { on } \partial \Omega_{\mathrm{u}}^{\mathrm{t}}
\end{aligned}
$$

有限要素解析は弱形式に基づいているため、これからまずこの境界値問題を弱形式に書き換えます。こ こで、未知関数 $\boldsymbol{u}$ と試験関数 $\boldsymbol{\eta}$ を次の 2 つの関数空間に限定します。
$$
\begin{gathered}
\boldsymbol{u} \in \mathcal{V}, \quad \mathcal{V}=\left\{\boldsymbol{u} \mid \boldsymbol{u} \in H^{1}\left(\Omega_{\mathrm{t}}\right), \boldsymbol{\nabla} \boldsymbol{u} \in L^{\infty}\left(\Omega_{\mathrm{t}}\right), \boldsymbol{u}(\boldsymbol{x}, t)=\overline{\boldsymbol{u}}(\boldsymbol{x}, t) \text { for } t \in\left[t_{0}, t_{1}\right], \boldsymbol{x} \in \partial \Omega_{\mathbf{u}}^{\mathrm{t}}\right\} \\
\boldsymbol{\eta} \in \mathcal{W}, \quad \mathcal{W}=\left\{\boldsymbol{\eta} \mid \boldsymbol{\eta} \in H^{1}\left(\Omega_{\mathrm{t}}\right), \boldsymbol{\eta}(\boldsymbol{x})=\mathbf{0} \text { for } \boldsymbol{x} \in \partial \Omega_{\mathbf{u}}^{\mathrm{t}}\right\}
\end{gathered}
$$

つぎに、平衡方程
$$
\boldsymbol{\nabla}_{\boldsymbol{x}} \cdot \boldsymbol{\sigma}+\mathbf{f}_{\boldsymbol{v}}=\mathbf{0} \quad \text { in } \Omega_{\mathrm{t}}
$$

の両辺に任意の $\boldsymbol{\eta} \in \mathcal{W}$ を作用させると、次式を得ます。
$$
\begin{aligned}
0 & =\int_{\Omega_{\mathrm{t}}}\left(\boldsymbol{\nabla}_{\boldsymbol{x}} \cdot \boldsymbol{\sigma}+\mathbf{f}_{v}\right) \cdot \boldsymbol{\eta} d v \\
& =\int_{\Omega_{\mathrm{t}}}\left(\boldsymbol{\nabla}_{\boldsymbol{x}} \cdot \boldsymbol{\sigma}\right) \cdot \boldsymbol{\eta} d v+\int_{\Omega_{\mathrm{t}}} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d v \\ & =\int_{\Omega_{\mathrm{t}}}\left(\sigma_{i j, i} \eta_{j}\right) d v+\int_{\Omega_{\mathrm{t}}} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d v \\ & =\int_{\Omega_{t}}\left(\sigma_{i j} \eta_{j}\right){, i} d v-\int_{\Omega_{t}} \sigma_{i j} \eta_{j, i} d v+\int_{\Omega_{t}} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d v \\ & =\int_{\Omega_{\mathrm{t}}} \boldsymbol{\nabla}_{\boldsymbol{x}} \cdot(\boldsymbol{\sigma} \cdot \boldsymbol{\eta}) d v-\int_{\Omega_{\mathrm{t}}} \boldsymbol{\sigma}: \boldsymbol{\nabla}_{\boldsymbol{x}} \boldsymbol{\eta} d v+\int_{\Omega_{\mathrm{t}}} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d v
\end{aligned}
$$

ここでは便宜上、総和規約を使用しました。例えば、 $\left(\sigma_{i j} \eta_{j}\right)_{, i}$ はと次のようになります。
$$
\begin{aligned} \left(\sigma{i j} \eta_{j}\right){, i}= & \sum_{i=1}^{3} \sum_{j=1}^{3} \frac{\partial \sigma_{i j} \eta_{j}}{\partial x^{i}} \\
= & \frac{\partial \sigma_{11} \eta_{1}}{\partial x^{1}}+\frac{\partial \sigma_{12} \eta_{2}}{\partial x^{1}}+\frac{\partial \sigma_{13} \eta_{3}}{\partial x^{1}} \\
& +\frac{\partial \sigma_{21} \eta_{1}}{\partial x^{2}}+\frac{\partial \sigma_{22} \eta_{2}}{\partial x^{2}}+\frac{\partial \sigma_{23} \eta_{3}}{\partial x^{2}} \\
& +\frac{\partial \sigma_{31} \eta_{1}}{\partial x^{3}}+\frac{\partial \sigma_{32} \eta_{2}}{\partial x^{3}}+\frac{\partial \sigma_{33} \eta_{3}}{\partial x^{3}}
\end{aligned}
$$

ガウスの発散定理を用いると、
$$
0=\int_{\partial \Omega_{\mathrm{a}}^{\mathrm{t}}} \boldsymbol{n} \cdot \boldsymbol{\sigma} \cdot \boldsymbol{\eta} d s-\int_{\Omega_{\mathrm{t}}} \boldsymbol{\sigma}: \boldsymbol{\nabla}_{x} \boldsymbol{\eta} d v+\int_{\Omega_{\mathrm{t}}} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d v $$ $\sigma$ の対称性を用いて $\nabla_{x} \eta$ の反対称成分を除けば $\sigma: \nabla_{x} \eta=\sigma: \nabla_{x}^{s} \eta$ となるため、
$$
=\int_{\partial \Omega_{\mathrm{a}}^{\mathrm{t}}} \boldsymbol{n} \cdot \boldsymbol{\sigma} \cdot \boldsymbol{\eta} d s-\int_{\Omega_{\mathrm{t}}} \boldsymbol{\sigma}: \boldsymbol{\nabla}_{\boldsymbol{x}}^{s} \boldsymbol{\eta} d v+\int_{\Omega_{\mathrm{t}}} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d v
$$

境界条件 $\boldsymbol{\sigma} \cdot \boldsymbol{n}=\mathbf{f}_{\boldsymbol{a}} \quad$ on $\partial \Omega_{\mathrm{a}}^{\mathrm{t}}$ を考慮すると、
$$
0=\int_{\Omega_{\mathrm{t}}} \boldsymbol{\sigma}: \boldsymbol{\nabla}_{\boldsymbol{x}}^{s} \boldsymbol{\eta} d v-\int_{\partial \Omega_{\mathrm{a}}^{\mathrm{t}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d s-\int_{\Omega_{\mathrm{t}}} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d v
$$

になり、最終的に弱形式は
$$
\begin{aligned}
& \text { Find } \boldsymbol{u} \in \mathcal{V}, \quad \mathcal{V}=\left\{\boldsymbol{u} \mid \boldsymbol{u} \in H^{1}\left(\Omega_{\mathrm{t}}\right), \boldsymbol{\nabla} \boldsymbol{u} \in L^{\infty}\left(\Omega_{\mathrm{t}}\right), \boldsymbol{u}(\boldsymbol{x}, t)=\overline{\boldsymbol{u}}(\boldsymbol{x}, t) \text { for } t \in\left[t_{0}, t_{1}\right], \boldsymbol{x} \in \partial \Omega_{\mathrm{u}}^{\mathrm{t}}\right\} \\
& \quad 0=\int_{\Omega_{\mathrm{t}}} \boldsymbol{\sigma}: \boldsymbol{\nabla}_{\boldsymbol{x}}^{s} \boldsymbol{\eta} d v-\int_{\partial \Omega_{\mathrm{a}}^{\mathrm{t}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d s-\int_{\Omega_{\mathrm{t}}} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d v \quad(\forall \boldsymbol{\eta} \in \mathcal{W}) \\ & \boldsymbol{\eta} \in \mathcal{W}, \quad \mathcal{W}=\left\{\boldsymbol{\eta} \mid \boldsymbol{\eta} \in H^{1}\left(\Omega_{\mathrm{t}}\right), \boldsymbol{\eta}(\boldsymbol{x})=\mathbf{0} \text { for } \boldsymbol{x} \in \partial \Omega_{\mathrm{u}}^{\mathrm{t}}\right\}
\end{aligned}
$$

になります。一方、微小変形の弱形式については、配置を区別しないように（ $\Omega_{\mathrm{t}} \rightarrow \Omega \Rightarrow \boldsymbol{\nabla}_{\boldsymbol{x}}^{s} \rightarrow \boldsymbol{\nabla}^{s}$ ）

に変更すれば、以下のように書き換えられます。
$$
\begin{aligned}
& \text { Find } \boldsymbol{u} \in \mathcal{V}, \quad \mathcal{V}=\left\{\boldsymbol{u} \mid \boldsymbol{u} \in H^{1}(\Omega), \boldsymbol{u}(\boldsymbol{x}, t)=\overline{\boldsymbol{u}}(\boldsymbol{x}, t) \text { for } t \in\left[t_{0}, t_{1}\right], \boldsymbol{x} \in \partial \Omega_{\mathbf{u}}\right\} \\
& \qquad \begin{array}{c}
0=\int_{\Omega} \boldsymbol{\sigma}: \boldsymbol{\nabla}^{s} \boldsymbol{\eta} d V-\int_{\partial \Omega_{\mathrm{a}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d S-\int_{\Omega} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d V \quad(\forall \boldsymbol{\eta} \in \mathcal{W}) \\ \mathcal{W}=\left\{\boldsymbol{\eta} \mid \boldsymbol{\eta} \in H^{1}(\Omega), \boldsymbol{\eta}(\boldsymbol{x})=\mathbf{0} \text { for } \boldsymbol{x} \in \partial \Omega_{\mathbf{u}}\right\}
\end{array}
\end{aligned}
$$

　幾何学的非線形を扱う有限要素固体解析には、一般的に 2 種類の定式化方法があります。 1 つは Updated Lagrange（更新ラグランジュ）法で、計算途中の配置を積分領域として逐次更新しなが ら解きます。もう 1 つは Total Lagrange（トータルラグランジュ）法で、初期配置を積分領域として用 います。両者は等価的に同じ連続体問題を記述できます。図 1 に示すように、COMSOL Multiphysics ${ }^{\text {® }}$ では「トータルラグランジュ」、「幾何学的線形」といった選択肢が現れます。「トータルラグ ランジュ」は Total Lagrange 法を用いた幾何学的非線形解析となります。一方、「幾何学的線形」は幾何学的非線形を考慮しない微小変形解析を意味します。

「トータルラグランジュ」法を選ぶと、先ほどの弱形式は初期配置へ引き戻されます。まず表面力項は、
$$
\begin{aligned}
& \int_{\partial \Omega_{\mathrm{a}}^{\mathrm{t}}} \mathbf{f}_{a} \cdot \boldsymbol{\eta} d s \\ & =\int_{\partial \Omega_{\mathrm{a}}^{\mathrm{t}}} \boldsymbol{\eta} \cdot(\boldsymbol{\sigma} \cdot \boldsymbol{n}) d s \\
& =\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0}(\boldsymbol{X}) \cdot \boldsymbol{\sigma} \cdot\left(J \boldsymbol{F}^{-T} \cdot \boldsymbol{N}\right) d S \\
& =\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \boldsymbol{F} \boldsymbol{F}^{-1} \boldsymbol{\sigma} J \boldsymbol{F}^{-T} \cdot \boldsymbol{N} d S \\
& =\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \boldsymbol{F} \boldsymbol{S} \cdot \boldsymbol{N} d S \\
& =\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \mathbf{f}_{A}^{0} d S
\end{aligned}
$$

ここでは Nanson の公式を用いて面積ベクトルを変換しました。同様に体積力項については、
$$
\int_{\Omega_{\mathrm{t}}} \mathbf{f}_{v} \cdot \boldsymbol{\eta} d v=\int_{\Omega_{0}} J \mathbf{f}_{v} \cdot \boldsymbol{\eta}^{0}(\boldsymbol{X}) d V=\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V
$$

最後に内力項は、以下のように計算できます。
$$
\begin{aligned}
& \int_{\Omega_{\mathrm{t}}} \boldsymbol{\sigma}: \boldsymbol{\nabla}_{\boldsymbol{x}}^{s} \boldsymbol{\eta} d v \\ & =\int_{\Omega_{\mathrm{t}}} \boldsymbol{\sigma}: \boldsymbol{\nabla}_{\boldsymbol{x}} \boldsymbol{\eta} d v \\ & =\int_{\Omega_{\mathrm{t}}} \sigma_{i j}\left(\nabla_{x} \eta\right)_{i j} d v \\ & =\int_{\Omega_{0}} \sigma_{i j}\left(\nabla_{X} \eta^{0}(X)\right)_{i K} F_{K j}^{-1} J d V \\
& =\int_{\Omega_{0}} J \sigma_{i j} F_{K j}^{-1}\left(\nabla_{X} \eta^{0}\right)_{i K} d V \\ & =\int_{\Omega_{0}} F_{i M} F_{M n}^{-1} J \sigma_{n j} F_{j K}^{-T}\left(\nabla_{X} \eta^{0}\right)_{i K} d V \\ & =\int_{\Omega_{0}} F_{i M} S_{M K}\left(\nabla_{X} \eta^{0}\right)_{i K} d V \\ & =\int_{\Omega_{0}} S_{M K} F_{M i}^{T}\left(\nabla_{X} \eta^{0}\right)_{i K} d V \\ & =\int_{\Omega_{0}} \boldsymbol{S}: \boldsymbol{F}^{T} \boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{\eta}^{0} d V \\ & =\int_{\Omega_{0}} \boldsymbol{S}:\left(\operatorname{sym}\left(\boldsymbol{F}^{T} \boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{\eta}^{0}\right)+\mathrm{skw}\left(\boldsymbol{F}^{T} \boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{\eta}^{0}\right)\right) d V \\
& =\int_{\Omega_{0}} \boldsymbol{S}:\left(\operatorname{sym}\left(\boldsymbol{F}^{T} \boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{\eta}^{0}\right)\right) d V \\ & =\int_{\Omega_{0}} \boldsymbol{S}:\left(\operatorname{sym}\left(\boldsymbol{F}^{T} \delta \boldsymbol{F}\right)\right) d V \\
& =\int_{\Omega_{0}} \boldsymbol{S}: \frac{1}{2}\left(\boldsymbol{F}^{T} \delta \boldsymbol{F}+\delta \boldsymbol{F}^{T} \boldsymbol{F}\right) d V \\
& =\int_{\Omega_{0}} \boldsymbol{S}: \delta \boldsymbol{E} d V
\end{aligned}
$$

したがって、初期配置に引き戻した弱形式は次の形になります。ここで、 $\boldsymbol{S}$ が第 2 Piola－Kirchhoff 応 カテンソルと呼ばれています。 $\delta \boldsymbol{E}$ が仮想ひずみテンソルに相当します。
$$
\begin{aligned}
& \text { Find } \boldsymbol{u} \in \mathcal{V}_{0}, \quad \mathcal{V}_{0}=\left\{\boldsymbol{u} \mid \boldsymbol{u} \in H^{1}\left(\Omega_{0}\right), \boldsymbol{\nabla} \boldsymbol{u} \in L^{\infty}\left(\Omega_{0}\right), \boldsymbol{u}(\boldsymbol{X}, t)=\overline{\boldsymbol{u}}(\boldsymbol{X}, t) \text { for } t \in\left[t_{0}, t_{1}\right], \boldsymbol{X} \in \partial \Omega_{\mathbf{u}}^{0}\right\} \\
& 0=\int_{\Omega_{0}} \boldsymbol{S}: \delta \boldsymbol{E} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \mathbf{f}_{\boldsymbol{A}}^{0} \cdot \boldsymbol{\eta}^{0} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \quad\left(\forall \boldsymbol{\eta}^{0} \in \mathcal{W}_{0}\right) \\
& \mathcal{W}_{0}=\left\{\boldsymbol{\eta}^{0} \mid \boldsymbol{\eta}^{0} \in H^{1}\left(\Omega_{0}\right), \boldsymbol{\eta}^{0}(\boldsymbol{X})=\mathbf{0} \text { for } \boldsymbol{X} \in \partial \Omega_{\mathbf{u}}^{0}\right\}
\end{aligned}
$$

　幾何学的非線形を考慮した有限要素法では、基本的にこの弱形式（積分方程式）を離散化しま す。ここで、 $\mathbf{f}_{A}^{0}$ と $\mathbf{f}_{V}^{0}$ は初期配置上で積分されますが、そのベクトル自体は現在配置に属するものです。 これについて、下図のように COMSOL Multiphysics ${ }^{®}$ の画面上でも現在配置に属する成分（小文字の x，y，z ）を確認できます。

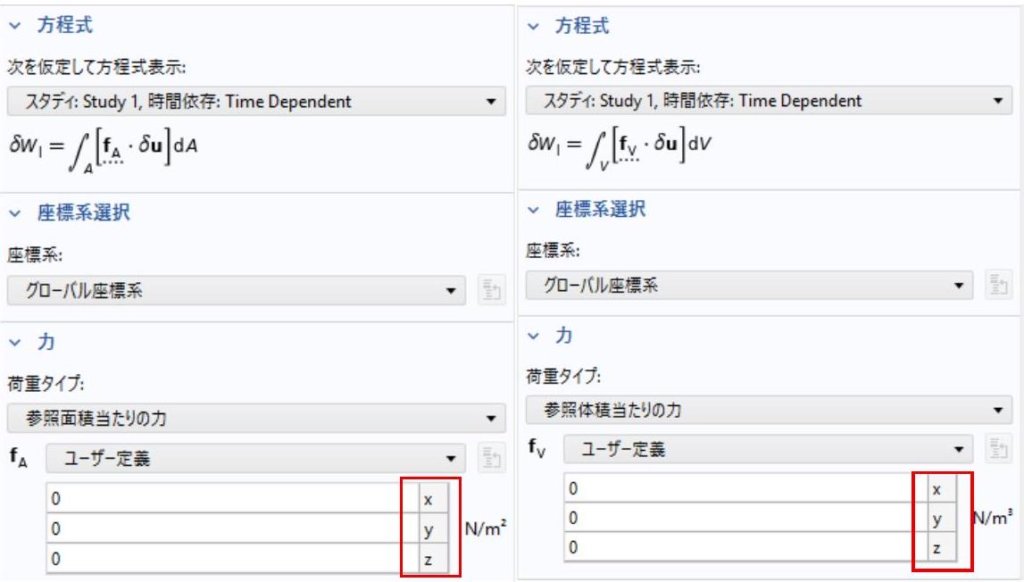
そして、次の操作を行うと、この弱形式と等価な強形式も得られます。
$$
\begin{aligned}
0 & =\int_{\Omega_{0}} \boldsymbol{S}: \delta \boldsymbol{E} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \mathbf{f}_{A}^{0} \cdot \boldsymbol{\eta}^{0} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =\int_{\Omega_{0}} \boldsymbol{S}: \frac{1}{2}\left(\boldsymbol{F}^{T} \delta \boldsymbol{F}+\delta \boldsymbol{F}^{T} \boldsymbol{F}\right) d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \boldsymbol{F} \boldsymbol{S} \cdot \boldsymbol{N} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =\int_{\Omega_{0}} \boldsymbol{S}:\left(\operatorname{sym}\left(\boldsymbol{F}^{T} \delta \boldsymbol{F}\right)\right) d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \boldsymbol{F} \boldsymbol{S} \cdot \boldsymbol{N} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =\int_{\Omega_{0}} \boldsymbol{S}: \boldsymbol{F}^{T} \delta \boldsymbol{F} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \boldsymbol{F} \boldsymbol{S} \cdot \boldsymbol{N} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =\int_{\Omega_{0}} \boldsymbol{S}: \boldsymbol{F}^{T} \boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{\eta}^{0} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \boldsymbol{F} \boldsymbol{S} \cdot \boldsymbol{N} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =\int_{\Omega_{0}} S_{M K} F_{M i}^{T}\left(\nabla_{X} \eta^{0}\right)_{i K} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \boldsymbol{F} \boldsymbol{S} \cdot \boldsymbol{N} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =\int_{\Omega_{0}} S_{M K} F_{M i}^{T} \eta_{i, K}^{0} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \boldsymbol{F} \boldsymbol{S} \cdot \boldsymbol{N} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =\int_{\Omega_{0}}\left(S_{K M} F_{M i}^{T} \eta_{i}^{0}\right)_{, K} d V-\int_{\Omega_{0}}\left(S_{K M} F_{M i}^{T}\right){, K} \eta{i}^{0} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{\eta}^{0} \cdot \boldsymbol{F} \boldsymbol{S} \cdot \boldsymbol{N} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =\int_{\Omega_{0}} \boldsymbol{\nabla}_{\boldsymbol{X}} \cdot\left(\boldsymbol{S} \boldsymbol{F}^{T} \cdot \boldsymbol{\eta}^{0}\right) d V-\int_{\Omega_{0}} \boldsymbol{\nabla}_{\boldsymbol{X}} \cdot\left(\boldsymbol{S} \boldsymbol{F}^{T}\right) \cdot \boldsymbol{\eta}^{0} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{N} \cdot \boldsymbol{S} \boldsymbol{F}^{T} \cdot \boldsymbol{\eta}^{0} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =\int_{\partial \Omega_{0}} \boldsymbol{N} \cdot\left(\boldsymbol{S} \boldsymbol{F}^{T} \cdot \boldsymbol{\eta}^{0}\right) d S-\int_{\Omega_{0}} \boldsymbol{\nabla}_{\boldsymbol{X}} \cdot\left(\boldsymbol{S} \boldsymbol{F}^{T}\right) \cdot \boldsymbol{\eta}^{0} d V-\int_{\partial \Omega_{\mathrm{A}}^{0}} \boldsymbol{N} \cdot \boldsymbol{S} \boldsymbol{F}^{T} \cdot \boldsymbol{\eta}^{0} d S-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =-\int_{\Omega_{0}} \boldsymbol{\nabla}_{\boldsymbol{X}} \cdot\left(\boldsymbol{S} \boldsymbol{F}^{T}\right) \cdot \boldsymbol{\eta}^{0} d V-\int_{\Omega_{0}} \mathbf{f}_{V}^{0} \cdot \boldsymbol{\eta}^{0} d V \\ & =-\int_{\Omega_{0}}\left\{\boldsymbol{\nabla}_{\boldsymbol{X}} \cdot\left(\boldsymbol{S} \boldsymbol{F}^{T}\right)+\mathbf{f}_{V}^{0}\right\} \cdot \boldsymbol{\eta}^{0} d V \\
& =\int_{\Omega_{0}}\left\{\boldsymbol{\nabla}_{\boldsymbol{X}} \cdot(\boldsymbol{F} \boldsymbol{S})^{T}+\mathbf{f}_{V}^{0}\right\} \cdot \boldsymbol{\eta}^{0} d V
\end{aligned}
$$

上式は任意の $\boldsymbol{\eta}^{0} \in \mathcal{W}_{0}$ に対して成立しなければならないため、 $$ \begin{gathered} \boldsymbol{\nabla}_{\boldsymbol{X}} \cdot(\boldsymbol{F} \boldsymbol{S})^{T}+\mathbf{f}_{V}^{0}=\mathbf{0} \quad \text { in } \Omega_{0} \\
\boldsymbol{\nabla}_{\boldsymbol{X}} \cdot\left(\left(\boldsymbol{I}+\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right) \boldsymbol{S}\right)^{T}+\mathbf{f}_{V}^{0}=\mathbf{0} \quad \text { in } \Omega_{0}
\end{gathered}
$$

が得られます（ $\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u} \equiv \boldsymbol{u} \otimes \boldsymbol{\nabla}_{\boldsymbol{X}}$ ）。「トータルラグランジュ」を選択すると、以下の図に示すように、 COMSOL Multiphysics ${ }^{®}$ の画面上の方程式も幾何学的非線形を考慮した方程式に変わります。

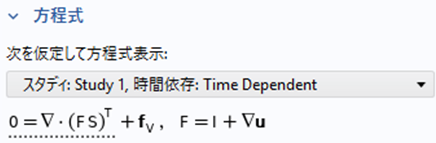
このとき材料を線形（Saint－Venant－Kirchhoff モデル）と仮定すれば、応力とひずみは
$$
\boldsymbol{S}=\mathbb{C}: \boldsymbol{E}
$$
の線形関係になります。ここで、 $\boldsymbol{E}$ が Green－Lagrange ひずみテンソルと呼ばれています。
$$
\begin{aligned}
\boldsymbol{E} & =\frac{1}{2}\left(\boldsymbol{F}^{T} \boldsymbol{F}-\boldsymbol{I}\right) \\
& =\frac{1}{2}\left[\left(\boldsymbol{I}+\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right)^{T}\left(\boldsymbol{I}+\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right)-\boldsymbol{I}\right] \\
& =\frac{1}{2}\left[\left(\boldsymbol{I}+\left(\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right)^{T}\right)\left(\boldsymbol{I}+\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right)-\boldsymbol{I}\right] \\
& =\frac{1}{2}\left[\left(\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right)^{T}+\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}+\left(\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right)^{T} \boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right]
\end{aligned}
$$
$\boldsymbol{F}$ が変位 $\boldsymbol{u}$ の関数であるため、 $\boldsymbol{E}$ が変位 $\boldsymbol{u}$ の非線形関数になります。つまり、現在配置における強形式
$$
\begin{aligned}
\boldsymbol{\nabla}_{\boldsymbol{x}} \cdot \boldsymbol{\sigma}+\mathbf{f}_{\boldsymbol{v}}=\mathbf{0} & \quad \text { in } \Omega_{\mathrm{t}} \\
\boldsymbol{\sigma}=J^{-1} \mathbb{C}: \boldsymbol{\varepsilon} & \quad \text { in } \Omega_{\mathrm{t}} \\
\boldsymbol{\varepsilon}=\ln \boldsymbol{V} & \quad \text { in } \Omega_{\mathrm{t}} \\
\boldsymbol{\sigma} \cdot \boldsymbol{n}=\mathbf{f}_{\boldsymbol{a}} & \quad \text { on } \partial \Omega_{\mathrm{a}}^{\mathrm{t}} \\
\boldsymbol{u}=\overline{\boldsymbol{u}} & \quad \text { on } \partial \Omega_{\mathrm{u}}^{\mathrm{t}}
\end{aligned}
$$

が初期配置に引き戻されると次のようになります。
$$
\begin{array}{r}
\boldsymbol{\nabla}_{\boldsymbol{X}} \cdot\left(\left(\boldsymbol{I}+\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right) \boldsymbol{S}\right)^{T}+\mathbf{f}_{V}^{0}=\mathbf{0} \\ \boldsymbol{S}=\mathbb{C}: \boldsymbol{E} \quad \text { in } \Omega_{0} \\
\boldsymbol{E}=\frac{1}{2}\left[\left(\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right)^{T}+\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}+\left(\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right)^{T} \boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right] \quad \text { in } \Omega_{0} \\
\left(\boldsymbol{I}+\boldsymbol{\nabla}_{\boldsymbol{X}} \boldsymbol{u}\right) \boldsymbol{S} \cdot \boldsymbol{N}=\mathbf{f}_{\boldsymbol{A}}^{0} \quad \text { on } \partial \Omega_{\mathrm{A}}^{0} \\
\boldsymbol{u}=\overline{\boldsymbol{u}} \quad \text { on } \partial \Omega_{\mathbf{u}}^{0}
\end{array}
$$

　問題を初期配置上に書き直すと、非線形項の存在がより見えやすくなりました（図中の赤字部分が幾何学的非線形にと関係する項です）。比較するため、幾何学的線形を選んだ場合の支配方程式を以下に示します。幾何学的線形かつ材料線形の仮定では、支配方程式に非線形項が全く現れないこ とがもう一度確認できます。
$$
\begin{array}{r}
\boldsymbol{\nabla} \cdot \boldsymbol{\sigma}+\mathbf{f}_{v}=\mathbf{0} \quad \text { in } \Omega \\ \boldsymbol{\sigma}=\boldsymbol{C}: \boldsymbol{\varepsilon} \quad \text { in } \Omega \\ \boldsymbol{\varepsilon}=\frac{1}{2}\left[(\boldsymbol{\nabla} \boldsymbol{u})^{T}+\boldsymbol{\nabla} \boldsymbol{u}\right] \quad \text { in } \Omega \\ \boldsymbol{\sigma} \cdot \boldsymbol{n}=\mathbf{f}_{a} \quad \text { on } \partial \Omega_{\mathrm{a}} \\
\boldsymbol{u}=\overline{\boldsymbol{u}} \quad \text { on } \partial \Omega_{\mathbf{u}}
\end{array}
$$

　非線形項の出現により方程式の解を求めることが難しくなり、非線形性が強くなるほど収束が難しくな ります。一般には幾何学的非線形に加えて材料非線形（超弾性や弾塑性など）、さらには接触（境界条件の非線形）などを同時に扱うことも多く、いつそう難度が上がります。次回の記事では「幾何学的非線形のみ（材料線形•死荷重条件）」に絞り、弱形式の非線形項およびその非線形項が求解に与 える影響について確認します。

著者

張広志 Ph．D．
計測エンジニアリングシステム株式会社 技術部
非線形性固体力学•非線形有限要素法ならびに、COMSOL Multiphysics ${ }^{\circledR}$ への技術サポートに従事
計算力学技術者 固体力学分野1級 振動分野1級