モノづくりと不確かさの定量化(第3回)回帰モデルの導入

3 回帰モデルの導入
前回までに、設計プロセスにおける不確かさ(バラツキ)を定量化するために有用な代理モデル(Emulator)を紹介した。
代理モデルを抽象化すると、設計条件を入力とし、数値化された性能・機能を出力(目的変数)とする関数(写像)となり、設計対象の振舞いを関数で表現することになる。入力を\(\ D\ \)次元のベクトル \({\bf x}\) 、スカラーである出力を\(\ y\ \) と表すこととし、\(\ n\ \) 個の観測値 \[{\cal D}=\{\,({\bf x}_i,y_i)\,|\,i=1,\cdots ,n\,\} \tag{3.1}\]が学習データとして与えられたときに、学習データには含まれない新たな入力\(\ {\bf x}_*\ \) から出力を予測・推定する帰納的学習モデルである。機械学習の分野では、出力が離散値の場合には分類モデル、連続値の場合には回帰モデルと位置付けられるが、これ以降は回帰モデルの場合に、未知の関数についてどのような制約を想定することができるのかを考えることとし、入出力の間にわずかな誤差\(\ \epsilon\ \)を仮定する。 \[y=f({\bf x})+\epsilon\tag{3.2}\]
3.1 最も単純な回帰モデルと最小二乗法
入力が1次元の場合を考え、関数として1次式 \[f(x)=w_1x+w_2 \tag{3.3}\] を想定する。このモデルはパラメータ \({\bf w}=(w_1,w_2 )\) で定まる直線である。式 (3.1) の観測値が与えられたときに、関数モデル\(\ f(x_i )\ \)と\(\ y_i\ \)の誤差の平方和\(\ \varDelta\ \)が最小となるようにパラメータ\(\ {\bf w}=(w_1,w_2)\ \)を求めるのが最小二乗法である。 \[\varDelta=\sum_{i=1}^{n} \left(\,y_i-f(x_i)\,\right)^2 \tag{3.4}\] 例として、図 3.1 の左側に示すデータ空間では、赤色の観測値から最小二乗法で得られる関数\(\ f(x)\ \)は青色の直線となる。一方、右側に示すパラメータ空間では、赤色の x 印で表される。データ空間における複数の観測値から求められた直線とパラメータ空間内の1点が対応すると考えることができる。データ空間では、観測値\(\ y_i\ \)と関数モデルの出力\(\ f(x_i )\ \)の差が観測ノイズ\(\ \epsilon\ \)として発生していると見做すことができる。
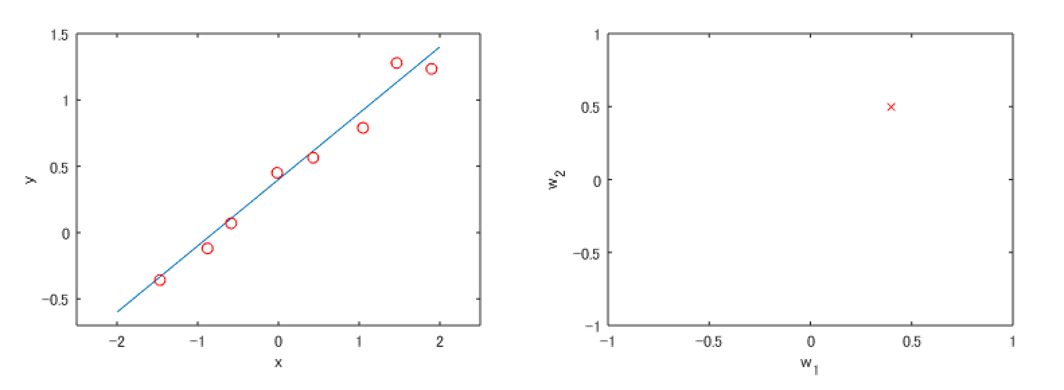
(左)データ空間、(右)パラメータ空間
3.2 最も単純なモデルと確率モデル
図 3.1(左)で観測される誤差\(\ \epsilon\ \)は、確率変数と見做せるが、ここではパラメータ空間でのバラツキを確率変数として捉えると、どのような確率モデルが導かれるのかを定性的に示す。
関数として式 (3.3) の一次式を想定した時点では、パラメータ\(\ {\bf w}\ \)の値は確定していないため、\(\ {\bf w}\ \)で決まる点は図 3.2(右上)のように空間全体に分布していて、霧のような確率分布\(\ p({\bf w})\ \)を仮定することができる。この霧の中から赤色のx印で示す標本(サンプル)をランダムに抽出すると、図 3.2(左上)に示すようにパラメータの標本値に対応する直線群が得られる。
ここで、学習データ\(\ {\cal D}\ \)が与えられると、霧は図 3.1(右)の点の周辺に集中した局所的な雲のように変化する(図 3.2(右下))。この雲の中からランダムに抽出した15個の標本値に対応する直線を求めると図 3.2(左下)が得られる。図 3.1(左)のような一本の直線ではなく、学習データが与えられたときにどの程度の信頼度をもって予測ができるが示すことができることが示唆される。
学習データ\(\ {\cal D}\ \)が与えられる前後でのパラメータ\(\ {\bf w}\ \)の確率分布をそれぞれ事前分布(prior distribution)、事後分布(posterior distribution)といいい、確率分布\(\ p({\bf w})\ \)と条件付き確率分布\(\ p({\bf w}\,|\,{\cal D})\ \)で表す。
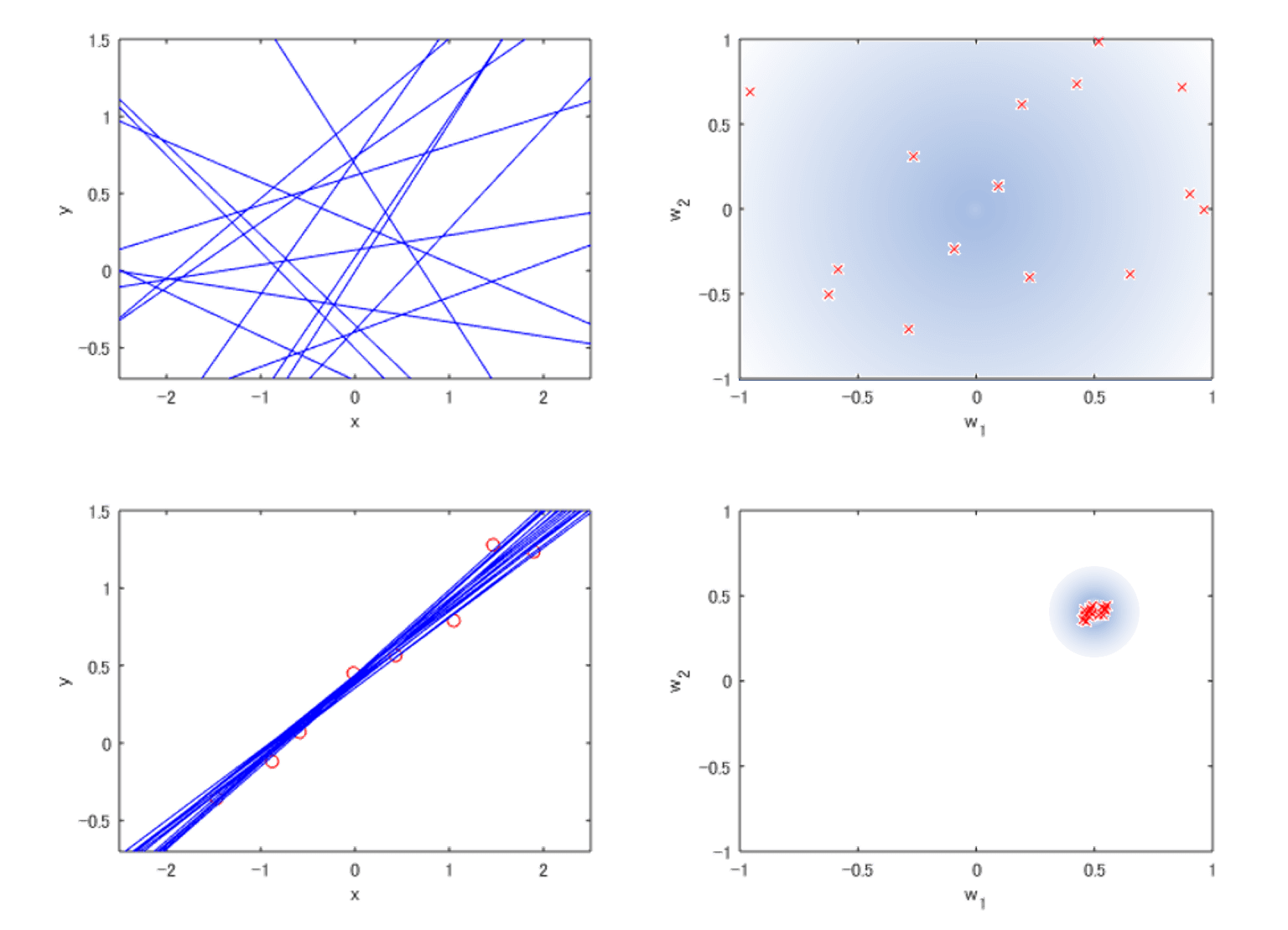
(右上)事前分布\(\ p({\bf w})\ \)、(右下)事後分布\(\ p({\bf w}\, |\,{\cal D})\ \)
3.3 単回帰モデルからの拡張シナリオ
これまで考えてきたモデルは、式 (3.3) で示される単回帰(simple regression)モデルであり、入力変数の次元を1次元に限定、また直線で近似できるモデルに限定してきた。この制約の強い単回帰モデルから普遍的な回帰モデルへ拡張するシナリオを次回以降展開する。
まず次元\(\ D\ \)の拡張によって重回帰(multiple regression)モデル、さらに基底関数選択の自由度を拡張することによって線形回帰(linear regression)モデルを導出する。
●モノづくりと不確かさの定量化(第2回)
https://kesco.co.jp/blog/3092/
●モノづくりと不確かさの定量化(第1回)
https://kesco.co.jp/blog/539/